新课标高二试卷(1)(必修3与选修2-1)
一、填空题:(本大题共14题,每小题5分,共70分)
1、命题“![]() ”的否定是_________________(要求用数学符号表示).
”的否定是_________________(要求用数学符号表示).
2、已知P: 2x-3 >1;q:,则┐p是┐q的__________条件.
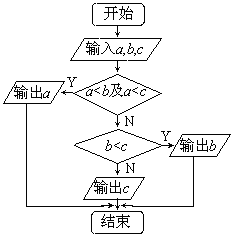
3、阅读下面的流程图:
则此流程图所表示的意义为: 算法.
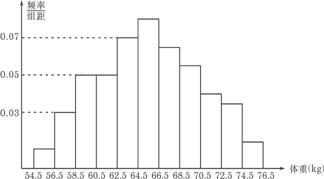
4、为了了解某地区高三学生身体发育情况,抽查了该地区100名年龄为17.5岁~18岁的男生体重(kg) ,得到频率分布直方图,如图.根据上图可得这100名学生中体重在〔56.5,64.5〕的学生人数是 .
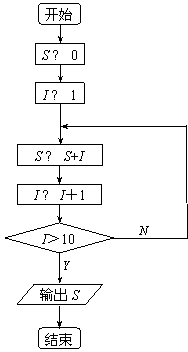
5、采用简单随机抽样从含10个个体的总体中抽取一个容量为4的样本,个体a前两次未被抽到,第三次被抽到的概率为_____________________.
6、一艘轮船只有在涨潮的时候才能驶入港口,已知该港口每天涨潮的时间为早晨5:00至7:00和下午5:00至6:00,则该船在一昼夜内可以进港的概率是 .
7、已知x、y之间的一组数据如下:
| x | 0 | 1 | 2 | 3 |
| y | 8 | 2 | 6 | 4 |
则线性回归方程![]() 所表示的直线必经过点_____________.
所表示的直线必经过点_____________.
8、 x←5
y←-20
IF x<0 THEN
x←y-3
ELSE
y←y+3
END IF
![]()
PRINT ![]()
运行后输出的结果为__ .
9、椭圆的两个焦点和短轴两个顶点,是一个含60°角的菱形的四个顶点,则椭圆的离心率为____________.
10、已知椭圆的长轴、短轴、焦距长度之和为8,则长半轴的最小值是_________.
11、已知双曲线的两条准线将两焦点间的线段三等分,则双曲线的离心率是______________.
12、平面内,动点![]() 到定点
到定点![]() 的距离等于到定直线
的距离等于到定直线![]() 的距离的轨迹是
的距离的轨迹是
__________________(只要填出轨迹的形状).
13、已知![]() 是抛物线
是抛物线![]() 上的一点,
上的一点,![]() 是平面内的一定点,
是平面内的一定点,![]() 是抛物线的焦点,当
是抛物线的焦点,当![]() 点坐标是__________时,
点坐标是__________时,![]() 最小.
最小.
14、以下四个关于圆锥曲线的命题中:
①设A、B为两个定点,k为非零常数,![]() ,则动点P的轨迹为双曲线;
,则动点P的轨迹为双曲线;
②以定点A为焦点,定直线l为准线的椭圆(A不在l上)有无数多个;
③方程![]() 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率;
④过原点O任做一直线,若与抛物线![]() ,
,![]() 分别交于A、B两点,则
分别交于A、B两点,则![]() 为定值.
为定值.
其中真命题的序号为 ___________(写出所有真命题的序号).
二、解答题:(本大题共6小题,共90分)
15、(本小题14分,每问7分)
将下列问题的算法用伪代码中的“for”语句表示(写在下面的框中),并画出流程图.
 |  | ||
16、(本小题14分,每问7分)
等腰![]() 中,
中,![]() .
.
(1)在线段![]() 上任取一点
上任取一点![]() ,求使
,求使![]() 的概率;
的概率;
(2)在![]() 内任作射线
内任作射线![]() ,求使
,求使![]() 的概率.
的概率.
17、(本小题15分,每问5分)
从数字1,2,3,4,5中任取2个数,组成没有重复数字的两位数,试求:
(1)这个两位数是5的倍数的概率;
(2)这个两位数是偶数的概率;
(3)若题目改为“从1,2,3,4,5中任取3个数,组成没有重复数字的三位数”,则这个三位数大于234的概率.
(要求写出必要的解题过程,只写答案得零分)
18、(本小题14分,每问7分)
已知双曲线的中心在原点,焦点![]() 在坐标轴上,一条渐近线方程为
在坐标轴上,一条渐近线方程为![]() ,且过点
,且过点![]() .
.
(1) 求双曲线方程;
(2)
若点![]() 在此双曲线上,求
在此双曲线上,求![]() .
.
19、(本小题15分,第一问7分,第二问8分)
已知抛物线![]() ,
,
(1)若![]() ,设
,设![]() 点坐标为
点坐标为![]() ,求抛物线上距点
,求抛物线上距点![]() 最近的点
最近的点![]() 的坐标及相应的距离
的坐标及相应的距离![]() ;
;
(2)若![]() 到抛物线上点的最小距离为4,求抛物线的方程.
到抛物线上点的最小距离为4,求抛物线的方程.
20、(本小题18分,每问6分)
已知直线![]() ,椭圆
,椭圆![]() ,
,
(1)过点![]() (
(![]() ,
,![]() )且被
)且被![]() 点平分的弦所在直线的方程;
点平分的弦所在直线的方程;
(2)![]() 是椭圆
是椭圆![]() 上的一点,
上的一点,![]() 是椭圆
是椭圆![]() 的两个焦点,当
的两个焦点,当![]() 在何位置时,
在何位置时,![]() 最大,并说明理由;
最大,并说明理由;
(3)求与椭圆![]() 有公共焦点,与直线
有公共焦点,与直线![]() 有公共点,且长轴长最小的椭圆方程.
有公共点,且长轴长最小的椭圆方程.
参考答案及评分标准
一、填空题:
1、![]() 2、充分不必要
3、求三个数中最小数 4、40 5、
2、充分不必要
3、求三个数中最小数 4、40 5、![]() 6、
6、![]()
7、![]() 8、22 9、
8、22 9、![]() 或
或![]() (注:只答一个得3分) 10、
(注:只答一个得3分) 10、![]()
11、![]() 12、直线
13、
12、直线
13、![]() 14、②③④
14、②③④
 二、解答题:
二、解答题:
15、解:

(伪代码)
7分
14分
16、解:(1)设![]() ,则
,则![]() (不妨设
(不妨设![]() ).若
).若![]() ,
,
则![]() ,故
,故![]() 的概率,
的概率,
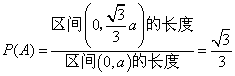 7分
7分
(2)设![]() ,则
,则![]() .若
.若![]() ,
,
则![]() ,故
,故![]() 的概率
的概率![]() 14分
14分
17、解:(1)设“两位数是5的倍数”为事件![]() ,
,
则![]() 4分
4分
答:这个两位数是5的倍数的概率为![]() .
5分
.
5分
(2)设“两位数是偶数”为事件![]() ,
,
则![]() 9分
9分
答:这个两位数是偶数的概率为![]() .
10分
.
10分
(3)设“三位数大于234”为事件![]() ,
,
则![]() 14分
14分
答:三位数大于234的概率为![]() .
15分
.
15分
18、解:(1)由题意,设双曲线方程为![]() 2分
2分
将点![]() 代入双曲线方程,得
代入双曲线方程,得![]() ,
,
即![]() 5分
5分
所以,所求的双曲线方程为![]() 7分
7分
(2)由(1)知![]()
因为![]() ,所以
,所以![]() 9分
9分
又![]() 在双曲线
在双曲线![]() 上,则
上,则![]() 11分
11分
![]() 14分
14分
19、解:设![]() 上任一点
上任一点![]() ,则
,则
![]()
(1)当![]() 时,
时,![]() 3分
3分
所以当![]() 时,
时,![]() 5分
5分
所以![]() ,此时
,此时![]() 7分
7分
(2)当![]() 时,
时,![]() 9分
9分
当![]() 时,
时,![]() 时,取得最小值为
时,取得最小值为![]() 11分
11分
当![]() 时,
时,![]() 时取得最小值为
时取得最小值为![]() 13分
13分
解得![]() 或
或![]() (舍),所以抛物线方程为
(舍),所以抛物线方程为![]() .
15分
.
15分
20、解:(1)设以![]() 为中点的弦的端点为A(
为中点的弦的端点为A(![]() ),B(
),B(![]() ),
),
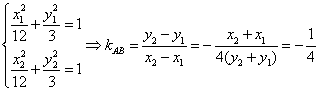 4分
4分
所以直线![]() 的方程为
的方程为![]() 即
即![]() 6分
6分
(2)设![]() ,则
,则![]()
![]() 9分
9分
又![]() (当且仅当
(当且仅当![]() 时取等号)
时取等号)
所以当![]() 即
即![]() 时,
时,![]() 最小
11分
最小
11分
又![]() ,所以当
,所以当![]() 为短轴端点时,
为短轴端点时,![]() 最大
12分
最大
12分
(3)因为![]() ,所以
,所以![]() .
13分
.
13分
则由题意,设所求的椭圆方程为![]() ,
,
将![]() 代入上述椭圆方程,消去
代入上述椭圆方程,消去![]() ,得
,得![]() ,
,
依题意![]() ,
15分
,
15分
化简得![]() ,
17分
,
17分
因为![]() ,所以
,所以![]() ,故所求的椭圆方程为
,故所求的椭圆方程为![]() 18分
18分
[另解]由题意,得所求椭圆的两焦点分别为![]() ,则
,则![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,设所求椭圆与直线
,设所求椭圆与直线![]() 的交点为
的交点为![]() ,则
,则
![]() ,(当且仅当
,(当且仅当![]() 共线时取等号)
共线时取等号)
所以![]() ,又
,又![]() ,
,
故所求的椭圆方程为![]()
(若有不同解法,请相应给分)