高二数学期末考试卷（必修3，选修1-1）
一、选择题（本大题共10小题，每小题5分，计50分，每小题有四个选项，其中只有一项是符合题意的，请把你认为正确的项选出，填在答题纸的相应位置）
1．从总数为N的一批零件中抽取一个容量为30的样本，若每个零件被抽取的概率为0.25，则N等于
A．200 B．
2．将长为
的木棍随机分成两段，则两段长都大于
的概率为
A．
B．
C．
D．
3．设p∶
∶
0，则p是q的
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要条件
4．已知△ABC的顶点B、C在椭圆＋y2＝1上，顶点A是椭圆的一个焦点，且椭圆的另外一个焦点在BC边上，则△ABC的周长是
A．2 B．6
C．4 D．12
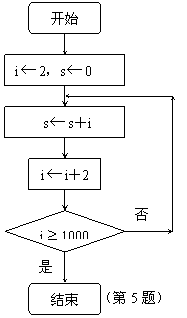
5．给出下面的程序框图，那么其循环体执行的次数是
A．500 B．499
C． 1000 D．998
6．下列命题是真命题的是
A．
B．
C．
D．
7．为了考察两个变量x和y之间的线性相关性，甲、乙两位同学各自独立地做10次和15次试验，并且利用线性回归方法，求得回归直线分别为l1和l2，已知两个人在试验中发现对变量x的观测数据的平均值都是s，对变量y的观测数据的平均值都是t，那么下列说法正确的是
A．l1和l2有交点（s，t） B．l1与l2相交，但交点不一定是（s，t）
C．l1与l2必定平行 D．l1与l2必定重合
8．下列说法正确的是
A．x2 = y2
x = y B．等比数列是递增数列的一个必要条件是公比大于1.
C．命题“若
，则
”的逆命题是真命题 D．若a
+ b>3，则a>1或b＞2.
9．在一个口袋中装有4个白球和2个黑球，这些球除颜色外完全相同，从中摸出2 个球，至少摸到1个黑球的概率等于
A．
B．
C．
D．
10．椭圆
的左、右焦点分别为
，点
在椭圆上，若
是一个直角三角形的三个顶点，则点到
轴的距离为
A．
B．
C．或 D．以上均不对
二、填空题（本大题共6小题，每小题5分，计30分，请把你认为正确的答案填在答题纸的相应位置）
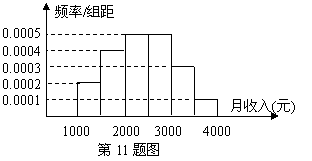
11．一个社会调查机构就某地居民的月收入调查了10 000人，并根据所得数据画了样本的频率分布直方图（如下图）．为了分析居民的收入与年龄、学历、职业等方面的关系，要从这10 000人中再用分层抽样方法抽出100人作进一步调查，则在［2500，3000）（元）月收入段应抽出
人．
 |
12．命题“"x∈R，x2－x+3>
13．阅读右上框中伪代码，若输入的n值是50，则输出的结果是 ．
14．方程
表示椭圆的充要条件是
．
15．某人5次上班途中所花的时间（单位：分钟）分别为x，y，10，11，9.已知这组数据的平均数为10，方差为2，则｜x－y｜的值为 ．
16．在区间[1,5]和[2,4]分别各取一个数，记为m和n，则方程
表示焦点在x轴上的椭圆的概率是
．
三、解答题（本大题共6题，计80分，请在题后空白处写出相应的解答过程）
17．（本题满分12分）
张三卖鸡50天，每天卖鸡的数可用茎叶图表示如下：
| 1 | 3 4 5 6 6 6 7 8 8 8 8 9 9 9 |
| 2 | 0 0 0 0 1 1 2 2 2 2 2 3 3 3 3 4 4 5 5 5 6 6 6 6 7 7 7 8 8 8 9 |
| 3 | 0 1 1 2 3 |
将其分成7组：
⑴填频率分布表，并回答卖鸡数从25只到30只的频率是多少？
⑵在同一坐标系中，画出频率分布直方图和折线图．
频率分布表
| 分组 | 频数 |
|
|
| ||
| 合计 |
频率
|
已知算法：（1）指出其功能（用算式表示），
（2）将该算法用流程图描述之。
19．（本小题满分14分）已知在平面直角坐标系
中的一个椭圆，它的中心在原点，左焦点为
,右顶点为
,设点
.
⑴求该椭圆的标准方程；
⑵若是椭圆上的动点，求线段
中点
的轨迹方程
20．（本小题满分14分）已知P：2x2-9x+a
< 0,q：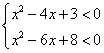
且
p是q的充分条件,求实数a的取值范围.
21．（本小题满分14分）袋中装有35个球，每个球上都记有从1到35的一个号码，设号码为
的球的重量为
(克)，这些球以等可能性(不受重量、号码的影响)从袋中取出。⑴如果任意取出1球，试求其重量大于号码数的概率；⑵如果同时任意取出2球，试求它们重量相同的概率.
22．（本小题满分14分）将圆O：
上各点纵坐标缩短到原来的一半，（横坐标不变），得到曲线C．
⑴求曲线C的方程；
⑵设O为坐标原点，过点
的直线
与C交于
两点，
为
的中点，连结
并延长交曲线C于点E，
求证：
的充要条件是
.