典型例题一
例1 正六棱锥的底面周长为24，侧面与底面所成角为
，求：（1）棱锥的高；（2）斜高；（3）侧棱长；（4）侧棱与底面所成角．
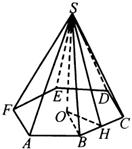分析：本题涉及了正棱锥的若干基本量，可以把基本量放置到直角三角形中，由已知量求未知量．
解：正六棱锥的底面周长为24．
∴正六棱锥的底面边长为4．
在正棱锥
中，
取
中点
，连
，
，
是正六边形
的中心．
连
，则
底面
∴
．
∴
是侧面与底面所成二面角的平面角，即
．
（1）在
△
中，
，，
∴
．
（2）同样在△中，斜高
，
（3）△中，
，
．
∴
．
（4）∵底面，∴
是侧棱与底面所成角，
同样在△
中，
，∴
，
说明：在立体几何中，要善于把长度和角度放到三角形中去解决，正棱锥中有关长度、角度主要在两上重要的直角三角形中，本题中的方法也可用于其它正棱锥中．比如：已知正四棱锥底面边长为
，相邻两侧面所成二面角为
，求正棱锥的高、斜高、侧棱长．正四棱锥相邻侧面是全等的等腰三角形，利用这个性质先落实相邻侧面所成二面的平面角，先计算侧棱长为
，然后利用底面边长和侧棱长在两个重要的直角三角形中，计算出高为
，斜高为
．
典型例题二
例2 如图所示，正四棱锥
棱长均为13，
，
分别是
，
上的点，且
．
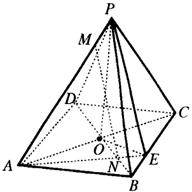（1）求证：直线
平面
；
（2）求直线
与底面
所成角的正弦．
分析：（1）要证明平面，只需证明与平面内某一条直线平行．为此连
并延长交于
，连
．可考虑证明
．（2）若能证明，则
即为直线与底面所成的角．
解：（1）连并延长交于，再连．
∵
，∴
，
又
，
∴
，
∴
，
又
平面，
平面，∴平面．
（2）设为底面中心，连
，
，则
平面．又，则为直线与平面
所成的角．
由
及
，得
，在△
中，
，
，，由余弦定理，得
．在△
中，
，，则
．
说明：本题（2）若直接求与平面所成的角，计算就比较复杂，而平移为求与底面所成的角，计算就易得多．可见，平移是求线线、线面所成角的重要方法．
典型例题三
例3 斜三棱柱
的底面△是直角三角形，
，侧棱与底面成角，点
在底面的射影
为的中点，
．
（1）求证
；
（2）若
为
的二面角，求四棱锥
的体积．
分析：证关键在于证出其中一条线垂直于另一条线所在的平面；而求棱锥的体积关键在于求出其底面积和高．这两个问题可由题设及线与线、线与面的位置关系求得．
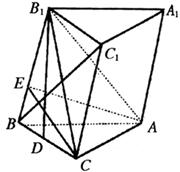解：如图所示，
（1）∵
平面，
底面，
∴
．
∵
，
∴
平面
，
∴
．
∵在底面上的射影为的中点，侧棱与底面成角，
∴四边形
是菱形，
∴
，
∴
平面
，
∴
．
（2）过
作
，连结
．
∵平面
，
∴
是在平面上的射影，
∴
，
∴
是二面角
的平面角，
∴
．
在△
中，
，在△
中，由
可得
．
∴
，
∴
．
∴ 
（体积单位）．
说明：证明线线垂直转化成证线面垂直是证明时常用的方法之一，而证线面垂直时又涉及线与线的垂直，因此线与面各种位置关系经常贯穿问题的始终．当遇到一线垂直于一截面，而截面面积又能计算时，将几何体分割成两个体积之和计算也是一种常用的方法．结果便转化成截面与此线相乘的关系，因而使问题得到简化．
典型例题四
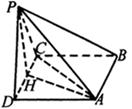
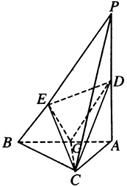例4如图，在三棱锥
中，
底面，
，、
分别是和
的中点，为
上一点，且
，
．
（1）求证：
平面
；
（2）求截面
分棱锥所成两部分的体积之比．
分析：由底面，可以判定平面
平面，且相交于，因为是的中点，且
，所以
，于是有
平面
，
．
若证平面，只需
与平面中的另一条直线垂直就可以了．为此，就要从已知的数量关系着手，找到新的线与线的垂直关系．
平面把三棱锥分成两部分，显然这两部分具有相同的高线
．所以，只要找到△
和四边形
的面积之比，就可以确定两部分的体积之比了．
证明：
（1）∵平面，且
平面
∴平面平面，且相交于
在△中，∵，是边上的中线
∴．∴平面
∵
平面，∴
利用两个平面垂直的性质定理可以证明平面
在△和△
中
设
，则
，
，
，
∵
，
∵
，∴△～△
∵
，∴
∴
．∵
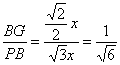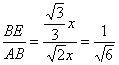
利用相似三角形的性质，得到
∴
∵
，∴平面．
解：（2）∵
∵
，
∴
∴
∴
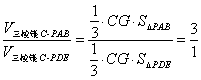
∴截面分棱锥为两部分，三棱锥
与四棱锥
的体积之比为1：2．
典型例题五
例5四棱锥，侧面
是边长为2的正三角形且与底面垂直，底面是面积为
的菱形，
为菱形的锐角．（1）求证：
；（2）求二面角
的大小；（3）求棱锥的侧面积与体积．
分析：取
中点，侧面
底面，从而可利用三垂线定理转化为证明
，线面垂直也为二面角平面角的落实创造了有利条件，棱锥的侧面积可通过抓侧面三角形的特殊性来解决．
证明：（1）取中点，连
、
，
∵△是等边三角形，∴
，
∵面底面，∴
底面，
∵等边△的边长为2，∴
∴菱形的边长为2，又菱形的面积是，
∴
，∴
，又是锐角，
∴
，∴△
是等边三角形，
∴
，在平面
上射影为
，∴．
解：（2）∵
，由（1）
，
，
∴
，
．
∴
是二面角的平面角，
在△
中
，
∴
，即二面角的大小为
．
（3）由（2）在△中，可得
，
在△中，，
，∴
，
，
在△
中，
，，可得
，
在△中，
，，可得
，
又正△边长为2，∴
，
∴
，
∵
，∴
．
说明：抓线面垂直关系是解决立体几何问题的关键，非特殊棱柱、棱锥的侧面积，往往要通过逐个计算每个侧面的面积相加而得到，这就需要分析每个侧面的具体特点，比如是否为矩形、直角三角形、等边三角形等．可以举一个类似的例子，四棱锥
的高为1，底面为菱形，侧面
和侧面
所成角为，且都垂直于底面，另两侧面与底面都成角，求棱锥的全面积．这里由相交平面与都与底面垂直得到
垂直于底面，利用
底面，一方面落实了棱锥的高为
，另一方面几个二面角的平面角都能方便地落实，四个侧面中，有两个是等腰三角形，有两个是直角三角形，通过计算可得，全面积为
．
典型例题六
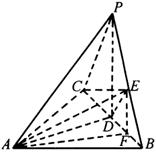例6 已知三棱锥中，、、
与底面所成角相等，
，
，为中点，点在上且
截面
，（1）求与底面所成角；（2）求到平面的距离．
分析：由、、与底面所成角相等可得
点在面上射影为△的外心，由于△是直角三角形，可以得到
面，面可转化为
，是中点，找出到面的垂线落实
与面所成角．到面的距离可从两方面得到，一方面直接找到面的垂线，另一方面，用等积法可求点到面的距离．
解：（1）∵、、与底面成相等的角，设在面上射影为，则有
，
∴△
≌△
≌△
，
∴
且
，
∴是△的外心．
∵△是直角三角形，且是斜边的中点，
∴点和点重合，即面，
∵截面，过的平面与平面交于
，
∴
，∵是中点，∴是中点，
取中点
，则
，∴
平面，
∴
为与底面所成角．
∵
，∴
，
∵
且
，∴
．
又
，∴△
也是等腰直角三角形，
∴
，∴
，
在△
中，
，
∴
，即与平面所成角为
．
（2）方法一：∵平面，∴
．
又∵
，∴
平面，∴
．
由（1）△是直角三角形，
，∴
，
∵
，∴
，∴
平面．
∵
，∴
．
即到平面的距离为．
方法二：∵
，，∴平面，
∴
，又
，
．
∴
，
∵
，
，
设到面的距离为
，
∴
，∴
．
，即到平面的距离为．
典型例题七
例7 如图所示，在三棱锥
中，
底面，
，
垂直平分
，且分别交、于、，又
，
．求以为棱，以
和
为面的二面角的度数．
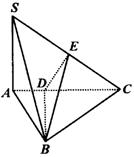
分析：从寻找二面角的平面角入手．二面角的平面角有时图形中没有给出，需要我们自己作出，有时平面角在图形中已经存在，只需要将其找出来．
解：∵平面，
平面，∴
．
∵是的垂直平分线，∴
，且是的中点．
又，∴
．
又
，∴平面，∴
．
又
，∴平面
，∴
，
．
从而
为二面角
的平面角．
设
，则
．
∵平面，∴
，
，从而
．
又，∴
．
在
中，
，∴
，
又，∴
．
因此所求的二面角的度数为
．
说明：本题是通过三棱锥来考查直线与直线、直线与平面、二面角、解三角形等知识，并考查了空间想像能力和逻辑推理能力．解答本题的关键是认定是二面角的平面角．这需要具有一定的观察能力和判断能力，而且要给出严格的证明．学生很可能发现不了即是所求二面角的平面角，自己再作二面角的平面角，使问题复杂化．本题所给条件较多，所以恰当地选择所需条件进行论证和计算也是解决本题的一个难点．
典型例题八
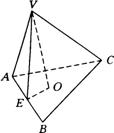
例8 是
所在平面外的一点，、、两两垂直，
．求到平面的距离．
分析：利用三棱锥的性质、体积以及线面关系求解．
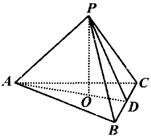
解法一：∵，∴在底面内的射影是的外心．又、、两两相互垂直，∴是等边三角形，∴是的重心．
如图，在
中，
，
∴
．
解法二：设点到平面的距离为．
∵、、两两垂直，，
∴
，
，
．
又
，
∴
，∴
．
∴到平面的距离为
．
解法三：取的中点，连
、
．
∵
，
，∴，
，
∴平面
，平面，
，
∴就是到平面
的距离．
在
中，，
，
．
又∵
，
∴
．
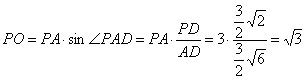说明：本题难度并不大．但是这里所给出的三种方法非常典型．方法一利用
确定在底面内射影为的外心；方法二利用体积转化的方法；方法三利用面面垂直的性质定理进行垂足定位．
典型例题九
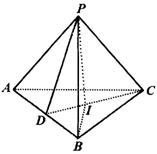
例9 如图所示，在三棱锥
中，底面为直角三角形，两直角边
，
三棱锥侧面与底面所成二面角都为．求此三棱锥的侧面积．
分析：本题可利用面积射影定理求解．若一棱锥各侧面与底面所成二面角都为
，且已知
，则由面积射影定理知：
．
解法一：过作底面的垂线，垂足为
，过在底面内作的垂线，垂足为，连结．由三垂线定理知
，∴
为侧面与底面所成二面角的平面角，即
．又可知为
的内心．∵，，
，从而
．在
中，由，得
，从而各侧面三角形的高均为
．
∴
．
解法二：
．
说明：本题考查了三棱锥的有关概念与性质．在三棱锥中，过一条侧棱和高的截面有许多重要性质，而这个截面又把棱锥的许多有线段、高、角都集中到同一个平面内，所以常常通过研究这个辅助平面来解决问题．解法二是求棱锥侧面积的一种简捷解法，用到了面积射影定理．
典型例题十
例10 三棱锥中，
，
．将此三棱锥沿三条侧棱剪开，其展开图是一个直角梯形
．如图所示．
(1)求证：侧棱
；
(2)求侧面
与底面所成的角
的余弦值．
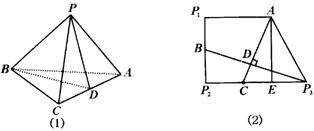
分析：(1)折叠与展开是互逆过程，将直角梯形折成三棱锥时，
，
的关系不变，于是在三棱锥中有
，故
，从而．
(2)由(1)可知，∴在平面内作
于，连，则
即是所求二面角的平面角，且
为
，∴只需求出两条边即可．而边长可以考虑在侧面展开图中求解．
证明：(1)见上述思路分析．
解：(2)作，则由三垂线定理知
，于是是二面角
的平面角，即
．再作
于，则
，且是
的中点，设
，
．在
中，
．且由
，得
，解得
，
．
由
，得
．
由，
，
，知
．
∴所求二面角的余弦值为
．
说明：折与展是一对互逆的过程．在处理这类问题时应充分注意折叠或展开前后各元素(主要是直线、线段、角)的相对位置和数量变化，注意哪些发生了变化，哪些不变．一般来说，位于同一半平面内的元素相对位置和数量关系不变．位于两个不同半平面内的元素，位置和数量要发生变化．这类问题常用的添辅助线方法是作棱的垂线．
典型例题十二
例12 下列命题中，真命题的个数是（ ）．
(1)两相邻侧棱所成之角相等的棱锥是正棱锥．
(2)两相邻侧面所成之角相等的棱锥是正棱锥．
(3)侧棱与底面所成之角相等的棱锥是正棱锥．
(4)侧面与底面所成之角相等的棱锥是正棱锥．
A．3个 B．2个 C．1个 D．0个
分析：有些同学错解的原因在于未能很好地理解正棱锥的定义以及正棱锥的性质，正棱锥的定义不同于正棱锥的性质，正棱锥的性质可以由其定义结合有关知识推导得到．
对照定义，构造反例．
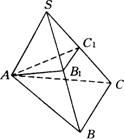
如图所示，是正三棱锥，两相邻侧棱所成之角相等，两相邻侧面所成之角相等．在
、上分别取异于
、的点、
，连
、
，则三棱锥
均满足命题(1)、(2)的条件，但显然不是正三棱锥，所以命题(1)、(2)为假命题．命题(3)中，侧棱与底面所成之角相等，顶点在底面的射影是底面多边形的外心．外心不一定是中心，因为底面不一定是正多边形，因此命题(3)也是假命题．在命题(4)中，侧面与底面所成之角相等，顶点在底面的射影是底面多边形的内心，而内心不一定是中心，所以命题(4)也是假命题．
综上可知应选D．
典型例题十三
例13 .如图，已知三棱锥中，，在底面上的射影为．
求证：为的外心．
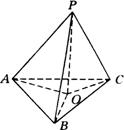
证明：连结、
、
、
，则底面
∵（斜线相等），
∴
（射影相等），
∴为的外心．
说明：(1)同理可证，如果三棱锥的三条侧棱与底面所成的角相等，那么顶点在底面上的射影也是底面三角形的外心．
(2)上述两结论对一般棱锥也成立，即棱锥的侧棱均相等或侧棱与底面所成的角均相等，则顶点在底面上的射影为底面多边形的外心．
典型例题十四
例14 如果三棱锥的三个侧面与底面所成的二面角都相等，那么顶点在底面上的射影为底面三角形的内心．
如图，已知三棱锥，三侧面、、与底面所成二面角都相等，点在底面上的射影为．求证：为的内心．
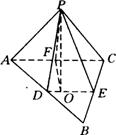
证明：连结，则平面．
在底面上作
、
、
，垂足分别为、、．
连结、、
．
由三垂线定理可得、
、
．
∴
、、
分别为二面角
，
，的平面角．
又∵
，
，
∴
≌
≌
，∴
，
∴为的内心．
说明：(1)同理可证，如果三棱锥的顶点到底面三条边的距离相等，那么顶点在底面上的射影为底面三角形的内心（若射影点在多边形内部的话）．
(2)上述两结论对一般棱锥也成立，即棱锥的各侧面与底面所成之角均相等或棱锥的顶点到底面各边距离相等，则顶点在底面上的射影为底面多边形内切圆的圆心（射影在多边形内部）．
(3)不要误论为棱锥顶点在底面上的射影一定在底面多边形的内部，顶点在底面的射影可以在底面多边形的外部，也可以在多边形的一边上．
典型例题十五
例15 如果三棱锥的三条侧棱两两垂直，那么顶点在底面上的射影是底面三角形的垂心．
已知三棱锥的三条侧棱、、两两垂直，为在底面上的射影．
求证：为底面三角形的垂心．
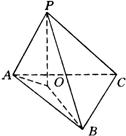
证明：如图，连结、
、
．
∵
，
，且
，
∴平面．
∴
．
又平面，
由三垂线定理的逆定理知，
．
同理，
．
∴点为的垂心．
说明：同理可证：如果三棱锥有两组对棱垂直，那么第三组对棱也垂直且顶点在底面上的射影为底面三角形的垂心．
典型例题十六
例16 三棱锥
的各面积分别为
，
，
，
，且各侧面与底面所成的二面角都相等，求侧面与底面所成二面角的平面角．
分析：首先找出二面角的平面角，转化到平面中去，然后利用已知条件列有关的等式．
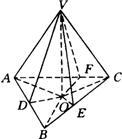
解：如图，作
平面于，连结、、
．
∵侧面与底面所成的角都相等，设者为，
∴为底面的内心，
∴过在底面内作，，，
垂足分别为、、；连结、
、
．
由三垂线定理可得
，
，
．
∴
．
∵
，
，而
，
∴
，∴
．
同理
，
，
∴
，
即
．
∴
，
∴
，∴
．
∴侧面与底面所成的二面角为
．
说明：(1)根据本题的推导过程不难得出如下结论：如果三棱锥的三个侧面与底面成等角，三棱锥的底面积为，侧面积为
，那么
．
(2)可以进一步证明：如果棱锥的各个侧面与底面成等角，那么．
典型例题十七
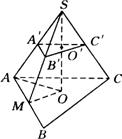
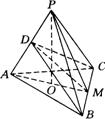
例17 如图，已知正三棱锥的高
，斜高
．求经过的中点平行于底面的截面
的面积．
分析：求出底面正三角形的边可得其面积，再利用棱锥截面性质，得截面面积．
解：连结
、．
在
中，
．
因为棱锥是正棱锥，所以点是正三角形的中心．
，
．
据一般棱锥截面的性质，有
．∴
．
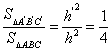说明：过高的中点且平行于底面的截面叫做中截面．
典型例题十八
例18 如图，已知棱锥的底面积是
，平行于底面的截面面积是
，棱锥顶点
在截面和底面上的射影分别是
、，过
的三等分点作平行于底面的截面，求各截面的面积．
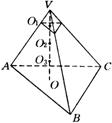
分析：顶点到已知截面的距离
与原棱锥高的关系，可由已知截面面积与底面积的量的关系得到，从而各截面对应的高与原棱锥的高的关系可以求出，再运用一般棱锥截面性质可以求得各截面面积．
解：设棱锥的高为，其顶点到已知截面之距
，
的三等分点为
、
，
由已知得
，∴
，∴
∴
，
而
，则
．
∴
，
．
设过、的截面面积分别为
、
，底面面积为
则
，∴
(
)．
，∴
()．
∴两截面的面积分别为
和
．
说明：本题还可以求得以为顶点，分别以过的截面、过的截面、过的截面为底面的棱锥，以及原棱锥的侧面积之比，这四个棱锥的侧面积之比依次为
．
典型例题十九
例19 正三棱锥底面边长和高都是4，它的一个内接三棱柱的三个侧面都是正方形．求内接三棱柱的全面积．
分析：如图所示．三棱柱的上底面
与正三棱锥的底面相似，它们的相似比等于
．设三棱柱的棱长为
，则有
，得出
，
．
解：设三棱柱的棱长为，由于三棱柱的上底面∽，则有
，即，∴，
，
，
∴
．
典型例题二十
例20 如图(1)设正三棱锥的底面边长，侧棱长为
，过
作与、分别交于和的截面，当截面
的周长最小时，求截面的面积．
分析：因为截面的三个顶点都在正三棱锥的侧面上，现若沿侧棱将棱锥展开，则截面的周长为最小时，就是线段
的长，如图(2)所示．
解：将正三棱锥沿侧棱展开，当截面的周长为最小值时，其周长即是展开图中线段之长．
在侧面展开图中，∵
，且
．
∴四边形
是等腰梯形，
，∴
，
∴
∽
，
．∵
，∴
．
∵
，又
，∴
．
∴
．
在三棱锥中，取截面的边的中点为，
∵
，∴
，∴
，
∴
．
说明：本例中，求侧面展开图中之长时运用了平面几何知识，过程较为简明．若在三角形
中，由
，计算出
的余弦后，再用余弦定理求之长，就麻烦得多了．
典型例题二十一
例21 已知正三棱锥的底面边长为，过作截面
垂直侧棱于，且此截面与底面成
的二面角，求此正三棱锥的侧面积．
分析：先找出二面角的平面角，再由正三棱锥的一些线面关系，把要求的斜高转化到直角三角形中，解直角三角形．
解：如图，作底面于．
∵为正三棱锥，
∴为底面正三角形的中心，连结交于，连结
，
则
，
，
∴平面
，
，
∴
为截面与底面所成二面角的平面角，
∴
．
∵平面，∴
，
．
∵正三角形的边长为，∴
，
．
在
中，
．
在
中，∵
，
∴
．
说明：(1)在多面体中，求边长、侧棱长、高和斜高等长度以及距离、角等等，要充分注意各多面体的概念，在多面体中首先画出所求元素，其次根据不同情况作出辅助线（注意经常用到三垂线定理），然后加以解决．
典型例题二十二
例22 棱锥的底面是等腰三角形，这等腰三角形的底边长为
，腰长为
，棱锥的侧面与底面所成的二面角都是
，求这个棱锥的侧面积．
已知三棱锥的底边是等腰三角形，
，
，侧面
、
、
与底面所成的二面角都是．
求棱锥的侧面积．
解法1：作点在底面上的射影，如图，
则是底面的内心，作
于点，连接，
则
（三垂线定理），故
是侧面与底面所成的二面角的平面角，
，
∵内切圆半径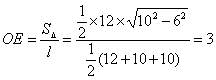
，
其中
，
是的面积．
∴斜高
，
∴
．
即棱锥的侧面积为
．
解法2：还可用面积射影定理：由于棱锥的侧面与底面所成的二面角均为，
故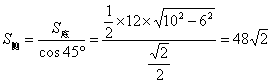
说明：(1)求棱锥侧面积，关键是求各个侧面三角形的高，即斜高，要熟悉三角形的面积公式．如
；
；
，
．
(2)在棱锥中，若侧棱相等或侧棱与底面的夹角相等，则该点在底面的射影是底面多边形的外心；若斜高相等或侧面与底面的夹角相等，则该点在底面的射影为底面多边形的内心．
典型例题二十三
例23 在四棱锥的四个侧面中，直角三角形最多可有（ ）．
A．1 B．2 C．3 D．4
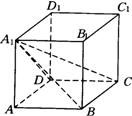
解：如图，在长方体
中，取四棱锥
，则此四棱锥的四个侧面都是直角三角形．
∴应选D．
说明：本题对给出的四棱锥没有带任何附加条件，只给出了思考、探索的方向，即思考、探索侧面为直角三角形的四棱锥应是怎样的模型，让人们展开充分的想象空间，让人们去思考、探索问题，确实是一道好题，也是今后命题的方向，对培养学生的能力大有裨益．