典型例题一
例1 若![]() ,
,![]() ,则
,则![]() ,
,![]() 的位置关系是(
).
的位置关系是(
).
A.异面直线 B.相交直线
C.平行直线 D.相交直线或异面直线
分析:判断两条直线的位置关系,可以通过观察满足已知条件的模型或图形而得出正确结论.
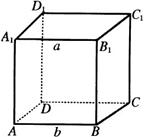
解:如图所示,在正方体![]() 中,设
中,设![]() ,
,![]() ,则
,则![]() .
.
若设![]() ,则
,则![]() 与
与![]() 相交.若设
相交.若设![]() ,则
,则![]() 与
与![]() 异面.
异面.
故选D.
 说明:利用具体模型或图形解决问题的方法既直观又易于理解.一般以正方体、四面体等为具体模型.例如,
说明:利用具体模型或图形解决问题的方法既直观又易于理解.一般以正方体、四面体等为具体模型.例如,![]() ,
,![]() 相交,
相交,![]() ,
,![]() 相交,则
相交,则![]() ,
,![]() 的位置关系是相交、平行或异面.类似地;
的位置关系是相交、平行或异面.类似地;![]() ,
,![]() 异面,
异面,![]() ,
,![]() 异面,则
异面,则![]() ,
,![]() 的位置关系是平行、相交或异面.这些都可以用正方体模型来判断.
的位置关系是平行、相交或异面.这些都可以用正方体模型来判断.
典型例题二
例2 已知直线![]() 和点
和点![]() ,
,![]() ,求证:过点
,求证:过点![]() 有且只有一条直线和
有且只有一条直线和![]() 平行.
平行.
分析:“有且只有”的含义表明既有又惟一,因而这里要证明的有两个方面,即存在性和惟一性.
存在性,即证明满足条件的对象是存在的,它常用构造法(即找到满足条件的对象来证明);惟一性,即证明满足条件的对象只有一个,换句话说,说是不存在第二个满足条件的对象.
因此,这是否定性命题,常用反证法.
证明:(1)存在性.
∵ ![]() ,∴
,∴ ![]() 和
和![]() 可确定一个平面
可确定一个平面![]() ,
,
由平面几何知识知,在![]() 内存在着过点
内存在着过点![]() 和
和![]() 平行的直线.
平行的直线.
(2)惟一性
假设在空间过点![]() 有两条直线
有两条直线![]() 和
和![]() 满足
满足![]() 和
和![]() .根据公理4,必有
.根据公理4,必有![]() 与
与![]() 矛盾,
矛盾,
∴ 过点![]() 有一条且只有一条直线和
有一条且只有一条直线和![]() 平行.
平行.
说明:对于证明“有且只有”这类问题,一定要注意证明它的存在性和惟一性.
典型例题三
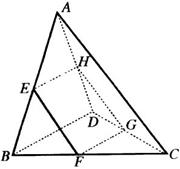 例3 如图所示,设
例3 如图所示,设![]() ,
,![]() ,
,![]() ,
,![]() 分别是空间四边形
分别是空间四边形![]() 的边
的边![]() ,
,![]() ,
,![]() ,
,![]() 上的点,且
上的点,且![]() ,
,![]() ,求证:
,求证:
(1)当![]() 时,四边形
时,四边形![]() 是平行四边形;
是平行四边形;
(2)当![]() 时,四边形
时,四边形![]() 是梯形.
是梯形.
分析:只需利用空间等角定理证明![]() 即可.
即可.
证明:连结![]() ,
,
在![]() 中,
中,![]() ,∴
,∴ ![]() ,且
,且![]() .
.
在![]() 中,
中,![]() ,∴
,∴ ![]() ,且
,且![]() .
.
∴ ![]() ,
,
∴ 顶点![]() ,
,![]() ,
,![]() ,
,![]() 在由
在由![]() 和
和![]() 确定的平面内.
确定的平面内.
(1)当![]() 时,
时,![]() ,故四边形
,故四边形![]() 为平行四边形;
为平行四边形;
(2)当![]() 时,
时,![]() ,故四边形
,故四边形![]() 是梯形.
是梯形.
说明:显然,课本第11页的例题就是本题(2)的特殊情况.
特别地,当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,![]() 是空间四边形各边中点,以它们为顶点的四边形是平行四边形.
是空间四边形各边中点,以它们为顶点的四边形是平行四边形.
如果再加上条件![]() ,这时,平行四边形
,这时,平行四边形![]() 是菱形.
是菱形.
典型例题四
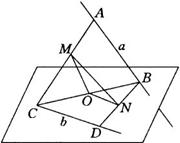 例4 已知
例4 已知![]() 是两条异面直线,直线
是两条异面直线,直线![]() 上的两点
上的两点![]() 的距离为6,直线
的距离为6,直线![]() 上的两点
上的两点![]() 的距离为8,
的距离为8,![]() 的中点分别为
的中点分别为![]() 且
且![]() ,求异面直线
,求异面直线![]() 所成的角.
所成的角.
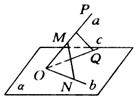
分析:解题的关键在于依据异面直线所成角的定义构造成和异面直线![]() 平行的两条相交直线,然后把它们归纳到某一三角形中求解.
平行的两条相交直线,然后把它们归纳到某一三角形中求解.
解:如图,连结![]() ,并取
,并取![]() 的中点
的中点![]() ,连结
,连结![]() ,
,
∵![]() 分别是
分别是![]() 和
和![]() 的中位线,
的中位线,
∴![]() ,
,![]() ,即
,即
![]() ,
,![]() .
.
∴![]() 所成的锐角或直角是异面直线
所成的锐角或直角是异面直线![]() 所成的角.
所成的角.
又∵ ![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
在![]() 中,又∵
中,又∵![]() ,
,
∴![]() ,
,
∴![]() .
.
故异面直线![]() 所成的角是
所成的角是![]() .
.
说明:在求两条异面直线所成的角时,一般要依据已知条件,找出与两条异面直线分别平行并且相交于一点的两条直线.但是,异面直线所成角的定义中的点![]() 一般是在图形中存在着的,需要认真观察分析图形的性质,从而找出这一点和过这一点与两异面直线平行的直线,以得到两条异面直线所成的角,在求这个角的大小时,一般是根据平面图形中解三角形的知识求解的.
一般是在图形中存在着的,需要认真观察分析图形的性质,从而找出这一点和过这一点与两异面直线平行的直线,以得到两条异面直线所成的角,在求这个角的大小时,一般是根据平面图形中解三角形的知识求解的.
典型例题五
例5 已知四面体![]() 的所有棱长均为
的所有棱长均为![]() .求:
.求:
(1)异面直线![]() 的公垂线段
的公垂线段![]() 及
及![]() 的长;
的长;
(2)异面直线![]() 和
和![]() 所成的角.
所成的角.
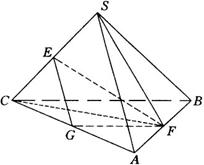 分析:依异面直线的公垂线的概念求作异面直线
分析:依异面直线的公垂线的概念求作异面直线![]() 的公垂线段,进而求出其距离;对于异面直线所成的角可采取平移构造法求解.
的公垂线段,进而求出其距离;对于异面直线所成的角可采取平移构造法求解.
解:(1)如图,分别取![]() 的中点
的中点![]() ,连结
,连结![]() .
.
由已知,得![]() ≌
≌![]() .
.
∴![]() ,
,![]() 是
是![]() 的中点,
的中点,
∴![]() .
.
同理可证![]()
∴![]() 是
是![]() 的公垂线段.
的公垂线段.
在![]() 中,
中,![]() ,
,![]() .
.
∴![]()
![]() .
.
(2)取![]() 的中点
的中点![]() ,连结
,连结![]() ,则
,则![]() .
.
∴![]() 和
和![]() 所成的锐角或直角就是异面直线
所成的锐角或直角就是异面直线![]() 和
和![]() 所成的角.
所成的角.
连结![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
由余弦定理,得
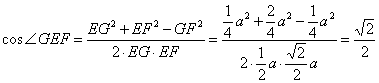 .
.
∴![]() .
.
故异面直线![]() 和
和![]() 所成的角为
所成的角为![]() .
.
说明:对于立体几何问题要注意转化为平面问题来解决,同时要将转化过程简要地写出来,然后再求值.
典型例题六
例6 如图所示,两个三角形![]() 和
和![]() 的对应顶点的连线
的对应顶点的连线![]() 、
、![]() 、
、![]() 交于同一点
交于同一点![]() ,且
,且![]() .
.
(1)证明:![]() ,
,![]() ,
,![]() ;
;
(2)求![]() 的值.
的值.
分析:证两线平等当然可用平面几何的方法.而求面积之比则需证两个三角形相似,由于三角形是平面图形,故也可用平面几何的方法证明.
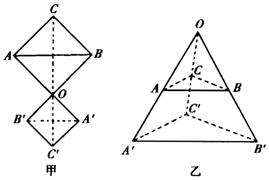
证明:(1)当![]() 和
和![]() 在
在![]() 点两侧时,如图甲
点两侧时,如图甲
∵![]() 与
与![]() 相交于
相交于![]() 点,且
点,且![]() ,
,
∴![]() (因为
(因为![]() 、
、![]() 共面).
共面).
同理![]() ,
,![]() .
.
(2)∵![]() ,且
,且![]() ,
,![]() 和
和![]() ,
,![]() 和
和![]() 的方向相反,∴
的方向相反,∴![]() ,同理
,同理![]() .
.
因此,![]() ∽
∽![]() .
.
又![]() ,∴
,∴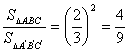 .
.
当![]() 和
和![]() 在
在![]() 点的同侧时,如图乙所示,同理可得(1)(2).
点的同侧时,如图乙所示,同理可得(1)(2).
说明:此题![]() 与
与![]() 是否共面并不重要,因为等角定理对各种位置已作说明.
是否共面并不重要,因为等角定理对各种位置已作说明.
典型例题七
例7 ![]() 是矩形
是矩形![]() 所在平面外一点,
所在平面外一点,![]() ,
,![]() ,
,![]() 与
与![]() 成
成![]() 角,
角,![]() 与
与![]() 成
成![]() 角,
角,![]() ,求:
,求:
(1)直线![]() 与
与![]() 的距离;
的距离;
(2)求直线![]() 与
与![]() 的距离.
的距离.
分析:要求出![]() 与
与![]() 、
、![]() 与
与![]() 的距离,必须找到它们的公垂线段,公垂线段的长度即为异面直线间的距离.
的距离,必须找到它们的公垂线段,公垂线段的长度即为异面直线间的距离.
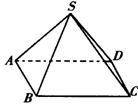
解:如图所示,在矩形![]() 中,
中,![]() .
.
∵![]() ,∴
,∴![]() .
.
又![]() ,∴
,∴![]() 是异面直线
是异面直线![]() 、
、![]() 的公垂线段,
的公垂线段,
其长度为异面直线![]() 、
、![]() 的距离.
的距离.
在![]() 中,∵
中,∵![]() 是
是![]() 与
与![]() 所成的角,
所成的角,
∴![]() .又
.又![]() ,∴
,∴![]() .
.
(2)在矩形![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,又
,又![]() ,
,
∴![]() 是直线
是直线![]() 、
、![]() 的公垂线段,其长度为异面直线
的公垂线段,其长度为异面直线![]() 、
、![]() 的距离.
的距离.
在![]() 中,
中,![]() 是异面直线
是异面直线![]() 与
与![]() 所成的角,∴
所成的角,∴![]() .
.
又![]() ,∴
,∴![]() ,
,
∴直线![]() 与
与![]() 的距离为
的距离为![]() .
.
说明:(1)求异面直线之间距离的步骤是:①找(作)线段;②证线段是公垂线段;③求公垂线段的长度.
(2)求异面直线间的距离的问题,高考中一般会给出公垂线段.
典型例题八
例8 ![]() 、
、![]() 、
、![]() 是三条直线,若
是三条直线,若![]() 与
与![]() 异面,
异面,![]() 与
与![]() 异面,判断
异面,判断![]() 与
与![]() 的位置关系,并画图说明.
的位置关系,并画图说明.
分析:这是一道考查异面直线概念及空间直线位置关系的问题,同时也考查了图形语言的表达能力.
解:直线![]() 与
与![]() 的位置关系有以下三种情形如图:
的位置关系有以下三种情形如图:
∴直线![]() 与
与![]() 的位置关系可能平行(图中的(1));可能相交(如图中的(2));
的位置关系可能平行(图中的(1));可能相交(如图中的(2));
可能异面(图中的(3)).
说明:本题也考查了空间想象能力和逻辑划分、分类讨论的能力.
典型例题九
例9 如果两条异面直线称作“一对”,那么在正方体的十二条棱中,共有几对异面直线( ).
A.12对 B.24对 C.36对 D.48对
分析:一般地,立体几何中的计数问题,是由所数的量的性质,确定一规律,然后按此规律进行计数.正方体的各棱具有相同的位置关系.所以以一条棱为基量,考察与其异面的几对,问题可解.
解:如图,正方体中与![]() 异面有
异面有![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∵各棱具有相同的位置关系,且正方体有12条棱,排除两棱的重复计算成本,
∴异面直线共有![]() 对.
对.
说明:分析清楚几何体特点是避免重复计数的关键.计数问题必须避免盲目乱数,做到“不重不漏”.
典型例题十
例10 如图,已知不共面的直线![]() ,
,![]() ,
,![]() 相交于
相交于![]() 点,
点,![]() 、
、![]() 是直线
是直线![]() 上两点,
上两点,![]() 、
、![]() 分别是
分别是![]() ,
,![]() 上一点.
上一点.
求证:![]() 和
和![]() 是异面直线.
是异面直线.
证法1:假设![]() 和
和![]() 不是异面直线,
不是异面直线,
则![]() 与
与![]() 在同一平面内,设为
在同一平面内,设为![]()
∵![]() ,
,![]()
∴![]() .
.
又![]() ,∴
,∴![]() .
.
∵![]() 且
且![]() ,
,![]() ,
,
∴![]() .
.
同理:![]()
∴![]() ,
,![]() ,
,![]() 共面于
共面于![]() ,与已知
,与已知![]() ,
,![]() ,
,![]() 不共面相矛盾,
不共面相矛盾,
∴![]() 、
、![]() 是异面直线.
是异面直线.
证法2:∵![]() ,∴直线
,∴直线![]() ,
,![]() 确定一平面设为
确定一平面设为![]() .
.
∵![]() ,
,![]() ,∴
,∴![]() ,
,![]() ,
,
∴![]() 且
且![]() ,
,![]() .
.
又![]() ,
,![]() ,
,![]() 不共面,
不共面,![]() ,∴
,∴![]() ,
,
∴![]() 与
与![]() 为异面直线.
为异面直线.
说明:证明两条直线异面的方法有两种.
(1)用定义证明(即定义法):此时需借反证法,假设两条直线不异面,根据空间两条直线的位置关系,这两条直线一定共面,即这两条直线可能相交也可能平行,然后,推导出矛盾即可.
(2)用定理证明(即定理法):用该法证明时,必须阐述出定理满足的条件:![]() ,
,![]() ,
,![]() ,然后可以推导出直线
,然后可以推导出直线![]() 与
与![]() 是异面直线.
是异面直线.
典型例题十一
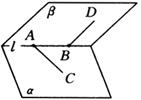
例11 已知平面![]() 与平面
与平面![]() 相交于直线
相交于直线![]() ,
,![]() ,
,![]() 为直线
为直线![]() 上的两点.在
上的两点.在![]() 内作直线
内作直线![]() ,在
,在![]() 内作直线
内作直线![]() .求证
.求证![]() 和
和![]() 是异面直线.
是异面直线.
已知:平面![]()
![]() 平面
平面![]() =
=![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,如图.
,如图.
求证:![]() 、
、![]() 是异面直线.
是异面直线.
证明:假设![]() ,
,![]() 不是异面直线,则它们必共面.
不是异面直线,则它们必共面.
∴![]() 、
、![]() 、
、![]() 、
、![]() 在同一平面内.
在同一平面内.
即![]() 、
、![]() 、
、![]() 所确定的平面
所确定的平面![]() 与
与![]() 、
、![]() 、
、![]() 确定的平面
确定的平面![]() 重合
重合
这与平面![]()
![]() 平面
平面![]() =
=![]() 矛盾
矛盾
∴![]() 、
、![]() 是异面直线.
是异面直线.
说明:证明两条直线为异面直线,用反证法往往比较简单.
典型例题十二
例12 已知空间四边形![]() ,求证它的对角线
,求证它的对角线![]() 和
和![]() 是异面直线.
是异面直线.
证法一:(反证法)如图
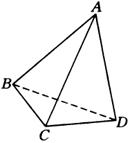
假设![]() 和
和![]() 不是异面直线,则
不是异面直线,则![]() 和
和![]() 在同一平面内.
在同一平面内.
∴![]() 、
、![]() 、
、![]() 、
、![]() 在同一平面内,即四边形
在同一平面内,即四边形![]() 是平面四边形,
是平面四边形,
这与已知条件矛盾,所以假设不成立.
因此![]() 和
和![]() 是异面直线.
是异面直线.
证法二:(定理法)
过![]() 和
和![]() 作一平面
作一平面![]() ,则对角线
,则对角线![]() 在平面
在平面![]() 内.
内.
对角线![]() 与平面
与平面![]() 交于
交于![]() 外的一点
外的一点![]() ,即点
,即点![]() 不在直线
不在直线![]() 上,
上,
且![]() 点在平面
点在平面![]() 外.
外.
∴根据异面直线判定定理知:![]() 和
和![]() 是异面直线.
是异面直线.
说明:判定两条直线是异面直线的证明问题常用这两种方法,即(1)反证法,(2)用判定定理.
典型例题十三
例13 已知空间四边形![]() ,
,![]() ,
,![]() 是
是![]() 的
的![]() 边上的高,
边上的高,![]() 是
是![]() 的
的![]() 边上的中线,求证:
边上的中线,求证:![]() 和
和![]() 是异面直线.
是异面直线.
证法一:(定理法)如图
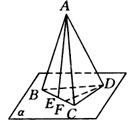
由题设条件可知点![]() 、
、![]() 不重合,设
不重合,设![]() 所在平面
所在平面![]() .
.
∴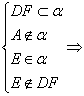
![]() 和
和![]() 是异面直线.
是异面直线.
证法二:(反证法)
若![]() 和
和![]() 不是异面直线,则
不是异面直线,则![]() 和
和![]() 共面,设过
共面,设过![]() 、
、![]() 的平面为
的平面为![]() .
.
(1)若![]() 、
、![]() 重合,则
重合,则![]() 是
是![]() 的中点,这与题设
的中点,这与题设![]() 相矛盾.
相矛盾.
(2)若![]() 、
、![]() 不重合,
不重合,
∵![]() ,
,![]() ,
,![]() ,∴
,∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() 、
、![]() 、
、![]() 、
、![]() 四点共面,这与题设
四点共面,这与题设![]() 是空间四边形相矛盾.
是空间四边形相矛盾.
综上,假设不成立.
故![]() 和
和![]() 是异面直线.
是异面直线.
说明:反证法不仅应用于有关数学问题的证明,在其他方面也有广泛的应用.
首先看一个有趣的实际问题:
“三十六口缸,九条船来装,只准装单,不准装双,你说怎么装?”
对于这个问题,同学们可试验做一做.
也许你在试验几次后却无法成功时,觉得这种装法的可能性是不存在的.那么你怎样才能清楚地从理论上解释这种装法是不可能呢?
用反证法可以轻易地解决这个问题.假设这种装法是可行的,每条船装缸数为单数,则9个单数之和仍为单数,与36这个双数矛盾.只须两句话就解决了这个问题.
典型例题十四
例14 已知![]() 、
、![]() 分别是正方体
分别是正方体![]() 的棱
的棱![]() 、
、![]() 的中点.
的中点.
求证:![]() .
.
分析:欲证两个角相等,可通过等角定理或其推论来实现.
证明:如图,连结![]()
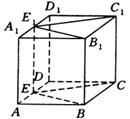
∵![]() ,
,![]() 分别为
分别为![]() ,
,![]() 中点,
中点,
∴![]()
![]()
![]() ,
,
∴![]() 为平行四边形.
为平行四边形.
∴![]()
![]()
![]() .
.
又∵![]()
![]()
![]() ,∴
,∴![]()
![]()
![]() ,
,
∴四边形![]() 是平行四边形.
是平行四边形.
∴![]() .同理
.同理![]() .又
.又![]() 与
与![]() 方向相同.
方向相同.
∴![]() .
.
说明:有关证明角相等问题,一般采用下面三种途径:(1)利用等角定理及其推论;(2)利用证三角形相似;(3)利用证三角形全等.
本例是通过第一种途径来实现.请同学们再利用第三种途径给予证明.
典型例题十五
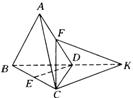
例15 由四个全等的等边三角形的封面几何体称为正四面体,如图,正四面体![]() 中,
中,![]() 、
、![]() 分别是棱
分别是棱![]() 、
、![]() 的中点,
的中点,![]() 与
与![]() 是一对异面直线,在图形中适当的选取一点作出异面直线
是一对异面直线,在图形中适当的选取一点作出异面直线![]() 、
、![]() 的平行线,找出异面直线
的平行线,找出异面直线![]() 与
与![]() 成的角.
成的角.
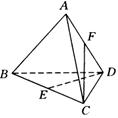
分析1:选取平面![]() ,该平面有以下两个特点,(1)该平面包含直线
,该平面有以下两个特点,(1)该平面包含直线![]() ,(2)该平面与
,(2)该平面与![]() 相交于点
相交于点![]() ,伸展平面
,伸展平面![]() ,在该平面中,过点
,在该平面中,过点![]() 作
作![]() 交
交![]() 的延长线于
的延长线于![]() ,连结
,连结![]() .可以看出:
.可以看出:![]() 与
与![]() 所成的角,即为异面直线
所成的角,即为异面直线![]() 与
与![]() 所成的角.如图.
所成的角.如图.
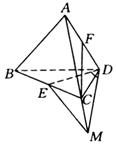
分析2:选取平面![]() ,该平面有以下两个特点:(1)该平面包含直线
,该平面有以下两个特点:(1)该平面包含直线![]() ,(2)该平面与
,(2)该平面与![]() 相交于点
相交于点![]() .在平面
.在平面![]() 中,过点
中,过点![]() 作
作![]() 的平行线交
的平行线交![]() 于点
于点![]() ,连结
,连结![]() ,可以看出:
,可以看出:![]() 与
与![]() 所成的角,即为异面直线
所成的角,即为异面直线![]() 与
与![]() 所成的角.如图.
所成的角.如图.
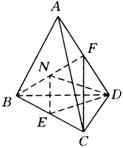
分析3:选取平面![]() ,该平面有如下两个特点:(1)该平面包含直线
,该平面有如下两个特点:(1)该平面包含直线![]() ,(2)该平面与
,(2)该平面与![]() 相交于点
相交于点![]() .在平面
.在平面![]() 中,过点
中,过点![]() 作
作![]() ,与
,与![]() 相交于点
相交于点![]() ,连结
,连结![]() ,可以看出:
,可以看出:![]() 与
与![]() 所成的角,即为异面直线
所成的角,即为异面直线![]() 与
与![]() 所成的角.
所成的角.
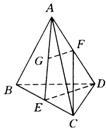
分析4:选取平面![]() ,该平面有如下特点:(1)该平面包含直线
,该平面有如下特点:(1)该平面包含直线![]() ,(2)该平面与
,(2)该平面与![]() 相交于点
相交于点![]() ,伸展平面
,伸展平面![]() ,在该平面内过点
,在该平面内过点![]() 作
作![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,且
,且![]() ,连结
,连结![]() ,则
,则![]() 与
与![]() 所成的角,即为异面直线
所成的角,即为异面直线![]() 与
与![]() 所成的角.如图.
所成的角.如图.
说明:(1)两条异面直线所成的角是非常重要的知识点,是每年高考的必考内容,要求牢固掌握两条异面直线所成的角的定义和两条异面直线互相垂直的概念,两条异面直线所成的角是刻划两条异面直线相对位置的一个量,是通过转化为相交直线成角来解决的,这里我们要注意:两条异面直线所成的角![]() 的范围是
的范围是![]() ,当
,当![]() 时,这两条异面直线互相垂直.求两条异面直线所成角的关键是作出这两条异面直线所成的角,作两条异面直线所成的角的方法是:将其中一条平移到某个位置使其与另一条相交或是将两条异面直线同时平移到某个位置使它们相交,然后在同一平面内求相交直线所成的角.值得注意的是:平移后相交所得的角必须容易算出,因此平移时要求选择恰当位置.一般提倡像思考2,那样作角,因为此角在几何体内部,易求.
时,这两条异面直线互相垂直.求两条异面直线所成角的关键是作出这两条异面直线所成的角,作两条异面直线所成的角的方法是:将其中一条平移到某个位置使其与另一条相交或是将两条异面直线同时平移到某个位置使它们相交,然后在同一平面内求相交直线所成的角.值得注意的是:平移后相交所得的角必须容易算出,因此平移时要求选择恰当位置.一般提倡像思考2,那样作角,因为此角在几何体内部,易求.
(2)本例题多方位、多角度思考问题,思路开阔、运用知识灵活,对我们解决异面直线所成角问题大有裨益,要认真理解.
典型例题十六
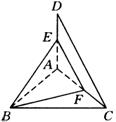
例16 如图,等腰直角三角形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,若
,若![]() ,且
,且![]() 为
为![]() 的中点.
的中点.
求异面直线![]() 与
与![]() 所成角的余弦值.
所成角的余弦值.
分析:根据异面直线所成角的定义,我们可以选择适当的点,分别引![]() 与
与![]() 的平行线,换句话说,平移
的平行线,换句话说,平移![]() (或
(或![]() ).设想平移
).设想平移![]() ,沿着
,沿着![]() 的方向,使
的方向,使![]() 移向
移向![]() ,则
,则![]() 移向
移向![]() 的中点
的中点![]() ,这样
,这样![]() 与
与![]() 所成的角即为
所成的角即为![]() 或其补角,解
或其补角,解![]() 即可获解.
即可获解.
解:取![]() 的中点
的中点![]() ,连结
,连结![]() ,在
,在![]() 中,
中,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,
的中点,
∴![]() ,
,
∴![]() 即为所求的异面直线
即为所求的异面直线![]() 与
与![]() 所成的角或其补角.
所成的角或其补角.
在![]() 中,
中,![]() ,
,![]() ,∴
,∴![]() .
.
在![]() 中,
中,![]() ,
,![]() ,∴
,∴![]() .
.
在![]() 中,
中,![]() ,
,![]() ,∴
,∴![]() .
.
在等腰三角形![]() 中,
中,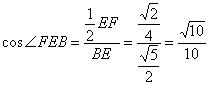 ,
,
∴异面直线![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() .
.
说明:求角或求角的三角函数值的一般步骤是:①找(或作出)角,适合题意,②求角或求角的三角函数值,往往是化归成一个三角形的内角,通过解三角形求得.
典型例题十七
例17 在正四面体![]() 中,已知
中,已知![]() 是棱
是棱![]() 的中点,求异面直线
的中点,求异面直线![]() 和
和![]() 所成角的余弦值.
所成角的余弦值.
分析:可在平面![]() 内过
内过![]() 作
作![]() 平行线,可在
平行线,可在![]() 中求得所成角的余弦值.
中求得所成角的余弦值.
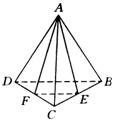
解:如图,取![]() 的中点
的中点![]() ,连结
,连结![]() ,
,![]() ,
,
∵![]() 为
为![]() 的中点,
的中点,
∴![]() 为
为![]() 的中位线,∴
的中位线,∴![]() ,
,
∴![]() 与
与![]() 所成的锐角或直角就是异面直线
所成的锐角或直角就是异面直线![]() 和
和![]() 所成的角.
所成的角.
设正四面体的棱长为![]() ,由正三角形的性质知,
,由正三角形的性质知,
![]() ,
,![]() .在
.在![]() 中,
中,
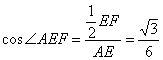 ,即异面直线
,即异面直线![]() 和
和![]() 所成角的余弦值为
所成角的余弦值为![]() .
.
说明:本题是利用三角形中位线达到平移的目的.这种作异面直线所成角的方法称为中位线平移法.
典型例题十八
例18 在正方体![]() 中,求正方体对角线
中,求正方体对角线![]() 和面对角线
和面对角线![]() 所成角的大小.
所成角的大小.
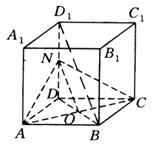
解:如图.
取![]() 上中点
上中点![]() ,则有:
,则有:![]() ,
,
连结![]() .令
.令![]() ,则
,则![]() ,
,
连结![]() ,
,![]() ,
,![]()
∵![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,
∴![]()
![]()
![]() ,
,
∴![]() (或
(或![]() )是异面直线
)是异面直线![]() 和
和![]() 所成的角.
所成的角.
在![]() 及
及![]() 中,
中,
∵![]() ,
,![]() ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,
∴![]() 为等腰三角形.
为等腰三角形.
又![]() 为
为![]() 中点,
中点,
∴![]() ,
,
∴异面直线![]() 和
和![]() 所成角为
所成角为![]() .
.
说明:(1)由于异面直线所成角最大为直角,所以,在把异面直线平移得到的两个夹角中,必须选取其中较小的角为异面直线的所成角.
(2)实际上,正方体的体对角线与任意一条面对角线所成角均为直角.
典型例题十九
例19 在正方体![]() 中,
中,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,求
的中点,求![]() 、
、![]() 所成角的余弦值.
所成角的余弦值.
分析1:可平移![]() 至
至![]() ,可得到角
,可得到角![]() ,再解三角形即可.但要注意到
,再解三角形即可.但要注意到![]() 为钝角.
为钝角.
解法1:如图,
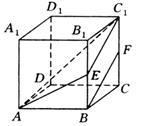
连结![]() ,则
,则![]() ,
,
由![]() 与
与![]() 所成的锐角或直角,就是
所成的锐角或直角,就是![]() 与
与![]() 所成的角,
所成的角,
连![]() ,令正方体的棱长为
,令正方体的棱长为![]() ,
,
有![]() ,
,![]()
在![]() 中,
中,![]() ,
,
∴![]() 的补角为异面直线
的补角为异面直线![]() 与
与![]() 所成角.
所成角.
∴![]() 、
、![]() 所成角的余弦值是
所成角的余弦值是![]() .
.
分析2:连结![]() 、
、![]() ,可得
,可得![]() 即为异面直线
即为异面直线![]() 和
和![]() 所成的角.进而求其余弦值.
所成的角.进而求其余弦值.
解法2:连结![]() 、
、![]() ,可证得
,可证得![]() .(∵
.(∵![]()
![]()
![]() )
)
![]() (或其补角)即为异面直线
(或其补角)即为异面直线![]() 、
、![]() 所成的角.
所成的角.
![]() ,
,![]() .
.
由余弦定理,有
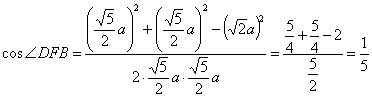 ,
,
∴![]() 、
、![]() 所成角的余弦值是
所成角的余弦值是![]() .
.
说明:异面直线所成角的范围是![]() ,当求得某角的余弦值为负值时,则此角的补角是异面直线所成角.
,当求得某角的余弦值为负值时,则此角的补角是异面直线所成角.
典型例题二十
例20 在空间四边形![]() 中:
中:![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点.求证:线段
的中点.求证:线段![]() 是异面直线
是异面直线![]() ,
,![]() 的公垂线.
的公垂线.
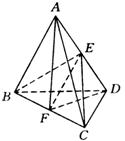
证明:如图.
连结![]() 、
、![]() 、
、![]() 、
、![]() .
.
在![]() 和
和![]() 中,
中,
![]() ,
,![]() ,
,![]() 公用
公用
∴![]() ≌
≌![]() .
.
又![]() 是
是![]() 中点,
中点,
∴![]() .
.
在![]() 中,
中,![]() 是
是![]() 的中点,
的中点,
∴![]() .
.
同理![]() ,
,
∴![]() 是异面直线
是异面直线![]() 、
、![]() 的公垂线.
的公垂线.
说明:证明某一条直线是两条异面直线的公垂线,须证明以下两点:(1)与两条异面直线都垂直;(2)与两条异面直线都相交.
典型例题二十一
例21 如图,空间四边形![]() 中,四边
中,四边![]() 、
、![]() 、
、![]() 、
、![]() 和对角线
和对角线![]() 、
、![]() 都等于
都等于![]() ,
,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点.
的中点.
(1)求证:![]() 是异面直线
是异面直线![]() 、
、![]() 的公垂线.
的公垂线.
(2)求异面直线![]() 和
和![]() 的距离.
的距离.
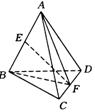
分析:要证明![]() 是异面直线
是异面直线![]() 与
与![]() 的公垂线,必须说明两个方面的问题,一个方面
的公垂线,必须说明两个方面的问题,一个方面![]() 与
与![]() 、
、![]() 都相交,另一个方面
都相交,另一个方面![]() 、
、![]() 与
与![]() 都垂直.
都垂直.
(1)证明:连结![]() 、
、![]() ,由已知
,由已知![]() 和
和![]() 均为正三角形,
均为正三角形,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,∴
的中点,∴![]() ,
,![]() .
.
同理![]() ,又
,又![]() 与
与![]() 、
、![]() 都相交,
都相交,
∴![]() 为异面直线
为异面直线![]() 、
、![]() 的公垂线.
的公垂线.
(2)解:∵空间四边形各边及对角线![]() 、
、![]() 的长均为
的长均为![]() ,
,
∴![]() ,而
,而![]() ,
,
∴在![]() 中,
中,![]() .
.
∴异面直线![]() 和
和![]() 之间的距离为
之间的距离为![]() .
.
说明:(1)求线段的长度一般地要把该线段放到一个三角形中去求解,尤其是放到特殊三角形中去求解,如直角三角形、等腰三角形等.
(2)满足条件的该空间四边形其实质是空间正四面体,该问题实质上是求正四面体对棱之间的距离.
典型例题二十二
例22 已知![]() 、
、![]() 是异面直线,直线
是异面直线,直线![]()
![]() 直线
直线![]() ,那么
,那么![]() 与
与![]() ( ).
( ).
A.一定是异面直线 B.一定是相交直线
C.不可能是平行直线 D.不可能是相交直线
解:由已知![]() 、
、![]() 是异面直线,直线
是异面直线,直线![]()
![]() 直线
直线![]() ,所以直线
,所以直线![]()
![]() 直线
直线![]() ,否则若
,否则若![]() ,则有
,则有![]() 与已知矛盾.所以
与已知矛盾.所以![]()
![]()
![]() .
.
∴应选C.
说明:本题考察两直线位置关系和公理4的应用及异面直线定义.
典型例题二十三
例23 两条异面直线指的是( ).
A.在空间内不相交的两条直线
B.分别位于两个不同平面内的两条直线
C.某平面内的一条直线和这个平面外的一条直线
D.不在同一平面内的两条直线
解:对于A,在空间内不相交的两条直线也可能是平行,应排除A.
对于B,分别位于两个不同平面内的两条直线可能是异面直线,
也可能是相交直线或平行直线,应排除B.
对于C,某平面内的一条直线和这个平面外的一条直线可能是异面直线,
也可能是平行直线,应排除C.
∴应选D.
说明:本题主要考查对异面直线定义的掌握,特别是对“不同在任何一个平面内的两条直线”含义的理解.
典型例题二十四
例24 如图,在棱长为1的正方体![]() 中,
中,![]() 、
、![]() 分别为
分别为![]() 和
和![]() 的中点,那么直线
的中点,那么直线![]() 与
与![]() 所成的角的余弦值是( ).
所成的角的余弦值是( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
解:在平面![]() 中,过
中,过![]() 点作
点作![]() ,交
,交![]() 于
于![]() ,连结
,连结![]() ,如图,
,如图,
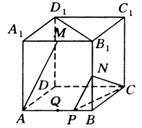
![]() (或其补角)就是
(或其补角)就是![]() 与
与![]() 所成的角.
所成的角.
设![]() 的中点为
的中点为![]() ,则
,则![]() 是
是![]() 中点.
中点.
可求得![]() ,
,![]() ,
,![]() .
.
在![]() 中,由余弦定理得
中,由余弦定理得
![]() .
.
∴应选D.
说明:作出平行线![]() ,进而在
,进而在![]() 中利用余弦定理求出直线
中利用余弦定理求出直线![]() 与
与![]() 所成角的余弦值.
所成角的余弦值.
典型例题二十五
例25 如图,![]() 是正方体,
是正方体,![]() ,则
,则![]() 与
与![]() 所成的角的余弦值是( ).
所成的角的余弦值是( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
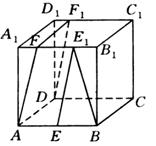
解:过![]() 点在平面
点在平面![]() 内作
内作![]() ,再过
,再过![]() 在平面
在平面![]() 内作
内作![]() ,
,
则![]() (或其补角)即是
(或其补角)即是![]() 与
与![]() 所成的角.
所成的角.
由已知![]() ,
,
![]() 是正方体,所以可求得
是正方体,所以可求得![]() (
(![]() 为正方体的棱长),
为正方体的棱长),
又![]() ,而
,而![]() ,
,
∴![]() ,显然
,显然![]() .
.
在![]() 中,由余弦定理,得
中,由余弦定理,得
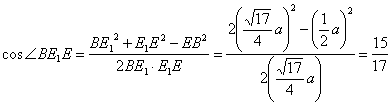 .
.
∴应选A.
说明:(1)解答本题的关键是作平行线![]() 、
、![]() .进而在
.进而在![]() 中解出
中解出![]() 的余弦值;(2)考查历届高考试题,求异面直线所成角的题常以正方体和正四面体为载体,在正方体和正四面体中命题.
的余弦值;(2)考查历届高考试题,求异面直线所成角的题常以正方体和正四面体为载体,在正方体和正四面体中命题.
典型例题二十六
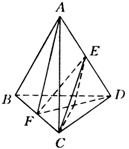
例26 在棱长都相等的四面体![]() 中,
中,![]() 、
、![]() 分别是棱
分别是棱![]() 、
、![]() 的中点,连结
的中点,连结![]() 、
、![]() ,如图所示,求异面直线
,如图所示,求异面直线![]() 、
、![]() 所成角的余弦值.
所成角的余弦值.
解:连结![]() ,取
,取![]() 的中点
的中点![]() ,连结
,连结![]() ,
,![]() ,
,
又![]() 是
是![]() 的中点,故
的中点,故![]() ,所以
,所以![]() 是异面直线
是异面直线![]() 、
、![]() 所成角.
所成角.
∵![]() 是正三角形
是正三角形![]() 的高,
的高,
∴![]() ,∴
,∴![]() .
.
在![]() 中,
中,![]() ,
,![]() ,则
,则
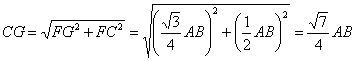 .
.
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
用余弦定理可得![]() .
.
∴异面直线![]() 、
、![]() 所成角的余弦值是
所成角的余弦值是![]() .
.
说明:求两条异面直线所成角或求所成角的函数值,关键是作出异面直线所成的角.
作两条异面直线所成角的方法一般是:将其中一条平移到某个位置使其也另一条相交也或者将两条异面直线同时平移到某个位置使它们相交,使得这个角在某一个平面的三角形内,进而求出.但要注意:平移后相交所得的角必须容易算出,因此平移时应选择恰当的位置.