高二数学必修3与选修2-1试卷
一、选择题(本大题有6小题,每小题5分,共30分,在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.用二分法求方程![]() 的近似根的算法中,要用到的算法结构为(
)
的近似根的算法中,要用到的算法结构为(
)
A 顺序结构 B 条件结构 C 循环结构 D 以上都用
2.已知命题P:“若x+y=0,则x,y互为相反数”命题P的否命题为Q,命题Q的逆命题为R,则R是P的逆命题的( )
A 逆命题 B 否命题 C 逆否命题 D 原命题
3.设有一个正方形网格,每个小正方形的边长为4,用直径等于1的硬币投掷到此网格上,硬币下落后与网格线没有公共点的概率为( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
4.根据如图伪代码,可知输出的结果S为( ) 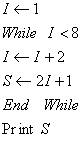
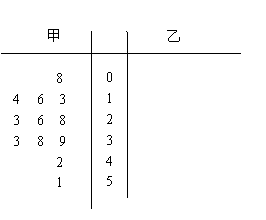
A.17 B
5.已知某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图如图所示,则甲、乙两人得分的中位数之和是( )
A 62 B
|

6.点P到点A(![]() ,B(a,2)及到直线
,B(a,2)及到直线![]() 的距离都相等,若这样的点恰好只有一个,则a的值为( )
的距离都相等,若这样的点恰好只有一个,则a的值为( )
A.![]() B
B ![]() C
C ![]() D
D ![]()
二、填空题(本大题有10小题,每小题5分,共50分.)
7.将一颗骰子掷600次,估计掷出的点数不大于2的次数大约是 ▲ .
8.某校高级职称教师26人,中级职称教师104人,其他教师若干人.为了了解该校教师的工资收入情况,若按分层抽样从该校的所有教师中抽取56人进行调查,已知从其它教师中共抽取了16人,则该校共有教师人. ▲ .
9.中心在原点,对称轴为坐标轴,离心率为![]() ,长轴长为8的椭圆方程为 ▲ .
,长轴长为8的椭圆方程为 ▲ .
10.若抛物线![]() 的焦点与双曲线
的焦点与双曲线![]() 的右焦点重合,则实数
的右焦点重合,则实数![]() = ▲ .
= ▲ .
11.一组数据中的每个数据都减去80得一组新数据,若这组新数据的平均数是1.2,
方差为4.4则原数据的平均数和方差分别为 ▲ .
12.命题“任意满足![]() 的实数x,有x>
的实数x,有x>
13.若10把钥匙中有两把能打开某锁,则从中任取2把能将该锁打开的概率为 ▲ .
14.已知抛物线![]() 上的任意一点P,记点P到
上的任意一点P,记点P到![]() 轴的距离为
轴的距离为![]() ,对于给定点
,对于给定点![]() ,则
,则![]() 的最小值为 ▲ .
的最小值为 ▲ .
15.双曲线![]() 左支上一点
左支上一点![]() 到其渐近线
到其渐近线![]() 的距离是
的距离是![]() ,则
,则![]() 的值为
的值为
▲ .
16.为激发学生学习兴趣,老师上课时在黑板上写出三个集合:![]() ,
,![]() ,
,![]() ;然后请甲、乙、丙三位同学到讲台上,并将“[]”中的数告诉了他们,要求他们各用一句话来描述,以便同学们能确定该数,以下是甲、乙、丙三位同学的描述,甲:此数为小于6的正整数;乙:A是B成立的充分不必要条件;丙:A是C成立的必要不充分条件.若三位同学说的都对,则“[]”中的数为 ▲ .
;然后请甲、乙、丙三位同学到讲台上,并将“[]”中的数告诉了他们,要求他们各用一句话来描述,以便同学们能确定该数,以下是甲、乙、丙三位同学的描述,甲:此数为小于6的正整数;乙:A是B成立的充分不必要条件;丙:A是C成立的必要不充分条件.若三位同学说的都对,则“[]”中的数为 ▲ .
新课标高二试卷(2)(必修3与选修2-1)
一.选择题答案:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 |
| 答案 |
二.填空题答案:
7.__________________ ; 8._______________________;
9.__________________ ; 10.______________________;
11._________________ ; 12.______________________;
13._________________ ; 14.______________________;
14._________________ ; 16.______________________.
三.解答题(本大题有6小题,共80分,解答应写出文字说明、证明过程或演算步骤.)
17.(本小题满分12分)将两颗正方体型骰子投掷一次,求:
(1)向上的点数之和是8的概率;
(2)向上的点数之和不小于8的概率.
18.(本小题满分12分)已知![]() 且
且![]() ,设
,设![]() :指数函数
:指数函数![]() 在
在![]() 上为减函数,
上为减函数,![]() :不等式
:不等式![]() 的解集为
的解集为![]() .若
.若![]() 和
和![]() 有且仅有一个正确,求
有且仅有一个正确,求![]() 的取值范围.
的取值范围.
19.(本小题满分12分)某班40个学生平均分成两组,两组学生某次考试的成绩情况如下表所示:
| 组别 | 平均数 | 标准差 |
| 第一组 | 90 | 4 |
| 第二组 | 80 | 6 |
求这次考试全班的平均成绩和标准差.( 注:平均数![]() ,
,
标准差![]() )
)
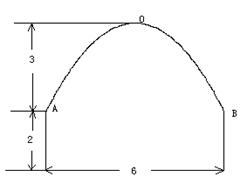
20.(本小题满分14分)一条隧道的横断面由抛物线弧及一个矩形的三边围成,尺寸如图所示(单位:![]() ),一辆卡车空车时能通过此隧道,现载一集装箱,箱宽3
),一辆卡车空车时能通过此隧道,现载一集装箱,箱宽3![]() ,车与箱共高
,车与箱共高![]() ,此车是否能通过隧道?并说明理由.
,此车是否能通过隧道?并说明理由.
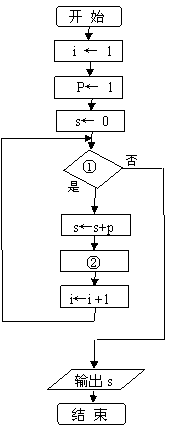
 21.(本小题满分14分)给出30个数:1,2,4,7…,其规律是:第一个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,依此类推,要计算这30个数的和,现已给出了该问题算法的流程图(如图所示):
21.(本小题满分14分)给出30个数:1,2,4,7…,其规律是:第一个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,依此类推,要计算这30个数的和,现已给出了该问题算法的流程图(如图所示):
(1)图中①处和②处应填上什么语句,使之能完成该题的算法功能;
(2)根据流程图写出伪代码.
22.(本小题满分16分)如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .
.![]() 于
于![]() 点,
点,![]() ,曲线
,曲线![]() 过点
过点![]() ,动点
,动点![]() 在
在![]() 上运动,且保持
上运动,且保持![]() 的值不变
的值不变
 (1)建立适当的坐标系,求曲线
(1)建立适当的坐标系,求曲线![]() 的方程;
的方程;
(2)过![]() 点的直线
点的直线![]() 与曲线
与曲线![]() 相交于不同的两点
相交于不同的两点![]() 、
、![]() ,且
,且![]() 在
在![]() 、
、![]() 之间,设
之间,设![]() ,试确定实数
,试确定实数![]() 的取值范围.
的取值范围.
参考答案
1.D 2.B 3.C 4.B 5.B 6.D![]()
7.200次 8.182 9.![]() 或
或![]() 10.4
10.4
11.81.2\4.4 12.存在满足![]() 的实数x,使得
的实数x,使得![]() 13.
13.![]()
14.![]() 15.
15.![]() 16.1
16.1
17.解:将两骰子投掷一次,共有36种情况,向上的点数之和的不同值共11种.
(1)设事件A={两骰子向上的点数和为8};
事件A![]() ={两骰子向上的点数分别为4和4};
={两骰子向上的点数分别为4和4};
事件A![]() ={两骰子向上的点数分别为3和5};
={两骰子向上的点数分别为3和5};
事件A![]() ={两骰子向上的点数分别为2和6},则A
={两骰子向上的点数分别为2和6},则A![]() 与A
与A![]() 、A
、A![]() 互为互斥事件,且A= A
互为互斥事件,且A= A![]() + A
+ A![]() + A
+ A![]()
故![]()
(2)设事件S={两骰子向上的点数之和不小于8};
事件A={两骰子向上的点数和为8};
事件B={两骰子向上的点数和为9};
事件C={两骰子向上的点数和为10};
事件D={两骰子向上的点数和为11};
事件E={两骰子向上的点数和为12}.则A,B,C,D,E互为互斥事件,且S=A+B+C+D+E.P(A)=![]() ,P(B)=
,P(B)=![]() ,P(C)=
,P(C)=![]() ,P(D)=
,P(D)=![]() ,P(E)=
,P(E)=![]() ,
,
故P(S)=P(A)+P(B)+P(C)+P(D)+P(E)=![]() +
+![]() +
+![]() +
+![]() +
+![]() =
=![]()
答:(1)向上的点数之和是8的概率为![]() ;(2)向上的点数之和不小于8的概率为
;(2)向上的点数之和不小于8的概率为![]() .
.
18.解:当![]() 正确时,
正确时,
![]() 函数
函数![]() 在
在![]() 上为减函数
上为减函数 ![]() ,
,
∴当![]() 为正确时,
为正确时,![]() ;
;
当![]() 正确时,
正确时,
∵不等式![]() 的解集为
的解集为![]() ,
,
∴当![]()
![]() 时,
时,![]() 恒成立.
恒成立.
∴![]() ,∴
,∴![]()
∴当![]() 为正确时,
为正确时,![]() .
.
由题设,若![]() 和
和![]() 有且只有一个正确,则
有且只有一个正确,则
(1)![]() 正确
正确![]() 不正确,∴
不正确,∴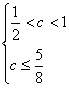 ∴
∴![]()
(2)![]() 正确
正确![]() 不正确∴
不正确∴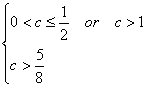 ∴
∴![]()
∴综上所述,若![]() 和
和![]() 有且仅有一个正确,
有且仅有一个正确,![]() 的取值范围是
的取值范围是![]()
19.解:设第一组同学的分数为![]() ,平均分为
,平均分为![]() ;第二组同学的分数为
;第二组同学的分数为![]() ,平均分为
,平均分为![]() .
.
依题意得:![]() ,∴
,∴![]()
同理:![]() ,
,![]()
设全班同学的平均成绩为![]() ,则
,则![]()
![]()
又![]()
∴![]() ,同理
,同理![]()
设全班分数的标准差为![]()
![]()
![]() .
.
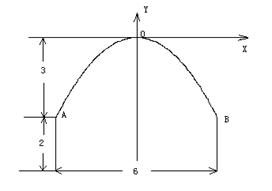 20.解:如图,建立坐标系,则A(-3,-3),B(3, -3).
20.解:如图,建立坐标系,则A(-3,-3),B(3, -3).
设抛物线方程为![]() ,
,
将B点坐标代入,得![]() ,
,
∴![]() .∴抛物线方程为
.∴抛物线方程为![]() .
.
∵车与箱共高![]() ∴集装箱上表面距抛物线型隧道拱顶
∴集装箱上表面距抛物线型隧道拱顶![]() .
.
设抛物线上点![]() 的坐标为
的坐标为![]() ,2则
,2则![]() ,
,
∴![]() ,∴
,∴![]() ,故此车不能通过隧道.
,故此车不能通过隧道.
21.解:(1)①![]() ②
②![]()
(2)伪代码: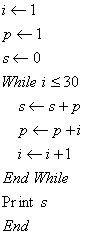
22.解:(1)建立平面直角坐标系,如图所示.
∵![]()
∴动点![]() 的轨迹是椭圆.
的轨迹是椭圆.
∵![]() ∴曲线
∴曲线![]() 的方程是
的方程是![]() .
.
(2)设直线![]() 的方程为
的方程为![]() ,代入曲线
,代入曲线![]() 方程,
方程,
得![]() ,
,
设![]() ,则
,则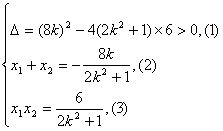
①![]() 与
与![]() 轴重合时,
轴重合时,![]() ;
;
②![]() 与
与![]() 轴不重合时,由(1)得
轴不重合时,由(1)得![]() .∵
.∵![]() ,
,
∵![]() 或
或![]() ∴
∴![]() ,
,
∴![]() ,
,
∵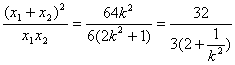 而
而![]() ,
,
∴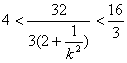 ∴
∴![]() ∴
∴![]() .
.
∴![]() 的取值范围是
的取值范围是![]() .
.