高二数学必修5期末考试卷2（，选修1-1）
一、填空题（14×5=70）
1．双曲线
的渐近线为__________________________________
2．命题：
的否定是
3.
在△ABC中，若
，则B等于_____________
4. x＞4是
＜
的___________________________条件
5. 椭圆
的长轴为
，点
是椭圆短轴的一个端点，且
，则离心率
等于_________________
6. 若不等式
的解集是
，则不等式
的解集
7. 椭圆
的一个焦点为（0，2），那么k=________________
8. 两等差数列{an}、{bn}的前n项和的比
，则
的值是________________
9. 在等差数列｛an｝中，已知公差d=
，且a1+a3+a5+…+a99=60，则a1+a2+a3+…+a99+a100=______________
10. 若双曲线 
的焦点是
过
的直线交左支于A、B，若AB=5，则△AF2B的周长是
11. 设
，则函数
的最小值是
12. 设等比数列｛an｝共有3n项，它的前2n项的和为100，后2n项之和为200，则该等比数列中间n项的和等于___________________
13. 已知非负实数a，b满足
最大值是
14. 方程 
表示的曲线为C，给出下列四个命题：
①若
，则曲线C为椭圆；
②若曲线C为双曲线，则
或
；
③若曲线C表示焦点在x轴上的椭圆，则
；
④曲线C不可能表示圆的方程. 其中正确命题的序号是 ．
二、解答题（12+12+16+16+16+18=90）
15. （本题满分12分）求右焦点坐标是
，且经过点
的椭圆的标准方程？
16. （本题满分12分）设双曲线的焦点在
轴上，两条渐近线为 
，求该双曲线离心率？
17. （本题满分16分）△
中，内角
的对边分别为
，已知成等比数列，
求（1）
的值； （2）设
，求
的值．
18. （本题满分16分） 已知命题p：方程
表示焦点在y轴上的椭圆，命题q：双曲线
的离心率
，若
只有一个为真，求实数
的取值范围．
19. （本题满分16分）已知f(x+1)=x2－4，等差数列｛an｝中，a1=f(x－1)，
a2=－
，a3=f(x)
（1）求x的值； （2）求通项an；（3）求a2+a5+a8+…+a26的值.
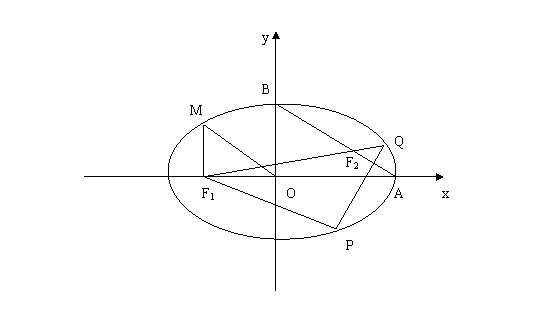
20. （本题满分18分）如图，从椭圆
（a>b>0）上一点M向x轴作垂线，恰好通过椭圆的左焦点F1，且它的长轴端点A及短轴端点B的连线AB//OM.
求（1）椭圆的离心率e；
（2）设Q是椭圆上任意一点，F2是右焦点，F1是左焦点，求
的取值范围；
（3）设Q是椭圆上一点，当
时，延长QF2与椭圆交于另一点P，若
的面积为
，求此时椭圆方程
高二数学试卷答案
1.
2.
3.
4.充分不必要 5.
6.
7.1
8.
9.145
10．18
11.6
12.
13.
14. 2 3
15．解：设椭圆的标准方程为
，
，
2分
∴
，即椭圆的方程为
，
6分
∵ 点（
）在椭圆上，∴ 
，
解得
或
（舍）， 10分
由此得
，即椭圆的标准方程为
.
12分
16.
17. 解：（1）由
，得
2分
由
及正弦定理得 
4分
于是
7分
（2）由
，得
，
8分
由
，可得
，即
．
10分
由余弦定理 
，得
，
．
14分
18．P:0<m<
4分
q:0<m<15 4分
p真q假，则空集 3分
p假q真，则
3分
故
2分
19. (1)0或3 4分
(2) an=n－
或 an= -n+ 9分
(3) 
或
14分
20. 解（1）由
轴可知
=-c
1分
将=-c代入椭圆方程得
2分
又
且OM//AB
3分
即b=c，
4分
（2）设
，
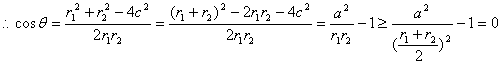7分
当且仅当
时，上式等号成立
故
9分
（3）
可设椭圆方程为
10分
11分
直线PQ的方程为
，代入椭圆方程得
13分
又点F1到PQ的距离d=
即c2=25，椭圆方程为
16分