高二数学必修5第三章同步测试

高二数学必修5第三章同步测试

班别__________　姓名__________　学号__________　成绩__________

一、选择题。（10×4分=40分）

1．若，且，则下列不等式一定成立的是　　　　　　　　　　　　　　　　　（　　）A．　　　 　　　　　　　　　　　　　　　　　　　 B．

C．　　　　 　　　　　　　　　　　　　　　 D．

2．若，则下列不等关系中，不能成立的是　　　　　　　　　　　　　　　 （　　）A．　　　　　　　　　　　　　　　　　　　　　 B． 　　　　C．　　D．　　　　　　　　　

3．若实数a、b满足a+b=2，是的最小值是　　　　 　　　　　　　　　　　 （　　）A．18　　  B．6 　　　　　　　　　　　　　　　　　　　　C．2　 　　　　　　　　　　D．2

4．如果不等式ax²+bx+c<0 (a≠0)的解集是φ,那么 　　　　　　　　　　　　(　　)

A．a<0，且b²-4ac>0 　　　　　　 B．a<0且b²-4ac≤0　

C．a>0且b²-4ac≤0 　　　　　 D．a>0且b²-4ac>0　

5．若角α，β满足－＜α＜，－＜β＜则2α＋β的取值范围是　　　　　　　　（ 　　）A．（－π，0）　　B．（－π，π）　　　　　　　　　　　　 C．（－，）　　 D．（－，）

6．有以下四个命题，其中真命题为  　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （  　 　）

A．原点与点（2,3）在直线２x＋y+3＝０异侧

B．点（2,3）与点（3,2）在直线x－y=0的同侧

C．原点与点（2,1）在直线y－3x＋2 =0的异侧

D．原点与点（2,1）在直线y－3x＋2 =0的同侧

7．不等式3x－2y－6>0表示的区域在直线3x－2y－6＝0 的　　　　　　　　　  　　　　　（　　　 ）

A．右上方　　 　 B．右下方　　　 C．左上方　 　　D．左下方

8．由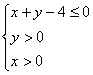所确定的平面区域内整点的个数是　　　 　　　　　　　　　 （　　　 ）

A．3个　　　　　  B．4个　　　　　  C．5个　　　　　  D．6个

9．已知x、y满足约束条件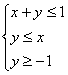，Z=2x+y的最大值是　　　　　　　　　  （　　 　）

A．－5　　　　　 B．　　　　　 C．3　　　　  D．5

10．下列选项正确的是

A．函数y=sin²a+ 4/sin²a的最小值是4　　B．函数y=sina+ 1/sina的最小值是2  C．+>+ 　　　　　　　　　 D．5⁸  > 3¹²

题号	1	2	3	4	5	6	7	8	9	10
答案

二、填空题。（4×4分=16分）

11、用三条直线x+2y=2，2x+y=2，x-y=3围成一个三角形，则三角形内部区域（不包括边界）

可用不等式表示为___________　　　　　 

12、已知：0＜x＜1，则函数y=x（3－2x）的最大值是___________

13、若x>5/4 ，则y=4x－1+的最小值是___________

14、某校伙食长期以面粉和大米为主食，而面食每100克含蛋白质6个单位，含淀粉4个单位，米食每100克含蛋白质3个单位，含淀粉7个单位，学校要求给学生配制盒饭，每盒饭至少有8个单位的蛋白质和10个单位的淀粉，设每盒盒饭需要面食x（百克），米

食y（百克）.用数学关系式表示上述要求的x,y: __________

三、解答题。（共44分）

15、比较下列各组中两个代数式的大小：

⑴x²+3与3x ；

⑵已知a,b为正数，且a≠b，比较a³ +b³与a²b+ab²

16、已知A={xㄧx²-3x-4<0 }，B={xㄧx²-4x+3>0 }，

　　求A∩B

17、不等式mx²－mx＋1>0，对任意实数x都成立，求m的取值范围。

18、某养鸡厂想筑一个面积为144平方米的长方形围栏。围栏一边靠墙，筑成这样的围栏最少要用多少米铁丝网？此时利用墙多长？

19、某汽车公司有两家装配厂，生产甲、乙两种不同型的汽车，若A厂每小时可完成1辆甲型车和2辆乙型车；B厂每小时可完成3辆甲型车和1辆乙型车。今欲制造40辆甲型车和乙型车，问这两家工厂各工作几小时，才能使所费的总工作时数最小

高二数学必修5第三章同步测试答案

一、选择题

题号	1	2	3	4	5	6	7	8	9	10
答案	D	C	B	A	A	C	B	D	C	C

二、填空题。

11、　　　　 12、　　　　　 13、6　　　　　　　 14、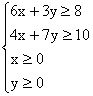

三、解答题。

15、解：（1）x²+3－3x　　　　　　　 （2）a³ +b³－（a²b+ab²）

　　　　  = x²－3x+－+3　　　　　 =（a³－a²b）+（b³－ab²）

　　　　  =（x－）²+＞0　　　　  = a²（a－b）+ b² (b－a)

　　 　 ∴  x²+3＞3x　　　　　　　　　 =( a²－b²)( a－b)

　　　　　　　　　　　　　　　　　　　  =( a－b)²( a+b)

　　　　　　　　　　　　　　　　　   ∵ a,b为正数，且a≠b

　　　　　　　　　　　　　　　　   ∴ ( a－b)²＞0, a+b＞0

　　　　　　　　　　　　　　　　　　 ∴ ( a－b)²( a+b) ＞0

　　　　　　　　　　　　　　　　　　 ∴ a³ +b³＞a²b+ab²

16、解：A={xㄧx²-3x-4<0 }={xㄧ-1< x <4 }

　　　　B={xㄧx²-4x+3>0 }={xㄧx >3或x <1}

　　　 A∩B={xㄧ-1< x <4 }∩{xㄧx >3或x <1}

　　　　　 ={xㄧ-1< x <1 或3< x <4}

17、解：当m=0时，1>0，不等式成立，∴　m=0

当m≠0时,则有

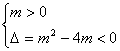
即 0<m<4

∴m的取值范围｛mㄧ0≤m<4 ｝

18、解：设长方形围栏的长为x米，宽为y米，要用铁丝网s米，则xy=144

　　　　S=x+2y≥2=2=24(米)

　　　　当x=2y,即x=12, y=6时,等号成立，S_min=24

　　　 ∴筑成这样的围栏最少要用24米铁丝网,此时利用墙12米。

19、解：设A厂工作x小时，B厂生产y小时，总工作时数为T小时，则它的目标函数为

T=x＋y 且x＋3y≥40 ，2x+y≥40 ，x≥0 ，y≥0

可行解区域如图，

由图知当直线l：y＝－x＋T过Q点时，纵截距T最小，

解方程组 得Q（16,8）　　　　

故A厂工作16小时，B厂工作8小时，可使所费的总工作时数最少。