数列综合测试

必修五 第二章数列综合测试

一、选择题：

1. 将自然数的前5个数：（1）排成1，2，3，4，5；（2）排成5，4，3，2，1；

（3）排成2，1，5，3，4；（4）排成4，1，5，3，2.

那么可以叫做数列的只有　　　　　　　　　　　　　　　　　　　　  　　　　　( 　 )

(A)（1）　(B)（1）和（2）　(C)（1），（2），（3）　(D)（1），（2），（3），（4）

2. 若数列{a_n}的通项公式是a_n=2(n＋1)＋3，则此数列　　　　　　　　　  　　　　 (　　)

(A)是公差为2的等差数列　　　　　　　　 (B)是公差为3的等差数列

(C) 是公差为5的等差数列　　　　　　　  (D)不是等差数列

3.等差数列{a_n}中，若a₂+a₄+a₉+a₁₁=32，则a₆+a₇=　　　　　　　　　　　 　　　　　(　　)

（A）9　　　　　  （B）12　　　　　　  （C）15　　　　　  （D）16

4.已知数列 满足： >0， ， ，则数列{ }是：　　　　  　（ 　　）

(A)递增数列　　　 ( B)递减数列　　　 (C)摆动数列　　　　(D)不确定

5.等差数列0， ，－7，…的第n+1项是：　　　　　　　　　　  　　　（　　）

(A) 　　　　　(B) 　　　 (C) 　　　(D)

6.在数列 中， ， 则 的值为：　　　　　  （　　 ）

（A）49　　　　　 （B）50　　　　　 （C）51　　　　　  (D)52

7．已知数列10 , …10 …,使数列前n项的乘积不超过10 最小正整数n是　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　

(A)9　　　　 (B)10　　　　　  (C)11　　　　  (D)12 　　　　　　　　　　 (　　)　

 8. 在首项为81，公差为－7的等差数列 中，最接近零的是第　　　　　　　　 (　　)

(A)11项　　　　　(B)12项　　　　　 (C)13项　　　　　 (D)14项

9. 已知等差数列{a_n}的公差d≠0,若a₅、a₉、a₁₅成等比数列,那么公比为　 　　　　　(　　)

(A) 　　　　　　　(B) 　　　　　 (C) 　　　　　　 (D)

10.现有200根相同的钢管，把它们堆放成正三角形垛，要使剩余的钢管尽可能少，那么剩余钢管的根数为　　　　　　　 　　　　　　　　　　　　　　　　　　　　　 (　　 )

　　(A)9　　　　　　  (B)10　　　　　　 (C)19　　　　　  (D)29

二、填空题：　

11．等差数列110，116，122，128，……，在400与600之间共有________项.

12. 设等比数列{a_n}的前n项和S_n，S₃ +S₆ =2S₉，则数列的公比为______________

13．已知数列1, ，则其前n项的和等于　　　　 

14．数列的第一项为1，并且对n∈N,n≥2都有：前n项之积为n²，则此数列的通项公式为

_______　　　　 

三．解答题：

15． 三个互不相等的数成等差数列，如果适当排列这三个数，也可成等比数列，已知这三个数的和等于6，求此三个数。

　

　

16.等差数列 的项数m是奇数, 且a₁ + a₃ + …+a_m = 44 , a₂ + a₄ +…+a_m－1 ＝33 , 求m的值.

　

17.  已知数列 中， ，当 时， ，

（1）证明数列 是一个等差数列； （2）求 .



 

_{18.等差数列{an}的前n项和为Sn,S4=－62,S6=－75设bn=an ，求数列{bn}的前n项和Tn.}

　

　

　

19. 数列 是等比数列， ＝8，设 （ ），如果数列 的前7项和 是它的前n项和组成的数列 的最大值，且 ，求 的公比q的取值范围．　

　

　

20.设{a_n}是正数组成的数列，其前n项和为S_n,并且对于所有的n N₊,a_n与2的等差中项等于S_n与2的等比中项.

1)　　 写出数列{a_n}的前3项.

2)　　 求数列{a_n}的通项公式(写出推证过程)

数列单元测试卷（答案）

DADBA　　 DCCCB

11．33　　 12. 　 13． 　　　14．a_n=

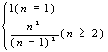
15． 解：设三个数分别为 a-d,a,a+d　 则 （a－d）＋a＋(a＋d)=3a＝6　 a=2

三个数分别为　2－d,2,2＋d　∵它们互不相等 ∴分以下两种情况：

当(2－d)²=2(2＋d)时，　 d=6　三个数分别为-4,2,8

当(2＋d)²=2(2－d)时，　 d=-6 三个数分别为8,2,-4

因此，三个数分别为-4,2,8　或8,2,-4

16. 解： 由已知可得

（1）－（2）得

（1）+（2）得

所以　　11m=77　　　即　　m=7

17. 解：１）当n=1时，S₁=a₁=1 当 n≥2时a_n=S_n-S_n-1= ( + )( - ) = 而 + ≠0 ∴ - =
　　∴数列 是一个等差数列。
　（2）由（1）得 = 　S_n=( )²当n=1时 a₁=S₁当n>1时
　　 a_n=S_n-S_n-1= 　　 ∴a_n=
 _{18.解：由S4=－62,S6=－75解得d=3　a1=－20　∴an=3n－23　设从第n+1项开始大于零 则 　　∴ ∴n=7即 a7<0,a8>0
　　　当1≤n≤7时 Tn=－Sn=
　　　当n≥8  时　 Tn=
　　 综上有Tn=}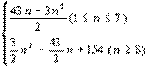
 19. 解：{ }为等比数列，设公比为q ,由
　　 　　　　 则 ，
　　　　　　∴{ }为首项是3，公差为 的等差数列；　　由 最大，且
　　　　　　∴ 且 　 ∴3+6 ≥0 且3+7 ≤0
　　　　　　∴ 　　 ∴ 　即
　20.解：1)由题意，当n=1时，有 ，S₁=a₁,

∴ 　a₁=2　　　当n=2时　有 　 S₂=a₁+a₂　a₂>0　

　得a₂=6　　　　　  同理　 a₃=10　 故该数列的前三项为2,6,10.

　　 2) 由题意， 　　　　 ∴S_n= ,S_n+1=

　　　 ∴a_n+1=S_n+1-S_n= 　 ∴(a_n+1+a_n)(a_n+1-a_n-4)=0

　　　 ∵a_n+1+a_n≠0，∴a_n+1-a_n=4  即数列{a_n}为等