典型例题一
例1 已知椭圆
的一个焦点为（0，2）求
的值．
分析：把椭圆的方程化为标准方程，由
，根据关系
可求出的值．
解：方程变形为
．
因为焦点在
轴上，所以
，解得
．
又，所以
，
适合．故．
典型例题二
例2 已知椭圆的中心在原点，且经过点
，
，求椭圆的标准方程．
分析：因椭圆的中心在原点，故其标准方程有两种情况．根据题设条件，运用待定系数法，求出参数
和
（或
和
）的值，即可求得椭圆的标准方程．
解：当焦点在
轴上时，设其方程为
．
由椭圆过点，知
．又，代入得
，
，故椭圆的方程为
．
当焦点在轴上时，设其方程为
．
由椭圆过点，知．又，联立解得
，
，故椭圆的方程为
．
典型例题三
例3 
的底边
，
和
两边上中线长之和为30，求此三角形重心
的轨迹和顶点
的轨迹．
分析：（1）由已知可得
，再利用椭圆定义求解．（2）由的轨迹方程、坐标的关系，利用代入法求的轨迹方程．
解：
（1）以
所在的直线为轴，中点为原点建立直角坐标系．设点坐标为
，由，知点的轨迹是以
、
为焦点的椭圆，且除去轴上两点．因
，
，有
，故其方程为
．
（2）设
，
，则
．
①
由题意有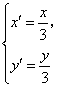
代入①，得的轨迹方程为
，其轨迹是椭圆（除去轴上两点）．
典型例题四
例4 已知
点在以坐标轴为对称轴的椭圆上，点到两焦点的距离分别为
和
，过点作焦点所在轴的垂线，它恰好过椭圆的一个焦点，求椭圆方程．
分析：讨论椭圆方程的类型，根据题设求出和（或和）的值．从而求得椭圆方程．
解：设两焦点为
、
，且
，
．
从椭圆定义知
．即
．
从
知
垂直焦点所在的对称轴，
所以在
中，
，
可求出
，
，从而
．
∴所求椭圆方程为
或
．
典型例题五
例5 已知椭圆方程，长轴端点为
，
，焦点为，，是椭圆上一点，
，
．求：
的面积（用、、
表示）．
分析：求面积要结合余弦定理及定义求角的两邻边，从而利用
求面积．
解：如图，设
，由椭圆的对称性，不妨设，
由椭圆的对称性，不妨设在第一象限．由余弦定理知：
·
．①
由椭圆定义知： 
②
则
得
．
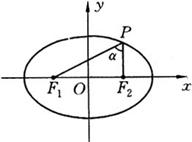
故
．
典型例题六
例6 已知椭圆
，
（1）求过点
且被平分的弦所在直线的方程；
（2）求斜率为2的平行弦的中点轨迹方程；
（3）过
引椭圆的割线，求截得的弦的中点的轨迹方程；
（4）椭圆上有两点、
，
为原点，且有直线
、
斜率满足
，求线段
中点
的轨迹方程．
分析：此题中四问都跟弦中点有关，因此可考虑设弦端坐标的方法．
解：设弦两端点分别为
，
，线段
的中点
，则
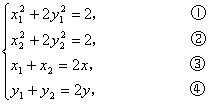
①－②得
．
由题意知
，则上式两端同除以
，有
，
将③④代入得
．
⑤
（1）将
，
代入⑤，得
，故所求直线方程为
．
⑥
将⑥代入椭圆方程
得
，
符合题意，
故即为所求．
（2）将
代入⑤得所求轨迹方程为：
．（椭圆内部分）
（3）将
代入⑤得所求轨迹方程为
．（椭圆内部分）
（4）由①＋②得
，
⑦
将③④平方并整理得
， ⑧
，
⑨
将⑧⑨代入⑦得
，
⑩
再将
代入⑩式得
，
即
．
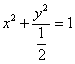此即为所求轨迹方程．当然，此题除了设弦端坐标的方法，还可用其它方法解决．
典型例题七
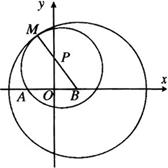例7 已知动圆过定点
，并且在定圆
的内部与其相内切，求动圆圆心的轨迹方程．
分析：关键是根据题意，列出点P满足的关系式．
解：如图所示，设动圆和定圆内切于点．动点到两定点，即定点和定圆圆心
距离之和恰好等于定圆半径，即
．
∴点的轨迹是以，为两焦点，半长轴为4，半短轴长为
的椭圆的方程：
．
说明：本题是先根据椭圆的定义，判定轨迹是椭圆，然后根据椭圆的标准方程，求轨迹的方程．这是求轨迹方程的一种重要思想方法．
典型例题八
例8 已知椭圆
及直线
．
（1）当为何值时，直线与椭圆有公共点？
（2）若直线被椭圆截得的弦长为
，求直线的方程．
分析：直线与椭圆有公共点，等价于它们的方程组成的方程组有解．因此，只须考虑方程组消元后所得的一元二次方程的根的判别式．已知弦长，由弦长公式就可求出．
解：（1）把直线方程代入椭圆方程得
，即
．
，
解得
．
（2）设直线与椭圆的两个交点的横坐标为
，
，由（1）得
，
．
根据弦长公式得
．
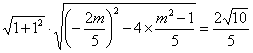解得
．
因此，所求直线的方程为
．
说明：处理有关直线与椭圆的位置关系问题及有关弦长问题，采用的方法与处理直线和圆的有所区别．这里解决直线与椭圆的交点问题，一般考虑判别式
；解决弦长问题，一般应用弦长公式．用弦长公式，若能合理运用韦达定理（即根与系数的关系），可大大简化运算过程．
典型例题九
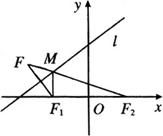例9 以椭圆
的焦点为焦点，过直线
上一点作椭圆，要使所作椭圆的长轴最短，点应在何处？并求出此时的椭圆方程．
分析：椭圆的焦点容易求出，按照椭圆的定义，本题实际上就是要在已知直线上找一点，使该点到直线同侧的两已知点（即两焦点）的距离之和最小，而这种类型的问题在初中就已经介绍过，只须利用对称的知识就可解决．
解：如图所示，椭圆的焦点为
，
．
点关于直线的对称点
的坐标为（－9，6），直线
的方程为
．解方程组
得交点的坐标为（－5，4）．此时
最小．
所求椭圆的长轴
，
∴
，又
，
∴
．
因此，所求椭圆的方程为
．
说明：解决本题的关键是利用椭圆的定义，将问题转化为在已知直线上求一点，使该点到直线同侧两已知点的距离之和最小．
典型例题十
例10 已知方程
表示椭圆，求
的取值范围．
分析：根据椭圆方程的特征求解．
解：由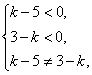
得
，且
．
∴满足条件的的取值范围是，且．
说明：本题易出现如下错解：由
得，故的取值范围是．出错的原因是没有注意椭圆的标准方程中
这个条件，当
时，并不表示椭圆．
典型例题十一
例11 已知
表示焦点在轴上的椭圆，求的取值范围．
分析：依据已知条件确定的三角函数的大小关系．再根据三角函数的单调性，求出的取值范围．
解：方程可化为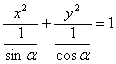
．
因为焦点在轴上，所以
．
因此
且
从而
．
说明：
(1)由椭圆的标准方程知
，
，这是容易忽视的地方．
(2)由焦点在轴上，知
，
．
(3)求的取值范围时，应注意题目中的条件
．
典型例题十二
例2 求中心在原点，对称轴为坐标轴，且经过
和
两点的椭圆方程．
分析：由题设条件焦点在哪个轴上不明确，椭圆标准方程有两种情形，为了计算简便起见，可设其方程为
(
，
)，且不必去考虑焦点在哪个坐标轴上，直接可求出方程．
解：设所求椭圆方程为(，)．
由和两点在椭圆上可得
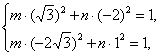即
所以
，
．
故所求的椭圆方程为
．
说明：此类题目中已存在直角坐标系，所以就不用建立直角坐标系了，但是这种题目一定要注意已知点和已知轨迹在坐标系中的位置关系．求椭圆的标准方程，一般是先定位（焦点位置），再定量（，的值），若椭圆的焦点位置确定，椭圆方程唯一；若椭圆的焦点位置不确定，既可能在轴，又可能在轴上，那么就分两种情况进行讨论．方法是待定系数法求椭圆的标准方程，求解时是分为根据椭圆的焦点在轴上或轴上确定方程的形式、根据题设条件列出关于待定系数，的方程组、解方程组求出，的值三个步骤，从而得到椭圆的标准方程．对此题而言，根据题目的要求不能判断出所求的椭圆焦点所在的坐标轴，那么就分情况讨论，这种方法解此题较繁．另一种方法直接设出椭圆的方程，而不强调焦点在哪一个坐标轴上，即不强调
和
的系数哪一个大，通过解题，解得几种情况就是几种情况．在求椭圆方程确定焦点在哪一坐标轴上的时候，可以根据焦点坐标，也可以根据准线方程．若不能确定焦点在哪一个坐标轴上，就用上述两种方法．
典型例题十三
例13 已知长轴为12，短轴长为6，焦点在轴上的椭圆，过它对的左焦点作倾斜解为
的直线交椭圆于，两点，求弦的长．
分析：此类题目是求弦长问题，这种题目方法很多，可以利用弦长公式
求得，也可以利用椭圆定义及余弦定理，还可以利用焦点半径来求．
解：(法1)利用直线与椭圆相交的弦长公式求解．
．
因为
，
，所以
．
又因为焦点在轴上，
所以椭圆方程为
，左焦点
，从而直线方程为
．
由直线方程与椭圆方程联立得
．
设
，为方程两根，
所以
，
，
，
从而
．
(法2)利用椭圆的定义及余弦定理求解．
由题意可知椭圆方程为，设
，
，则
，
．
在
中，
，
即
；
所以
．同理在
中，用余弦定理得
，所以
．
(法3)利用焦半径求解．
先根据直线与椭圆联立的方程求出方程的两根，，它们分别是，的横坐标．
再根据焦半径
，
，从而求出
．
说明：对于直线与椭圆的位置关系有相交、相切、相离，判断直线与椭圆的位置关系，可以利用直线方程与椭圆方程联立，看联立后方程解的个数：
，无解则相离；
，一解则相切；
，两解则相交．直线与椭圆相交就有直线与椭圆相交弦问题，直线与椭圆的两交点之间的线段叫做直线与椭圆相交弦．
典型例题十四
例14 已知圆
，从这个圆上任意一点向轴作垂线段，求线段中点的轨迹．
分析：本题是已知一些轨迹，求动点轨迹问题．这种题目一般利用中间变量(相关点)求轨迹方程或轨迹．
解：设点的坐标为
，点的坐标为
，
则
，
．
因为
在圆上，
所以
．
将
，
代入方程得
．
所以点的轨迹是一个椭圆．
说明：此题是利用相关点法求轨迹方程的方法，这种方法具体做法如下：首先设动点的坐标为，设已知轨迹上的点的坐标为，然后根据题目要求，使，与
，
建立等式关系，从而由这些等式关系求出和代入已知的轨迹方程，就可以求出关于，的方程，化简后即我们所求的方程．这种方法是求轨迹方程的最基本的方法，必须掌握．
这种题目还要注意题目的问法，是求“轨迹”还是求“轨迹方程”．若求轨迹方程，只要求出关于，的关系化简即可；若求轨迹，当求出轨迹方程后，还要说明由这种方程所确定的轨迹是什么．这在审题时要注意．
典型例题十五
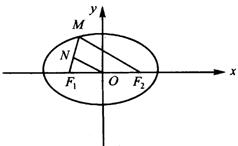
例15 椭圆
上的点到焦点的距离为2，
为
的中点，则
（为坐标原点）的值为( )
A．4 B．2 C．8 D．
解：如图所示，设椭圆的另一个焦点为，由椭圆第一定义得
，所以
，又因为
为
的中位线，所以
，故答案为A．
说明：
(1)椭圆定义：平面内与两定点的距离之和等于常数（大于
）的点的轨迹叫做椭圆．
(2)椭圆上的点必定适合椭圆的这一定义，即
，利用这个等式可以解决椭圆上的点与焦点的有关距离．
典型例题十六
例16 已知椭圆
，试确定的取值范围，使得对于直线
，椭圆上有不同的两点关于该直线对称．
分析：若设椭圆上，两点关于直线
对称，则已知条件等价于：(1)直线
；(2)弦的中点在上．利用上述条件建立的不等式即可求得的取值范围．
解：(法1)设椭圆上
，
两点关于直线对称，直线与交于
点．
∵的斜率
，
∴设直线的方程为
．
由方程组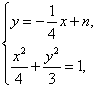
消去得
①
∴
．
于是
，
，
即点的坐标为
．
∵点在直线
上，∴
．
解得
． ②
将式②代入式①得
③
∵，是椭圆上的两点，∴
．
解得
．
(法2)同解法1得出，∴
，
，即点坐标为
．
∵，为椭圆上的两点，∴点在椭圆的内部，
∴
．
解得．
(法3)设，是椭圆上关于对称的两点，直线与的交点的坐标为
．
∵，在椭圆上，∴
，
．
两式相减得
，
即
．
∴
．
又∵直线，∴
，∴
，
即
①
又点在直线上，∴
②
由①，②得点的坐标为．
以下同解法2.
说明：涉及椭圆上两点，关于直线恒对称，求有关参数的取值范围问题，可以采用以下方法列参数满足的不等式：
(1)利用直线与椭圆恒有两个交点，通过直线方程与椭圆方程组成的方程组，消元后得到的一元二次方程的判别式，建立参数方程．
(2)利用弦的中点在椭圆内部，
，
满足不等式
，将，利用参数表示，建立参数不等式．
典型例题十七
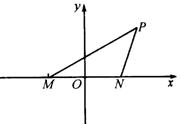
例17 在面积为1的
中，
，
，建立适当的坐标系，求出以、为焦点且过点的椭圆方程．
分析：本题考查用待定系数法求椭圆方程及适当坐标系的建立．通过适当坐标系的建立，选择相应椭圆方程，再待定系数．适当坐标系的建立能达到简化问题的目的．
解：以的中点为原点，所在直线为轴建立直角坐标系，设
．
则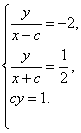
∴
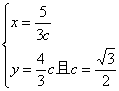
即
，∴
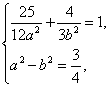得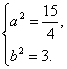
∴所求椭圆方程为
．
说明：适当坐标系的建立是处理好椭圆应用问题的关键．建立适当坐标系，需对题设所给图形进行观察、分析，做好数与形的结合，本题也可以以的中点为原点，所在直线为轴建立直角坐标系，再求椭圆方程．
典型例题十八
例18 已知
是直线被椭圆所截得的线段的中点，求直线的方程．
分析：本题考查直线与椭圆的位置关系问题．通常将直线方程与椭圆方程联立消去(或)，得到关于(或)的一元二次方程，再由根与系数的关系，直接求出
，
(或
，
)的值代入计算即得．并不需要求出直线与椭圆的交点坐标，这种“设而不求”的方法，在解析几何中是经常采用的．本题涉及到直线被椭圆截得弦的中点问题，也可采用点差法或中点坐标公式，运算会更为简便．
解：
方法一：设所求直线方程为
．
代入椭圆方程，整理得
①
设直线与椭圆的交点为，，则、是①的两根，∴
∵为中点，∴
，
．
∴所求直线方程为
．
方法二：设直线与椭圆交点，．∵为中点，∴
，
．又∵，在椭圆上，∴
，
两式相减得
，
即
．
∴
．
∴所求直线方程为．
方法三：设所求直线与椭圆的一个交点为
，另一个交点
．
∵、在椭圆上，∴
①
②
从而，在方程①－②的图形上，而过、的直线只有一条，
∴所求直线方程为．
说明：直线与圆锥曲线的位置关系是高考重点考查的解析几何问题，“设而不求”的方法是处理此类问题的有效方法．若已知焦点是
、
的椭圆截直线所得弦中点的横坐标是4，则如何求椭圆方程？