典型例题一
例1
椭圆的一个顶点为![]() ,其长轴长是短轴长的2倍,求椭圆的标准方程.
,其长轴长是短轴长的2倍,求椭圆的标准方程.
分析:题目没有指出焦点的位置,要考虑两种位置.
解:(1)当![]() 为长轴端点时,
为长轴端点时,![]() ,
,![]() ,
,
椭圆的标准方程为:![]() ;
;
(2)当![]() 为短轴端点时,
为短轴端点时,![]() ,
,![]() ,
,
椭圆的标准方程为:![]() ;
;
说明:椭圆的标准方程有两个,给出一个顶点的坐标和对称轴的位置,是不能确定椭圆的横竖的,因而要考虑两种情况.
典型例题二
例2 一个椭圆的焦点将其准线间的距离三等分,求椭圆的离心率.
解:![]() ∴
∴![]() ,
,
∴![]() .
.
说明:求椭圆的离心率问题,通常有两种处理方法,一是求![]() ,求
,求![]() ,再求比.二是列含
,再求比.二是列含![]() 和
和![]() 的齐次方程,再化含
的齐次方程,再化含![]() 的方程,解方程即可.
的方程,解方程即可.
典型例题三
例3 已知中心在原点,焦点在![]() 轴上的椭圆与直线
轴上的椭圆与直线![]() 交于
交于![]() 、
、![]() 两点,
两点,![]() 为
为![]() 中点,
中点,![]() 的斜率为0.25,椭圆的短轴长为2,求椭圆的方程.
的斜率为0.25,椭圆的短轴长为2,求椭圆的方程.
解:由题意,设椭圆方程为![]() ,
,
由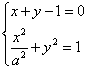 ,得
,得![]() ,
,
∴![]() ,
,![]() ,
,
![]() ,∴
,∴![]() ,
,
∴![]() 为所求.
为所求.
说明:(1)此题求椭圆方程采用的是待定系数法;(2)直线与曲线的综合问题,经常要借用根与系数的关系,来解决弦长、弦中点、弦斜率问题.
典型例题四
例4椭圆![]() 上不同三点
上不同三点![]() ,
,![]() ,
,![]() 与焦点
与焦点![]() 的距离成等差数列.
的距离成等差数列.
(1)求证![]() ;
;
(2)若线段![]() 的垂直平分线与
的垂直平分线与![]() 轴的交点为
轴的交点为![]() ,求直线
,求直线![]() 的斜率
的斜率![]() .
.
证明:(1)由椭圆方程知![]() ,
,![]() ,
,![]() .
.
由圆锥曲线的统一定义知: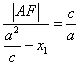 ,
,
∴ ![]() .
.
同理 ![]() .
.
∵ ![]() ,且
,且![]() ,
,
∴ ![]() ,
,
即 ![]() .
.
(2)因为线段![]() 的中点为
的中点为![]() ,所以它的垂直平分线方程为
,所以它的垂直平分线方程为
![]() .
.
又∵点![]() 在
在![]() 轴上,设其坐标为
轴上,设其坐标为![]() ,代入上式,得
,代入上式,得
![]()
又∵点![]() ,
,![]() 都在椭圆上,
都在椭圆上,
∴ ![]()
![]()
∴ ![]() .
.
将此式代入①,并利用![]() 的结论得
的结论得
![]()
∴ 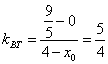 .
.
典型例题五
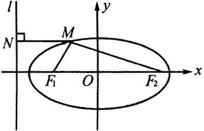 例5 已知椭圆
例5 已知椭圆![]() ,
,![]() 、
、![]() 为两焦点,问能否在椭圆上找一点
为两焦点,问能否在椭圆上找一点![]() ,使
,使![]() 到左准线
到左准线![]() 的距离
的距离![]() 是
是![]() 与
与![]() 的等比中项?若存在,则求出点
的等比中项?若存在,则求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
解:假设![]() 存在,设
存在,设![]() ,由已知条件得
,由已知条件得
![]() ,
,![]() ,∴
,∴![]() ,
,![]() .
.
∵左准线![]() 的方程是
的方程是![]() ,
,
∴![]() .
.
又由焦半径公式知:
![]() ,
,
![]() .
.
∵![]() ,
,
∴![]() .
.
整理得![]() .
.
解之得![]() 或
或![]() .
①
.
①
另一方面![]() .
②
.
②
则①与②矛盾,所以满足条件的点![]() 不存在.
不存在.
说明:
(1)利用焦半径公式解常可简化解题过程.
(2)本例是存在性问题,解决存在性问题,一般用分析法,即假设存在,根据已知条件进行推理和运算.进而根据推理得到的结果,再作判断.
(3)本例也可设![]() 存在,推出矛盾结论(读者自己完成).
存在,推出矛盾结论(读者自己完成).
典型例题六
例6 已知椭圆![]() ,求过点
,求过点![]() 且被
且被![]() 平分的弦所在的直线方程.
平分的弦所在的直线方程.
分析一:已知一点求直线,关键是求斜率,故设斜率为![]() ,利用条件求
,利用条件求![]() .
.
解法一:设所求直线的斜率为![]() ,则直线方程为
,则直线方程为![]() .代入椭圆方程,并整理得
.代入椭圆方程,并整理得
![]() .
.
由韦达定理得![]() .
.
∵![]() 是弦中点,∴
是弦中点,∴![]() .故得
.故得![]() .
.
所以所求直线方程为![]() .
.
分析二:设弦两端坐标为![]() 、
、![]() ,列关于
,列关于![]() 、
、![]() 、
、![]() 、
、![]() 的方程组,从而求斜率:
的方程组,从而求斜率:![]() .
.
解法二:设过![]() 的直线与椭圆交于
的直线与椭圆交于![]() 、
、![]() ,则由题意得
,则由题意得
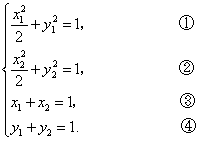
①-②得![]() .
⑤
.
⑤
将③、④代入⑤得![]() ,即直线的斜率为
,即直线的斜率为![]() .
.
所求直线方程为![]() .
.
说明:
(1)有关弦中点的问题,主要有三种类型:过定点且被定点平分的弦;平行弦的中点轨迹;过定点的弦中点轨迹.
(2)解法二是“点差法”,解决有关弦中点问题的题较方便,要点是巧代斜率.
(3)有关弦及弦中点问题常用的方法是:“韦达定理应用”及“点差法”.有关二次曲线问题也适用.
典型例题七
例7 求适合条件的椭圆的标准方程.
(1)长轴长是短轴长的2倍,且过点![]() ;
;
(2)在![]() 轴上的一个焦点与短轴两端点的联机互相垂直,且焦距为6.
轴上的一个焦点与短轴两端点的联机互相垂直,且焦距为6.
分析:当方程有两种形式时,应分别求解,如(1)题中由![]() 求出
求出![]() ,
,![]() ,在得方程
,在得方程![]() 后,不能依此写出另一方程
后,不能依此写出另一方程![]() .
.
解:(1)设椭圆的标准方程为![]() 或
或![]() .
.
由已知![]() .
①
.
①
又过点![]() ,因此有
,因此有
![]() 或
或![]() .
②
.
②
由①、②,得![]() ,
,![]() 或
或![]() ,
,![]() .故所求的方程为
.故所求的方程为
![]() 或
或![]() .
.
(2)设方程为![]() .由已知,
.由已知,![]() ,
,![]() ,所以
,所以![]() .故所求方程为
.故所求方程为![]() .
.
说明:根据条件求椭圆的标准方程的思路是“选标准,定参数”.关键在于焦点的位置是否确定,若不能确定,应设方程![]() 或
或![]() .
.
典型例题八
例8 椭圆![]() 的右焦点为
的右焦点为![]() ,过点
,过点![]() ,点
,点![]() 在椭圆上,当
在椭圆上,当![]() 为最小值时,求点
为最小值时,求点![]() 的坐标.
的坐标.
分析:本题的关键是求出离心率![]() ,把
,把![]() 转化为
转化为![]() 到右准线的距离,从而得最小值.一般地,求
到右准线的距离,从而得最小值.一般地,求![]() 均可用此法.
均可用此法.
 解:由已知:
解:由已知:![]() ,
,![]() .所以
.所以![]() ,右准线
,右准线![]() .
.
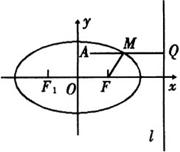
过![]() 作
作![]() ,垂足为
,垂足为![]() ,交椭圆于
,交椭圆于![]() ,故
,故![]() .显然
.显然![]() 的最小值为
的最小值为![]() ,即
,即![]() 为所求点,因此
为所求点,因此![]() ,且
,且![]() 在椭圆上.故
在椭圆上.故![]() .所以
.所以![]() .
.
说明:本题关键在于未知式![]() 中的“2”的处理.事实上,如图,
中的“2”的处理.事实上,如图,![]() ,即
,即![]() 是
是![]() 到右准线的距离的一半,即图中的
到右准线的距离的一半,即图中的![]() ,问题转化为求椭圆上一点
,问题转化为求椭圆上一点![]() ,使
,使![]() 到
到![]() 的距离与到右准线距离之和取最小值.
的距离与到右准线距离之和取最小值.
典型例题九
例9 求椭圆![]() 上的点到直线
上的点到直线![]() 的距离的最小值.
的距离的最小值.
分析:先写出椭圆的参数方程,由点到直线的距离建立三角函数关系式,求出距离的最小值.
解:椭圆的参数方程为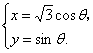 设椭圆上的点的坐标为
设椭圆上的点的坐标为![]() ,则点到直线的距离为
,则点到直线的距离为
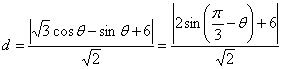 .
.
当![]() 时,
时,![]() .
.
说明:当直接设点的坐标不易解决问题时,可建立曲线的参数方程.
典型例题十
例10 设椭圆的中心是坐标原点,长轴在![]() 轴上,离心率
轴上,离心率![]() ,已知点
,已知点![]() 到这个椭圆上的点的最远距离是
到这个椭圆上的点的最远距离是![]() ,求这个椭圆的方程,并求椭圆上的点
,求这个椭圆的方程,并求椭圆上的点![]() 的距离等于
的距离等于![]() 的点的坐标.
的点的坐标.
分析:本题考查椭圆的性质、距离公式、最大值以及分析问题的能力,在求![]() 的最大值时,要注意讨论
的最大值时,要注意讨论![]() 的取值范围.此题可以用椭圆的标准方程,也可用椭圆的参数方程,要善于应用不等式、平面几何、三角等知识解决一些综合性问题,从而加强等价转换、形数结合的思想,提高逻辑推理能力.
的取值范围.此题可以用椭圆的标准方程,也可用椭圆的参数方程,要善于应用不等式、平面几何、三角等知识解决一些综合性问题,从而加强等价转换、形数结合的思想,提高逻辑推理能力.
解法一:设所求椭圆的直角坐标方程是![]() ,其中
,其中![]() 待定.
待定.
由![]() 可得
可得
![]() ,即
,即![]() .
.
设椭圆上的点![]() 到点
到点![]() 的距离是
的距离是![]() ,则
,则
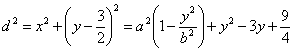
![]()
其中![]() .
.
如果![]() ,则当
,则当![]() 时,
时,![]() (从而
(从而![]() )有最大值.
)有最大值.
由题设得![]() ,由此得
,由此得![]() ,与
,与![]() 矛盾.
矛盾.
因此必有![]() 成立,于是当
成立,于是当![]() 时,
时,![]() (从而
(从而![]() )有最大值.
)有最大值.
由题设得![]() ,可得
,可得![]() ,
,![]() .
.
∴所求椭圆方程是![]() .
.
由![]() 及求得的椭圆方程可得,椭圆上的点
及求得的椭圆方程可得,椭圆上的点![]() ,点
,点![]() 到点
到点![]() 的距离是
的距离是![]() .
.
解法二:根据题设条件,可取椭圆的参数方程是![]() ,其中
,其中![]() ,待定,
,待定,![]() ,
,![]() 为参数.
为参数.
由![]() 可得
可得
![]() ,即
,即![]() .
.
设椭圆上的点![]() 到点
到点![]() 的距离为
的距离为![]() ,则
,则
![]()
![]()
![]()
如果![]() ,即
,即![]() ,则当
,则当![]() 时,
时,![]() (从而
(从而![]() )有最大值.
)有最大值.
由题设得![]() ,由此得
,由此得![]() ,与
,与![]() 矛盾,因此必有
矛盾,因此必有![]() 成立.
成立.
于是当![]() 时
时![]() (从而
(从而![]() )有最大值.
)有最大值.
由题设知![]() ,∴
,∴![]() ,
,![]() .
.
∴所求椭圆的参数方程是![]() .
.
由![]() ,
,![]() ,可得椭圆上的是
,可得椭圆上的是![]() ,
,![]() .
.
典型例题十一
例11 设![]() ,
,![]() ,
,![]() ,求
,求![]() 的最大值和最小值.
的最大值和最小值.
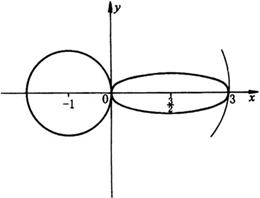
分析:本题的关键是利用形数结合,观察方程![]() 与椭圆方程的结构一致.设
与椭圆方程的结构一致.设![]() ,显然它表示一个圆,由此可以画出图形,考虑椭圆及圆的位置关系求得最值.
,显然它表示一个圆,由此可以画出图形,考虑椭圆及圆的位置关系求得最值.
解:由![]() ,得
,得
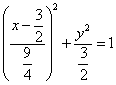
可见它表示一个椭圆,其中心在![]() 点,焦点在
点,焦点在![]() 轴上,且过(0,0)点和(3,0)点.
轴上,且过(0,0)点和(3,0)点.
设![]() ,则
,则
![]()
它表示一个圆,其圆心为(-1,0)半径为![]() .
.
在同一坐标系中作出椭圆及圆,如图所示.观察图形可知,当圆过(0,0)点时,半径最小,即![]() ,此时
,此时![]() ;当圆过(3,0)点时,半径最大,即
;当圆过(3,0)点时,半径最大,即![]() ,∴
,∴![]() .
.
∴![]() 的最小值为0,最大值为15.
的最小值为0,最大值为15.
典型例题十二
例12 已知椭圆![]() ,
,![]() 、
、![]() 是其长轴的两个端点.
是其长轴的两个端点.
(1)过一个焦点![]() 作垂直于长轴的弦
作垂直于长轴的弦![]() ,求证:不论
,求证:不论![]() 、
、![]() 如何变化,
如何变化,![]() .
.
(2)如果椭圆上存在一个点![]() ,使
,使![]() ,求
,求![]() 的离心率
的离心率![]() 的取值范围.
的取值范围.
分析:本题从已知条件出发,两问都应从![]() 和
和![]() 的正切值出发做出估计,因此要从点的坐标、斜率入手.本题的第(2)问中,其关键是根据什么去列出离心率
的正切值出发做出估计,因此要从点的坐标、斜率入手.本题的第(2)问中,其关键是根据什么去列出离心率![]() 满足的不等式,只能是椭圆的固有性质:
满足的不等式,只能是椭圆的固有性质:![]() ,
,![]() ,根据
,根据![]() 得到
得到![]() ,将
,将![]() 代入,消去
代入,消去![]() ,用
,用![]() 、
、![]() 、
、![]() 表示
表示![]() ,以便利用
,以便利用![]() 列出不等式.这里要求思路清楚,计算准确,一气呵成.
列出不等式.这里要求思路清楚,计算准确,一气呵成.
解:(1)设![]() ,
,![]() ,
,![]() .
.
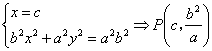
于是![]() ,
,![]() .
.
∵![]() 是
是![]() 到
到![]() 的角.
的角.
∴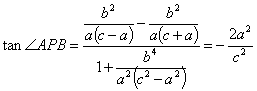
∵![]()
∴![]()
故![]() ∴
∴![]() .
.
(2)设![]() ,则
,则![]() ,
,![]() .
.
由于对称性,不妨设![]() ,于是
,于是![]() 是
是![]() 到
到![]() 的角.
的角.
∴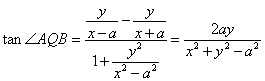
∵![]() , ∴
, ∴![]()
整理得![]()
∵![]()
∴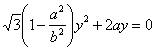
∵![]() , ∴
, ∴![]()
∵![]() , ∴
, ∴![]()
![]() ,
,![]()
∴![]() ,
,![]()
∴![]() 或
或![]() (舍),∴
(舍),∴![]() .
.
典型例题十三
例13 已知椭圆![]() 的离心率
的离心率![]() ,求
,求![]() 的值.
的值.
分析:分两种情况进行讨论.
解:当椭圆的焦点在![]() 轴上时,
轴上时,![]() ,
,![]() ,得
,得![]() .由
.由![]() ,得
,得![]() .
.
当椭圆的焦点在![]() 轴上时,
轴上时,![]() ,
,![]() ,得
,得![]() .
.
由![]() ,得
,得![]() ,即
,即![]() .
.
∴满足条件的![]() 或
或![]() .
.
说明:本题易出现漏解.排除错误的办法是:因为![]() 与9的大小关系不定,所以椭圆的焦点可能在
与9的大小关系不定,所以椭圆的焦点可能在![]() 轴上,也可能在
轴上,也可能在![]() 轴上.故必须进行讨论.
轴上.故必须进行讨论.
典型例题十四
例14 已知椭圆![]() 上一点
上一点![]() 到右焦点
到右焦点![]() 的距离为
的距离为![]()
![]() ,求
,求![]() 到左准线的距离.
到左准线的距离.
分析:利用椭圆的两个定义,或利用第二定义和椭圆两准线的距离求解.
解法一:由![]() ,得
,得![]() ,
,![]() ,
,![]() .
.
由椭圆定义,![]() ,得
,得
![]() .
.
由椭圆第二定义,![]() ,
,![]() 为
为![]() 到左准线的距离,
到左准线的距离,
∴![]() ,
,
即![]() 到左准线的距离为
到左准线的距离为![]() .
.
解法二:∵![]() ,
,![]() 为
为![]() 到右准线的距离,
到右准线的距离,![]() ,
,
∴![]() .
.
又椭圆两准线的距离为![]() .
.
∴![]() 到左准线的距离为
到左准线的距离为![]() .
.
说明:运用椭圆的第二定义时,要注意焦点和准线的同侧性.否则就会产生误解.
椭圆有两个定义,是从不同的角度反映椭圆的特征,解题时要灵活选择,运用自如.一般地,如遇到动点到两个定点的问题,用椭圆第一定义;如果遇到动点到定直线的距离问题,则用椭圆的第二定义.
典型例题十五
例15 设椭圆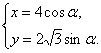 (
(![]() 为参数)上一点
为参数)上一点![]() 与
与![]() 轴正向所成角
轴正向所成角![]() ,求
,求![]() 点坐标.
点坐标.
分析:利用参数![]() 与
与![]() 之间的关系求解.
之间的关系求解.
解:设![]() ,由
,由![]() 与
与![]() 轴正向所成角为
轴正向所成角为![]() ,
,
∴![]() ,即
,即![]() .
.
而![]() ,
,![]() ,由此得到
,由此得到![]() ,
,![]() ,
,
∴![]() 点坐标为
点坐标为![]() .
.
典型例题十六
例16 设![]() 是离心率为
是离心率为![]() 的椭圆
的椭圆![]()
![]() 上的一点,
上的一点,![]() 到左焦点
到左焦点![]() 和右焦点
和右焦点![]() 的距离分别为
的距离分别为![]() 和
和![]() ,求证:
,求证:![]() ,
,![]() .
.
分析:本题考查椭圆的两个定义,利用椭圆第二定义,可将椭圆上点到焦点的距离转化为点到相应准线距离.
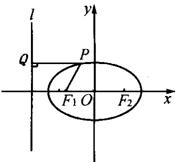
解:![]() 点到椭圆的左准线
点到椭圆的左准线![]() 的距离,
的距离,![]() ,
,
由椭圆第二定义,![]() ,
,
∴![]() ,由椭圆第一定义,
,由椭圆第一定义,![]() .
.
说明:本题求证的是椭圆的焦半径公式,在解决与椭圆的焦半径(或焦点弦)的有关问题时,有着广泛的应用.请写出椭圆焦点在![]() 轴上的焦半径公式.
轴上的焦半径公式.
典型例题十七
例17 已知椭圆![]() 内有一点
内有一点![]() ,
,![]() 、
、![]() 分别是椭圆的左、右焦点,点
分别是椭圆的左、右焦点,点![]() 是椭圆上一点.
是椭圆上一点.
(1) 求![]() 的最大值、最小值及对应的点
的最大值、最小值及对应的点![]() 坐标;
坐标;
(2) 求![]() 的最小值及对应的点
的最小值及对应的点![]() 的坐标.
的坐标.
分析:本题考查椭圆中的最值问题,通常探求变量的最值有两种方法:一是目标函数当,即代数方法.二是数形结合,即几何方法.本题若按先建立目标函数,再求最值,则不易解决;若抓住椭圆的定义,转化目标,运用数形结合,就能简捷求解.
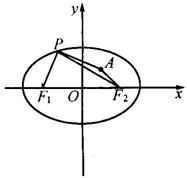
解:
(1)如上图,![]() ,
,![]() ,
,![]() ,设
,设![]() 是椭圆上任一点,由
是椭圆上任一点,由![]() ,
,![]() ,∴
,∴![]() ,等号仅当
,等号仅当![]() 时成立,此时
时成立,此时![]() 、
、![]() 、
、![]() 共线.
共线.
由![]() ,∴
,∴![]() ,等号仅当
,等号仅当![]() 时成立,此时
时成立,此时![]() 、
、![]() 、
、![]() 共线.
共线.
建立![]() 、
、![]() 的直线方程
的直线方程![]() ,解方程组
,解方程组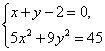 得两交点
得两交点
![]() 、
、![]() .
.
综上所述,![]() 点与
点与![]() 重合时,
重合时,![]() 取最小值
取最小值![]() ,
,![]() 点与
点与![]() 重合时,
重合时,![]() 取最大值
取最大值![]() .
.
(2)如下图,设![]() 是椭圆上任一点,作
是椭圆上任一点,作![]() 垂直椭圆右准线,
垂直椭圆右准线,![]() 为垂足,由
为垂足,由![]() ,
,![]() ,∴
,∴![]() .由椭圆第二定义知
.由椭圆第二定义知![]() ,∴
,∴![]() ,∴
,∴![]() ,要使其和最小需有
,要使其和最小需有![]() 、
、![]() 、
、![]() 共线,即求
共线,即求![]() 到右准线距离.右准线方程为
到右准线距离.右准线方程为![]() .
.
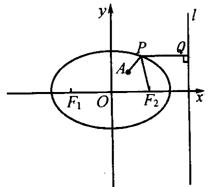
∴![]() 到右准线距离为
到右准线距离为![]() .此时
.此时![]() 点纵坐标与
点纵坐标与![]() 点纵坐标相同为1,代入椭圆得满足条件的点
点纵坐标相同为1,代入椭圆得满足条件的点![]() 坐标
坐标![]() .
.
说明:求![]() 的最小值,就是用第二定义转化后,过
的最小值,就是用第二定义转化后,过![]() 向相应准线作垂线段.巧用焦点半径
向相应准线作垂线段.巧用焦点半径![]() 与点准距
与点准距![]() 互化是解决有关问题的重要手段.
互化是解决有关问题的重要手段.
典型例题十八
例18 (1)写出椭圆![]() 的参数方程;
的参数方程;
(2)求椭圆内接矩形的最大面积.
分析:本题考查椭圆的参数方程及其应用.为简化运算和减少未知数的个数,常用椭圆的参数方程表示曲线上一点坐标,所求问题便化归为三角问题.
解:(1) ![]()
![]() .
.
(2)设椭圆内接矩形面积为![]() ,由对称性知,矩形的邻边分别平行于
,由对称性知,矩形的邻边分别平行于![]() 轴和
轴和![]() 轴,设
轴,设![]() 为矩形在第一象限的顶点,
为矩形在第一象限的顶点,![]() ,
,
则![]()
故椭圆内接矩形的最大面积为12.
说明:通过椭圆参数方程,转化为三角函数的最值问题,一般地,与圆锥曲线有关的最值问题,用参数方程形式较简便.
典型例题十九
例19 已知![]() ,
,![]() 是椭圆的两个焦点,
是椭圆的两个焦点,![]() 是椭圆上一点,且
是椭圆上一点,且![]() .
.
(1)求椭圆离心率的取值范围;
(2)求证![]() 的面积与椭圆短轴长有关.
的面积与椭圆短轴长有关.
分析:不失一般性,可以设椭圆方程为
![]() (
(![]() ),
),![]() (
(![]() ).
).
思路一:根据题设容易想到两条直线的夹角公式,即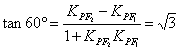 ,设
,设![]() ,
,![]() ,
,![]() ,化简可得
,化简可得![]() .又
.又![]() ,两方程联立消去
,两方程联立消去![]() 得
得![]() ,由
,由![]() ,可以确定离心率的取值范围;解出
,可以确定离心率的取值范围;解出![]() 可以求出
可以求出![]() 的面积,但这一过程很繁.
的面积,但这一过程很繁.
思路二:利用焦半径公式![]() ,
,![]() ,在
,在![]() 中运用余弦定理,求
中运用余弦定理,求![]() ,再利用
,再利用![]() ,可以确定离心率
,可以确定离心率![]() 的取值范围,将
的取值范围,将![]() 代入椭圆方程中求
代入椭圆方程中求![]() ,便可求出
,便可求出![]() 的面积.
的面积.
思路三:利用正弦定理、余弦定理,结合![]() 求解.
求解.
解:(法1)设椭圆方程为![]() (
(![]() ),
),![]() ,
,![]() ,
,![]() ,
,![]() ,
,
则![]() ,
,![]() .
.
在![]() 中,由余弦定理得
中,由余弦定理得
![]() ,
,
解得![]() .
.
(1)∵![]() ,
,
∴![]() ,即
,即![]() .
.
∴![]() .
.
故椭圆离心率的取范围是![]() .
.
(2)将![]() 代入
代入![]() 得
得
![]() ,即
,即![]() .
.
∴![]() .
.
即![]() 的面积只与椭圆的短轴长有关.
的面积只与椭圆的短轴长有关.
(法2)设![]() ,
,![]() ,
,![]() ,
,![]() ,
,
则![]() .
.
(1)在![]() 中,由正弦定理得
中,由正弦定理得
![]() .
.
∴![]()
∵![]() ,
,
∴![]() ,
,
∴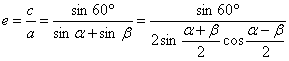
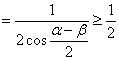 .
.
当且仅当![]() 时等号成立.
时等号成立.
故椭圆离心率的取值范围是![]() .
.
(2)在![]() 中,由余弦定理得:
中,由余弦定理得:
![]()
![]()
![]()
∵![]() ,
,
∴![]() ,即
,即![]() .
.
∴![]() .
.
即![]() 的面积与椭圆短轴长有关.
的面积与椭圆短轴长有关.
说明:椭圆上的一点![]() 与两个焦点
与两个焦点![]() ,
,![]() 构成的三角形为椭圆的焦点三角形,涉及有关焦点三角形问题,通常运用三角形的边角关系定理.解题中通过变形,使之出现
构成的三角形为椭圆的焦点三角形,涉及有关焦点三角形问题,通常运用三角形的边角关系定理.解题中通过变形,使之出现![]() 的结构,这样就可以应用椭圆的定义,从而可得到有关
的结构,这样就可以应用椭圆的定义,从而可得到有关![]() ,
,![]() 的关系式,使问题找到解决思路.
的关系式,使问题找到解决思路.
典型例题二十
例20 椭圆![]()
![]() 与
与![]() 轴正向交于点
轴正向交于点![]() ,若这个椭圆上总存在点
,若这个椭圆上总存在点![]() ,使
,使![]() (
(![]() 为坐标原点),求其离心率
为坐标原点),求其离心率![]() 的取值范围.
的取值范围.
分析:∵![]() 、
、![]() 为定点,
为定点,![]() 为动点,可以
为动点,可以![]() 点坐标作为参数,把
点坐标作为参数,把![]() ,转化为
,转化为![]() 点坐标的一个等量关系,再利用坐标的范围建立关于
点坐标的一个等量关系,再利用坐标的范围建立关于![]() 、
、![]() 、
、![]() 的一个不等式,转化为关于
的一个不等式,转化为关于![]() 的不等式.为减少参数,易考虑运用椭圆参数方程.
的不等式.为减少参数,易考虑运用椭圆参数方程.
解:设椭圆的参数方程是![]()
![]() ,
,
则椭圆上的点![]() ,
,![]() ,
,
∵![]() ,∴
,∴![]() ,
,
即![]() ,解得
,解得![]() 或
或![]() ,
,
∵![]() ∴
∴![]() (舍去),
(舍去),![]() ,又
,又![]()
∴![]() ,
,
∴![]() ,又
,又![]() ,∴
,∴![]() .
.
说明:若已知椭圆离心率范围![]() ,求证在椭圆上总存在点
,求证在椭圆上总存在点![]() 使
使![]() .如何证明?
.如何证明?