典型例题一
例1 圆![]() 上到直线
上到直线![]() 的距离为1的点有几个?
的距离为1的点有几个?
分析:借助图形直观求解.或先求出直线![]() 、
、![]() 的方程,从代数计算中寻找解答.
的方程,从代数计算中寻找解答.
解法一:圆![]() 的圆心为
的圆心为![]() ,半径
,半径![]() .
.
设圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() ,则
,则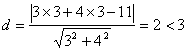 .
.
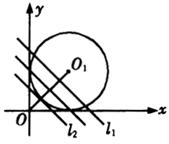
如图,在圆心![]() 同侧,与直线
同侧,与直线![]() 平行且距离为1的直线
平行且距离为1的直线![]() 与圆有两个交点,这两个交点符合题意.
与圆有两个交点,这两个交点符合题意.
又![]() .
.
∴与直线![]() 平行的圆的切线的两个切点中有一个切点也符合题意.
平行的圆的切线的两个切点中有一个切点也符合题意.
∴符合题意的点共有3个.
解法二:符合题意的点是平行于直线![]() ,且与之距离为1的直线和圆的交点.
,且与之距离为1的直线和圆的交点.
设所求直线为![]() ,则
,则![]() ,
,
∴![]() ,即
,即![]() ,或
,或![]() ,也即
,也即
![]() ,或
,或![]() .
.
设圆![]() 的圆心到直线
的圆心到直线![]() 、
、![]() 的距离为
的距离为![]() 、
、![]() ,则
,则
![]() ,
,![]() .
.
∴![]() 与
与![]() 相切,与圆
相切,与圆![]() 有一个公共点;
有一个公共点;![]() 与圆
与圆![]() 相交,与圆
相交,与圆![]() 有两个公共点.即符合题意的点共3个.
有两个公共点.即符合题意的点共3个.
说明:对于本题,若不留心,则易发生以下误解:
设圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() ,则
,则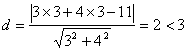 .
.
∴圆![]() 到
到![]() 距离为1的点有两个.
距离为1的点有两个.
显然,上述误解中的![]() 是圆心到直线
是圆心到直线![]() 的距离,
的距离,![]() ,只能说明此直线与圆有两个交点,而不能说明圆上有两点到此直线的距离为1.
,只能说明此直线与圆有两个交点,而不能说明圆上有两点到此直线的距离为1.
到一条直线的距离等于定值的点,在与此直线距离为这个定值的两条平行直线上,因此题中所求的点就是这两条平行直线与圆的公共点.求直线与圆的公共点个数,一般根据圆与直线的位置关系来判断,即根据圆心与直线的距离和半径的大小比较来判断.
典型例题三
例3 求过两点![]() 、
、![]() 且圆心在直线
且圆心在直线![]() 上的圆的标准方程并判断点
上的圆的标准方程并判断点![]() 与圆的关系.
与圆的关系.
分析:欲求圆的标准方程,需求出圆心坐标的圆的半径的大小,而要判断点![]() 与圆的位置关系,只须看点
与圆的位置关系,只须看点![]() 与圆心的距离和圆的半径的大小关系,若距离大于半径,则点在圆外;若距离等于半径,则点在圆上;若距离小于半径,则点在圆内.
与圆心的距离和圆的半径的大小关系,若距离大于半径,则点在圆外;若距离等于半径,则点在圆上;若距离小于半径,则点在圆内.
解法一:(待定系数法)
设圆的标准方程为![]() .
.
∵圆心在![]() 上,故
上,故![]() .
.
∴圆的方程为![]() .
.
又∵该圆过![]() 、
、![]() 两点.
两点.
∴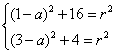
解之得:![]() ,
,![]() .
.
所以所求圆的方程为![]() .
.
解法二:(直接求出圆心坐标和半径)
因为圆过![]() 、
、![]() 两点,所以圆心
两点,所以圆心![]() 必在线段
必在线段![]() 的垂直平分线
的垂直平分线![]() 上,又因为
上,又因为![]() ,故
,故![]() 的斜率为1,又
的斜率为1,又![]() 的中点为
的中点为![]() ,故
,故![]() 的垂直平分线
的垂直平分线![]() 的方程为:
的方程为:![]() 即
即![]() .
.
又知圆心在直线![]() 上,故圆心坐标为
上,故圆心坐标为![]()
∴半径![]() .
.
故所求圆的方程为![]() .
.
又点![]() 到圆心
到圆心![]() 的距离为
的距离为
![]() .
.
∴点![]() 在圆外.
在圆外.
说明:本题利用两种方法求解了圆的方程,都围绕着求圆的圆心和半径这两个关键的量,然后根据圆心与定点之间的距离和半径的大小关系来判定点与圆的位置关系,若将点换成直线又该如何来判定直线与圆的位置关系呢?
典型例题四
例4 圆![]() 上到直线
上到直线![]() 的距离为
的距离为![]() 的点共有( ).
的点共有( ).
(A)1个 (B)2个 (C)3个 (D)4个
分析:把![]() 化为
化为![]() ,圆心为
,圆心为![]() ,半径为
,半径为![]() ,圆心到直线的距离为
,圆心到直线的距离为![]() ,所以在圆上共有三个点到直线的距离等于
,所以在圆上共有三个点到直线的距离等于![]() ,所以选C.
,所以选C.
典型例题五
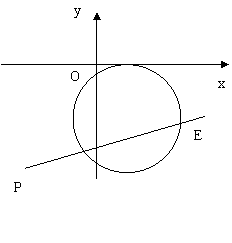
例5 过点![]() 作直线
作直线![]() ,当斜率为何值时,直线
,当斜率为何值时,直线![]() 与圆
与圆![]() 有公共点,如图所示.
有公共点,如图所示.
分析:观察动画演示,分析思路.
 解:设直线
解:设直线![]() 的方程为
的方程为
![]()
即
![]()
根据![]() 有
有
![]()
整理得
![]()
解得
![]() .
.
典型例题六
例6 已知圆![]() ,求过点
,求过点![]() 与圆
与圆![]() 相切的切线.
相切的切线.
解:∵点![]() 不在圆
不在圆![]() 上,
上,
∴切线![]() 的直线方程可设为
的直线方程可设为![]()
根据![]()
∴
![]()
解得
![]()
所以
![]()
即
![]()
因为过圆外一点作圆得切线应该有两条,可见另一条直线的斜率不存在.易求另一条切线为![]() .
.
说明:上述解题过程容易漏解斜率不存在的情况,要注意补回漏掉的解.
本题还有其他解法,例如把所设的切线方程代入圆方程,用判别式等于0解决(也要注意漏解).还可以运用![]() ,求出切点坐标
,求出切点坐标![]() 、
、![]() 的值来解决,此时没有漏解.
的值来解决,此时没有漏解.
典型例题七
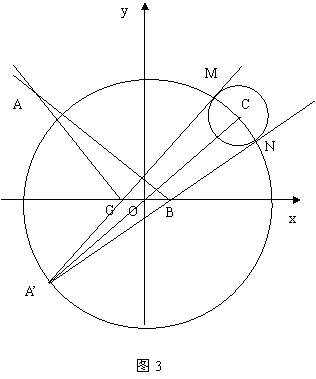
例7 自点![]() 发出的光线
发出的光线![]() 射到
射到![]() 轴上,被
轴上,被![]() 轴反射,反射光线所在的直线与圆
轴反射,反射光线所在的直线与圆![]() 相切
相切
(1)求光线![]() 和反射光线所在的直线方程.
和反射光线所在的直线方程.
 (2)光线自
(2)光线自![]() 到切点所经过的路程.
到切点所经过的路程.
分析、略解:观察动画演示,分析思路.根据对称关系,首先求出点![]() 的对称点
的对称点![]() 的坐标为
的坐标为![]() ,其次设过
,其次设过![]() 的圆
的圆![]() 的切线方程为
的切线方程为
![]()
根据![]() ,即求出圆
,即求出圆![]() 的切线的斜率为
的切线的斜率为
![]() 或
或![]()
进一步求出反射光线所在的直线的方程为
![]() 或
或![]()
最后根据入射光与反射光关于![]() 轴对称,求出入射光所在直线方程为
轴对称,求出入射光所在直线方程为
![]() 或
或![]()
光路的距离为![]() ,可由勾股定理求得
,可由勾股定理求得![]() .
.
说明:本题亦可把圆对称到![]() 轴下方,再求解.
轴下方,再求解.
典型例题八
例8 如图所示,已知圆![]() 与
与![]() 轴的正方向交于
轴的正方向交于![]() 点,点
点,点![]() 在直线
在直线![]() 上运动,过
上运动,过![]() 做圆
做圆![]() 的切线,切点为
的切线,切点为![]() ,求
,求![]() 垂心
垂心![]() 的轨迹.
的轨迹.
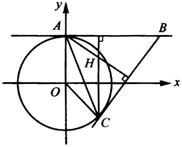
分析:按常规求轨迹的方法,设![]() ,找
,找![]() 的关系非常难.由于
的关系非常难.由于![]() 点随
点随![]() ,
,![]() 点运动而运动,可考虑
点运动而运动,可考虑![]() ,
,![]() ,
,![]() 三点坐标之间的关系.
三点坐标之间的关系.
解:设![]() ,
,![]() ,连结
,连结![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,![]() 是切线
是切线![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,
所以四边形![]() 是菱形.
是菱形.
所以![]() ,得
,得
又![]() 满足
满足![]() ,
,
所以![]() 即是所求轨迹方程.
即是所求轨迹方程.
说明:题目巧妙运用了三角形垂心的性质及菱形的相关知识.采取代入法求轨迹方程.做题时应注意分析图形的几何性质,求轨迹时应注意分析与动点相关联的点,如相关联点轨迹方程已知,可考虑代入法.
典型例题九
例9 求半径为4,与圆![]() 相切,且和直线
相切,且和直线![]() 相切的圆的方程.
相切的圆的方程.
分析:根据问题的特征,宜用圆的标准方程求解.
解:则题意,设所求圆的方程为圆![]() .
.
圆![]() 与直线
与直线![]() 相切,且半径为4,则圆心
相切,且半径为4,则圆心![]() 的坐标为
的坐标为![]() 或
或![]() .
.
又已知圆![]() 的圆心
的圆心![]() 的坐标为
的坐标为![]() ,半径为3.
,半径为3.
若两圆相切,则![]() 或
或![]() .
.
(1)当![]() 时,
时,![]() ,或
,或![]() (无解),故可得
(无解),故可得![]() .
.
∴所求圆方程为![]() ,或
,或![]() .
.
(2)当![]() 时,
时,![]() ,或
,或![]() (无解),故
(无解),故![]() .
.
∴所求圆的方程为![]() ,或
,或![]() .
.
说明:对本题,易发生以下误解:
由题意,所求圆与直线![]() 相切且半径为4,则圆心坐标为
相切且半径为4,则圆心坐标为![]() ,且方程形如
,且方程形如![]() .又圆
.又圆![]() ,即
,即![]() ,其圆心为
,其圆心为![]() ,半径为3.若两圆相切,则
,半径为3.若两圆相切,则![]() .故
.故![]() ,解之得
,解之得![]() .所以欲求圆的方程为
.所以欲求圆的方程为![]() ,或
,或![]() .
.
上述误解只考虑了圆心在直线![]() 上方的情形,而疏漏了圆心在直线
上方的情形,而疏漏了圆心在直线![]() 下方的情形.另外,误解中没有考虑两圆内切的情况.也是不全面的.
下方的情形.另外,误解中没有考虑两圆内切的情况.也是不全面的.
典型例题十
例10 已知圆![]() 与直线
与直线![]() 相交于
相交于![]() 、
、![]() 两点,
两点,![]() 为原点,且
为原点,且![]() ,求实数
,求实数![]() 的值.
的值.
分析:设![]() 、
、![]() 两点的坐标为
两点的坐标为![]() 、
、![]() ,则由
,则由![]() ,可得
,可得![]() ,再利用一元二次方程根与系数的关系求解.或因为通过原点的直线的斜率为
,再利用一元二次方程根与系数的关系求解.或因为通过原点的直线的斜率为![]() ,由直线
,由直线![]() 与圆的方程构造以
与圆的方程构造以![]() 为未知数的一元二次方程,由根与系数关系得出
为未知数的一元二次方程,由根与系数关系得出![]() 的值,从而使问题得以解决.
的值,从而使问题得以解决.
解法一:设点![]() 、
、![]() 的坐标为
的坐标为![]() 、
、![]() .一方面,由
.一方面,由![]() ,得
,得
![]() ,即
,即![]() ,也即:
,也即:![]() . ①
. ①
另一方面,![]() 、
、![]() 是方程组
是方程组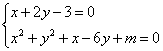 的实数解,即
的实数解,即![]() 、
、![]() 是方程
是方程![]() ②
②
的两个根.
∴![]() ,
,![]() . ③
. ③
又![]() 、
、![]() 在直线
在直线![]() 上,
上,
∴![]() .
.
将③代入,得![]() . ④
. ④
将③、④代入①,解得![]() ,代入方程②,检验
,代入方程②,检验![]() 成立,
成立,
∴![]() .
.
解法二:由直线方程可得![]() ,代入圆的方程
,代入圆的方程![]() ,有
,有
![]() ,
,
整理,得![]() .
.
由于![]() ,故可得
,故可得
![]() .
.
∴![]() ,
,![]() 是上述方程两根.故
是上述方程两根.故![]() .得
.得
![]() ,解得
,解得![]() .
.
经检验可知![]() 为所求.
为所求.
说明:求解本题时,应避免去求![]() 、
、![]() 两点的坐标的具体数值.除此之外,还应对求出的
两点的坐标的具体数值.除此之外,还应对求出的![]() 值进行必要的检验,这是因为在求解过程中并没有确保有交点
值进行必要的检验,这是因为在求解过程中并没有确保有交点![]() 、
、![]() 存在.
存在.
解法一显示了一种解这类题的通法,解法二的关键在于依据直线方程构造出一个关于![]() 的二次齐次方程,虽有规律可循,但需一定的变形技巧,同时也可看出,这种方法给人以一种淋漓酣畅,一气呵成之感.
的二次齐次方程,虽有规律可循,但需一定的变形技巧,同时也可看出,这种方法给人以一种淋漓酣畅,一气呵成之感.
典型例题十一
例11 求经过点![]() ,且与直线
,且与直线![]() 和
和![]() 都相切的圆的方程.
都相切的圆的方程.
分析:欲确定圆的方程.需确定圆心坐标与半径,由于所求圆过定点![]() ,故只需确定圆心坐标.又圆与两已知直线相切,故圆心必在它们的交角的平分线上.
,故只需确定圆心坐标.又圆与两已知直线相切,故圆心必在它们的交角的平分线上.
解:∵圆和直线![]() 与
与![]() 相切,
相切,
∴圆心![]() 在这两条直线的交角平分线上,
在这两条直线的交角平分线上,
又圆心到两直线![]() 和
和![]() 的距离相等.
的距离相等.
∴![]() .
.
∴两直线交角的平分线方程是![]() 或
或![]() .
.
又∵圆过点![]() ,
,
∴圆心![]() 只能在直线
只能在直线![]() 上.
上.
设圆心![]()
∵![]() 到直线
到直线![]() 的距离等于
的距离等于![]() ,
,
∴![]() .
.
化简整理得![]() .
.
解得:![]() 或
或![]()
∴圆心是![]() ,半径为
,半径为![]() 或圆心是
或圆心是![]() ,半径为
,半径为![]() .
.
∴所求圆的方程为![]() 或
或![]() .
.
说明:本题解决的关键是分析得到圆心在已知两直线的交角平分线上,从而确定圆心坐标得到圆的方程,这是过定点且与两已知直线相切的圆的方程的常规求法.
典型例题十二
例12 设圆满足:(1)截![]() 轴所得弦长为2;(2)被
轴所得弦长为2;(2)被![]() 轴分成两段弧,其弧长的比为
轴分成两段弧,其弧长的比为![]() ,在满足条件(1)(2)的所有圆中,求圆心到直线
,在满足条件(1)(2)的所有圆中,求圆心到直线![]() 的距离最小的圆的方程.
的距离最小的圆的方程.
分析:要求圆的方程,只须利用条件求出圆心坐标和半径,便可求得圆的标准方程.满足两个条件的圆有无数个,其圆心的集合可看作动点的轨迹,若能求出这轨迹的方程,便可利用点到直线的距离公式,通过求最小值的方法找到符合题意的圆的圆心坐标,进而确定圆的半径,求出圆的方程.
解法一:设圆心为![]() ,半径为
,半径为![]() .
.
则![]() 到
到![]() 轴、
轴、![]() 轴的距离分别为
轴的距离分别为![]() 和
和![]() .
.
由题设知:圆截![]() 轴所得劣弧所对的圆心角为
轴所得劣弧所对的圆心角为![]() ,故圆截
,故圆截![]() 轴所得弦长为
轴所得弦长为![]() .
.
∴![]()
又圆截![]() 轴所得弦长为2.
轴所得弦长为2.
∴![]() .
.
又∵![]() 到直线
到直线![]() 的距离为
的距离为
![]()
∴![]()
![]()
![]()
![]()
当且仅当![]() 时取“=”号,此时
时取“=”号,此时![]() .
.
这时有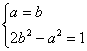
∴![]() 或
或![]()
又![]()
故所求圆的方程为![]() 或
或![]()
解法二:同解法一,得
![]() .
.
∴![]() .
.
∴![]() .
.
将![]() 代入上式得:
代入上式得:
![]() .
.
上述方程有实根,故
![]() ,
,
∴![]() .
.
将![]() 代入方程得
代入方程得![]() .
.
又![]() ∴
∴![]() .
.
由![]() 知
知![]() 、
、![]() 同号.
同号.
故所求圆的方程为![]() 或
或![]() .
.
说明:本题是求点到直线距离最小时的圆的方程,若变换为求面积最小呢?
典型例题十三
例13 两圆![]() 与
与![]() 相交于
相交于![]() 、
、![]() 两点,求它们的公共弦
两点,求它们的公共弦![]() 所在直线的方程.
所在直线的方程.
分析:首先求![]() 、
、![]() 两点的坐标,再用两点式求直线
两点的坐标,再用两点式求直线![]() 的方程,但是求两圆交点坐标的过程太繁.为了避免求交点,可以采用“设而不求”的技巧.
的方程,但是求两圆交点坐标的过程太繁.为了避免求交点,可以采用“设而不求”的技巧.
解:设两圆![]() 、
、![]() 的任一交点坐标为
的任一交点坐标为![]() ,则有:
,则有:
![]() ①
①
![]() ②
②
①-②得:![]() .
.
∵![]() 、
、![]() 的坐标满足方程
的坐标满足方程![]() .
.
∴方程![]() 是过
是过![]() 、
、![]() 两点的直线方程.
两点的直线方程.
又过![]() 、
、![]() 两点的直线是唯一的.
两点的直线是唯一的.
∴两圆![]() 、
、![]() 的公共弦
的公共弦![]() 所在直线的方程为
所在直线的方程为![]() .
.
说明:上述解法中,巧妙地避开了求![]() 、
、![]() 两点的坐标,虽然设出了它们的坐标,但并没有去求它,而是利用曲线与方程的概念达到了目标.从解题的角度上说,这是一种“设而不求”的技巧,从知识内容的角度上说,还体现了对曲线与方程的关系的深刻理解以及对直线方程是一次方程的本质认识.它的应用很广泛.
两点的坐标,虽然设出了它们的坐标,但并没有去求它,而是利用曲线与方程的概念达到了目标.从解题的角度上说,这是一种“设而不求”的技巧,从知识内容的角度上说,还体现了对曲线与方程的关系的深刻理解以及对直线方程是一次方程的本质认识.它的应用很广泛.
典型例题十四
例14 已知对于圆![]() 上任意一点
上任意一点![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
解:运用圆的参数方程,设![]() 的坐标为
的坐标为![]() ,
, ![]()
即![]() ,
,![]() ,
,
∵![]() 恒成立
恒成立
∴![]() 恒成立
恒成立
即![]() 恒成立
恒成立
∴只需![]() 大于等于
大于等于![]() 的最大值.
的最大值.
令![]()
![]() 的最大值为
的最大值为![]()
∴![]()
说明:在上述解法中我们运用了圆上点的参数设法.采用这种设法的优点在于,一方面可以减少参数的个数,另一方面可以灵活地运用三角公式.从代数的观点看,这种设法的实质就是三角代换.
另外本题也可以不用圆的参数方程求解,本题的实质就是求最值问题,方法较多.但以上述解法较简.
典型例题十五
例15 试求圆![]() (
(![]() 为参数)上的点到点
为参数)上的点到点![]() 距离的最大(小)值.
距离的最大(小)值.
分析:利用两点间距离公式求解或数形结合求解.
解法一:设![]() 是圆
是圆![]() 上任一点,则
上任一点,则![]() .所以
.所以
![]()
![]()
![]() .
.
因为![]() ,所以
,所以![]() ,因此
,因此
当![]() 时,
时,![]() .
.
当![]() 时,
时,![]() .
.
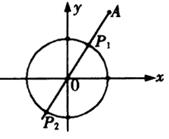
解法二:将圆![]() 代入普通方程得
代入普通方程得![]() .
.
如图所示可得,![]() 、
、![]() 分别是圆上的点到
分别是圆上的点到![]() 的距离的最小值和最大值.易知:
的距离的最小值和最大值.易知:![]() ,
,![]() .
.
说明:
(1)在圆的参数方程![]() (
(![]() 为参数)中,
为参数)中,![]() 为圆心,
为圆心,![]() 为半径,参数
为半径,参数![]() 的几何意义是:圆的半径从
的几何意义是:圆的半径从![]() 轴正向绕圆心按逆时针方向旋转到
轴正向绕圆心按逆时针方向旋转到![]() 所得圆心角的大小.若原点为圆心,常常用
所得圆心角的大小.若原点为圆心,常常用![]() 来表示半径为
来表示半径为![]() 的圆上的任一点.
的圆上的任一点.
(2)圆的参数方程也是解决某些代数问题的一个重要工具.
典型例题十六
例16 已知圆的方程为![]() ,圆内有定点
,圆内有定点![]() ,圆周上有两个动点
,圆周上有两个动点![]() 、
、![]() ,使
,使![]() ,求矩形
,求矩形![]() 的顶点
的顶点![]() 的轨迹方程.
的轨迹方程.
分析:利用几何法求解,或利用转移法求解,或利用参数法求解.
解法一:如图,在矩形![]() 中,连结
中,连结![]() ,
,![]() 交于
交于![]() ,显然
,显然![]() ,
,![]() ,
,
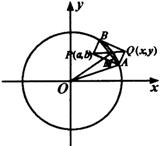
在直角三角形![]() 中,若设
中,若设![]() ,则
,则![]() .
.
由![]() ,即
,即
![]() ,
,
也即![]() ,这便是
,这便是![]() 的轨迹方程.
的轨迹方程.
解法二:设![]() 、
、![]() 、
、![]() ,则
,则![]() ,
,![]() .
.
又![]() ,即
,即
![]() .①
.①
又![]() 与
与![]() 的中点重合,故
的中点重合,故![]() ,
,![]() ,即
,即
![]() ②
②
①+②,有![]() .
.
这就是所求的轨迹方程.
解法三:设![]() 、
、![]() 、
、![]() ,
,
由于![]() 为矩形,故
为矩形,故![]() 与
与![]() 的中点重合,即有
的中点重合,即有
![]() , ①
, ①
![]() , ②
, ②
又由![]() 有
有![]() ③
③
联立①、②、③消去![]() 、
、![]() ,即可得
,即可得![]() 点的轨迹方程为
点的轨迹方程为![]() .
.
说明:本题的条件较多且较隐含,解题时,思路应清晰,且应充分利用图形的几何性质,否则,将使解题陷入困境之中.
本题给出三种解法.其中的解法一是几何方法,它充分利用了图形中隐含的数量关系.而解法二与解法三,从本质上是一样的,都可以称为参数方法.解法二涉及到了![]() 、
、![]() 、
、![]() 、
、![]() 四个参数,故需列出五个方程;而解法三中,由于借助了圆
四个参数,故需列出五个方程;而解法三中,由于借助了圆![]() 的参数方程,只涉及到两个参数
的参数方程,只涉及到两个参数![]() 、
、![]() ,故只需列出三个方程便可.上述三种解法的共同之处是,利用了图形的几何特征,借助数形结合的思想方法求解.
,故只需列出三个方程便可.上述三种解法的共同之处是,利用了图形的几何特征,借助数形结合的思想方法求解.
典型例题十七
例17 设点![]() 是圆
是圆![]() 是任一点,求
是任一点,求![]() 的取值范围.
的取值范围.
分析一:利用圆上任一点的参数坐标代替![]() 、
、![]() ,转化为三角问题来解决.
,转化为三角问题来解决.
解法一:设圆![]() 上任一点
上任一点![]()
则有![]() ,
,![]()
![]()
∴![]() ,∴
,∴![]()
∴![]() .
.
即![]() (
(![]() )
)
∴![]() .
.
又∵![]()
∴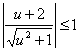
解之得:![]() .
.
分析二:![]() 的几何意义是过圆
的几何意义是过圆![]() 上一动点和定点
上一动点和定点![]() 的连线的斜率,利用此直线与圆
的连线的斜率,利用此直线与圆![]() 有公共点,可确定出
有公共点,可确定出![]() 的取值范围.
的取值范围.
解法二:由![]() 得:
得:![]() ,此直线与圆
,此直线与圆![]() 有公共点,故点
有公共点,故点![]() 到直线的距离
到直线的距离![]() .
.
∴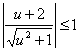
解得:![]() .
.
另外,直线![]() 与圆
与圆![]() 的公共点还可以这样来处理:
的公共点还可以这样来处理:
由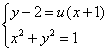 消去
消去![]() 后得:
后得:![]() ,
,
此方程有实根,故![]() ,
,
解之得:![]() .
.
说明:这里将圆上的点用它的参数式表示出来,从而将求变量![]() 的范围问题转化成三角函数的有关知识来求解.或者是利用其几何意义转化成斜率来求解,使问题变得简捷方便.
的范围问题转化成三角函数的有关知识来求解.或者是利用其几何意义转化成斜率来求解,使问题变得简捷方便.
典型例题十八
例18 已知对于圆![]() 上任一点
上任一点![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
分析一:为了使不等式![]() 恒成立,即使
恒成立,即使![]() 恒成立,只须使
恒成立,只须使![]() 就行了.因此只要求出
就行了.因此只要求出![]() 的最小值,
的最小值,![]() 的范围就可求得.
的范围就可求得.
解法一:令![]() ,
,
由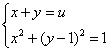
得:![]()
∵![]() 且
且![]() ,
,
∴![]() .
.
即![]() ,∴
,∴![]() ,
,
∴![]() ,即
,即![]()
又![]() 恒成立即
恒成立即![]() 恒成立.
恒成立.
∴![]() 成立,
成立,
∴![]() .
.
分析二:设圆上一点![]() [因为这时
[因为这时![]() 点坐标满足方程
点坐标满足方程![]() ]问题转化为利用三解问题来解.
]问题转化为利用三解问题来解.
解法二:设圆![]() 上任一点
上任一点![]()
![]()
∴![]() ,
,![]()
∵![]() 恒成立
恒成立
∴![]()
即![]() 恒成立.
恒成立.
∴只须![]() 不小于
不小于![]() 的最大值.
的最大值.
设![]()
∴![]() 即
即![]() .
.
说明:在这种解法中,运用了圆上的点的参数设法.一般地,把圆![]() 上的点设为
上的点设为![]() (
(![]() ).采用这种设法一方面可减少参数的个数,另一方面可以灵活地运用三角公式.从代数观点来看,这种做法的实质就是三角代换.
).采用这种设法一方面可减少参数的个数,另一方面可以灵活地运用三角公式.从代数观点来看,这种做法的实质就是三角代换.
典型例题十九
例19 (1)已知圆![]() ,
,![]() 为圆
为圆![]() 上的动点,求
上的动点,求![]() 的最大、最小值.
的最大、最小值.
(2)已知圆![]() ,
,![]() 为圆上任一点.求
为圆上任一点.求![]() 的最大、最小值,求
的最大、最小值,求![]() 的最大、最小值.
的最大、最小值.
分析:(1)、(2)两小题都涉及到圆上点的坐标,可考虑用圆的参数方程或数形结合解决.
解:(1)(法1)由圆的标准方程![]() .
.
可设圆的参数方程为![]() (
(![]() 是参数).
是参数).
则![]()
![]() (其中
(其中![]() ).
).
所以![]() ,
,![]() .
.
(法2)圆上点到原点距离的最大值![]() 等于圆心到原点的距离
等于圆心到原点的距离![]() 加上半径1,圆上点到原点距离的最小值
加上半径1,圆上点到原点距离的最小值![]() 等于圆心到原点的距离
等于圆心到原点的距离![]() 减去半径1.
减去半径1.
所以![]() .
.
![]() .
.
所以![]() .
.![]() .
.
(2) (法1)由![]() 得圆的参数方程:
得圆的参数方程:![]()
![]() 是参数.
是参数.
则![]() .令
.令![]() ,
,
得![]() ,
,![]()
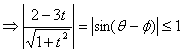
![]() .
.
所以![]() ,
,![]() .
.
即![]() 的最大值为
的最大值为![]() ,最小值为
,最小值为![]() .
.
此时![]() .
.
所以![]() 的最大值为
的最大值为![]() ,最小值为
,最小值为![]() .
.
(法2)设![]() ,则
,则![]() .由于
.由于![]() 是圆上点,当直线与圆有交点时,如图所示,
是圆上点,当直线与圆有交点时,如图所示,
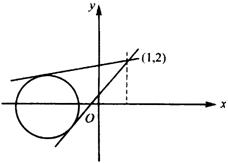
两条切线的斜率分别是最大、最小值.
由![]() ,得
,得![]() .
.
所以![]() 的最大值为
的最大值为![]() ,最小值为
,最小值为![]() .
.
令![]() ,同理两条切线在
,同理两条切线在![]() 轴上的截距分别是最大、最小值.
轴上的截距分别是最大、最小值.
由![]() ,得
,得![]() .
.
所以![]() 的最大值为
的最大值为![]() ,最小值为
,最小值为![]() .
.
典型例题二十
例20 有一种大型商品,![]() 、
、![]() 两地都有出售,且价格相同.某地居民从两地之一购得商品后运回的费用是:每单位距离
两地都有出售,且价格相同.某地居民从两地之一购得商品后运回的费用是:每单位距离![]() 地的运费是
地的运费是![]() 地的运费的3倍.已知
地的运费的3倍.已知![]() 、
、![]() 两地距离为10公里,顾客选择
两地距离为10公里,顾客选择![]() 地或
地或![]() 地购买这种商品的标准是:包括运费和价格的总费用较低.求
地购买这种商品的标准是:包括运费和价格的总费用较低.求![]() 、
、![]() 两地的售货区域的分界线的曲线形状,并指出曲线上、曲线内、曲线外的居民应如何选择购货地点.
两地的售货区域的分界线的曲线形状,并指出曲线上、曲线内、曲线外的居民应如何选择购货地点.
分析:该题不论是问题的背景或生活实际的贴近程度上都具有深刻的实际意义和较强的应用意识,启示我们在学习中要注意联系实际,要重视数学在生产、生活以及相关学科的应用.解题时要明确题意,掌握建立数学模型的方法.
解:以![]() 、
、![]() 所确定的直线为
所确定的直线为![]() 轴,
轴,![]() 的中点
的中点![]() 为坐标原点,建立如图所示的平面直角坐标系.
为坐标原点,建立如图所示的平面直角坐标系.
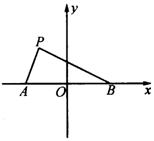
∵![]() ,∴
,∴![]() ,
,![]() .
.
设某地![]() 的坐标为
的坐标为![]() ,且
,且![]() 地居民选择
地居民选择![]() 地购买商品便宜,并设
地购买商品便宜,并设![]() 地的运费为
地的运费为![]() 元/公里,
元/公里,![]() 地的运费为
地的运费为![]() 元/公里.因为
元/公里.因为![]() 地居民购货总费用满足条件:
地居民购货总费用满足条件:
价格+![]() 地运费≤价格+
地运费≤价格+![]() 地的运费
地的运费
即:![]() .
.
∵![]() ,
,
∴![]()
化简整理得:![]()
∴以点![]() 为圆心
为圆心![]() 为半径的圆是两地购货的分界线.
为半径的圆是两地购货的分界线.
圆内的居民从![]() 地购货便宜,圆外的居民从
地购货便宜,圆外的居民从![]() 地购货便宜,圆上的居民从
地购货便宜,圆上的居民从![]() 、
、![]() 两地购货的总费用相等.因此可随意从
两地购货的总费用相等.因此可随意从![]() 、
、![]() 两地之一购货.
两地之一购货.
说明:实际应用题要明确题意,建议数学模型.