(数学选修1-1)第二章 圆锥曲线[提高训练C组]及答案
一、选择题
1.若抛物线![]() 上一点
上一点![]() 到准线的距离等于它到顶点的距离,则点
到准线的距离等于它到顶点的距离,则点![]() 的坐标为( )
的坐标为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.椭圆![]() 上一点
上一点![]() 与椭圆的两个焦点
与椭圆的两个焦点![]() 、
、![]() 的连线互相垂直,
的连线互相垂直,
则△![]() 的面积为(
)
的面积为(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.若点![]() 的坐标为
的坐标为![]() ,
,![]() 是抛物线
是抛物线![]() 的焦点,点
的焦点,点![]() 在
在
抛物线上移动时,使![]() 取得最小值的
取得最小值的![]() 的坐标为( )
的坐标为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.与椭圆![]() 共焦点且过点
共焦点且过点![]() 的双曲线方程是( )
的双曲线方程是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.若直线![]() 与双曲线
与双曲线![]() 的右支交于不同的两点,
的右支交于不同的两点,
那么![]() 的取值范围是( )
的取值范围是( )
A.(![]() ) B.(
) B.(![]() ) C.(
) C.(![]() ) D.(
) D.(![]() )
)
6.抛物线![]() 上两点
上两点![]() 、
、![]() 关于直线
关于直线![]() 对称,
对称,
且![]() ,则
,则![]() 等于( )
等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题
1.椭圆![]() 的焦点
的焦点![]() 、
、![]() ,点
,点![]() 为其上的动点,当∠
为其上的动点,当∠![]()
![]()
![]() 为钝角时,点
为钝角时,点![]() 横坐标的取值范围是
。
横坐标的取值范围是
。
2.双曲线![]() 的一条渐近线与直线
的一条渐近线与直线![]() 垂直,则这双曲线的离心率为___。
垂直,则这双曲线的离心率为___。
3.若直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 、
、![]() 两点,若线段
两点,若线段![]() 的中点的横坐标是
的中点的横坐标是![]() ,则
,则![]() ______。
______。
4.若直线![]() 与双曲线
与双曲线![]() 始终有公共点,则
始终有公共点,则![]() 取值范围是
。
取值范围是
。
5.已知![]() ,抛物线
,抛物线![]() 上的点到直线
上的点到直线![]() 的最段距离为__________。
的最段距离为__________。
三、解答题
1.当![]() 变化时,曲线
变化时,曲线![]() 怎样变化?
怎样变化?
2.设![]() 是双曲线
是双曲线![]() 的两个焦点,点
的两个焦点,点![]() 在双曲线上,且
在双曲线上,且![]() ,
,
求△![]() 的面积。
的面积。
3.已知椭圆![]() ,
,![]() 、
、![]() 是椭圆上的两点,线段
是椭圆上的两点,线段![]() 的垂直
的垂直
平分线与![]() 轴相交于点
轴相交于点![]() .证明:
.证明:![]()
4.已知椭圆![]() ,试确定
,试确定![]() 的值,使得在此椭圆上存在不同
的值,使得在此椭圆上存在不同
两点关于直线![]() 对称。
对称。
(数学选修1-1) 第二章 圆锥曲线 [提高训练C组]
一、选择题
1.B 点![]() 到准线的距离即点
到准线的距离即点![]() 到焦点的距离,得
到焦点的距离,得![]() ,过点
,过点![]() 所作的高也是中线
所作的高也是中线
![]() ,代入到
,代入到![]() 得
得![]() ,
,![]()
2.D ![]() ,相减得
,相减得
![]()
3.D ![]() 可以看做是点
可以看做是点![]() 到准线的距离,当点
到准线的距离,当点![]() 运动到和点
运动到和点![]() 一样高时,
一样高时,![]() 取得最小值,即
取得最小值,即![]() ,代入
,代入![]() 得
得![]()
4.A ![]() 且焦点在
且焦点在![]() 轴上,可设双曲线方程为
轴上,可设双曲线方程为![]() 过点
过点![]()
得![]()
5.D  有两个不同的正根
有两个不同的正根
则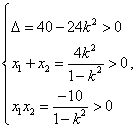 得
得![]()
6.A ![]() ,且
,且![]()
在直线![]() 上,即
上,即![]()
![]()
二、填空题
1.![]() 可以证明
可以证明![]() 且
且![]()
而![]() ,则
,则![]()
![]() 即
即![]()
2.![]() 渐近线为
渐近线为![]() ,其中一条与与直线
,其中一条与与直线![]() 垂直,得
垂直,得![]()
![]()
3.![]()
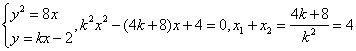
得![]() ,当
,当![]() 时,
时,![]() 有两个相等的实数根,不合题意
有两个相等的实数根,不合题意
当![]() 时,
时,![]()
4.![]()
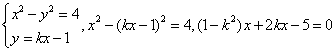
当![]() 时,显然符合条件;
时,显然符合条件;
当![]() 时,则
时,则![]()
5.![]() 直线
直线![]() 为
为![]() ,设抛物线
,设抛物线![]() 上的点
上的点![]()
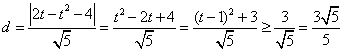
三、解答题
1.解:当![]() 时,
时,![]() ,曲线
,曲线![]() 为一个单位圆;
为一个单位圆;
当![]() 时,
时,![]() ,曲线
,曲线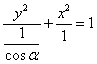 为焦点在
为焦点在![]() 轴上的椭圆;
轴上的椭圆;
当![]() 时,
时,![]() ,曲线
,曲线![]() 为两条平行的垂直于
为两条平行的垂直于![]() 轴的直线;
轴的直线;
当![]() 时,
时,![]() ,曲线
,曲线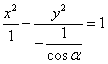 为焦点在
为焦点在![]() 轴上的双曲线;
轴上的双曲线;
当![]() 时,
时,![]() ,曲线
,曲线![]() 为焦点在
为焦点在![]() 轴上的等轴双曲线。
轴上的等轴双曲线。
2.解:双曲线![]() 的
的![]() 不妨设
不妨设![]() ,则
,则![]()
![]() ,而
,而![]()
得![]()
![]()
3.证明:设![]() ,则中点
,则中点![]() ,得
,得![]()
![]()
![]() 得
得![]()
即![]() ,
,![]() 的垂直平分线的斜率
的垂直平分线的斜率![]()
![]() 的垂直平分线方程为
的垂直平分线方程为![]()
当![]() 时,
时,![]()
而![]() ,
,![]()
4.解:设![]() ,
,![]() 的中点
的中点![]() ,
,![]()
而![]()
![]() 相减得
相减得![]()
即![]() ,
,![]()
而![]() 在椭圆内部,则
在椭圆内部,则![]() 即
即![]() 。
。