(数学选修1-1)第二章 圆锥曲线 [综合训练B组]及答案
一、选择题
1.如果![]() 表示焦点在
表示焦点在![]() 轴上的椭圆,那么实数
轴上的椭圆,那么实数![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.以椭圆![]() 的顶点为顶点,离心率为
的顶点为顶点,离心率为![]() 的双曲线方程( )
的双曲线方程( )
A.![]() B.
B.![]()
C.![]() 或
或![]() D.以上都不对
D.以上都不对
3.过双曲线的一个焦点![]() 作垂直于实轴的弦
作垂直于实轴的弦![]() ,
,![]() 是另一焦点,若∠
是另一焦点,若∠![]() ,
,
则双曲线的离心率![]() 等于( )
等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.![]() 是椭圆
是椭圆![]() 的两个焦点,
的两个焦点,![]() 为椭圆上一点,且∠
为椭圆上一点,且∠![]() ,则
,则
Δ![]() 的面积为(
)
的面积为(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.以坐标轴为对称轴,以原点为顶点且过圆![]() 的圆心的抛物线的方程是( )
的圆心的抛物线的方程是( )
A.![]() 或
或![]() B.
B.![]()
C.![]() 或
或![]() D.
D.![]() 或
或![]()
6.设![]() 为过抛物线
为过抛物线![]() 的焦点的弦,则
的焦点的弦,则![]() 的最小值为( )
的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.无法确定
D.无法确定
二、填空题
1.椭圆![]() 的离心率为
的离心率为![]() ,则
,则![]() 的值为______________。
的值为______________。
2.双曲线![]() 的一个焦点为
的一个焦点为![]() ,则
,则![]() 的值为______________。
的值为______________。
3.若直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 、
、![]() 两点,则线段
两点,则线段![]() 的中点坐标是______。
的中点坐标是______。
4.对于抛物线![]() 上任意一点
上任意一点![]() ,点
,点![]() 都满足
都满足![]() ,则
,则![]() 的取值范围是____。
的取值范围是____。
5.若双曲线![]() 的渐近线方程为
的渐近线方程为![]() ,则双曲线的焦点坐标是_________.
,则双曲线的焦点坐标是_________.
6.设![]() 是椭圆
是椭圆![]() 的不垂直于对称轴的弦,
的不垂直于对称轴的弦,![]() 为
为![]() 的中点,
的中点,![]() 为坐标原点,
为坐标原点,
则![]() ____________。
____________。
三、解答题
1.已知定点![]() ,
,![]() 是椭圆
是椭圆![]() 的右焦点,在椭圆上求一点
的右焦点,在椭圆上求一点![]() ,
,
使![]() 取得最小值。
取得最小值。
2.![]() 代表实数,讨论方程
代表实数,讨论方程![]() 所表示的曲线
所表示的曲线
3.双曲线与椭圆![]() 有相同焦点,且经过点
有相同焦点,且经过点![]() ,求其方程。
,求其方程。
4. 已知顶点在原点,焦点在![]() 轴上的抛物线被直线
轴上的抛物线被直线![]() 截得的弦长为
截得的弦长为![]() ,
,
求抛物线的方程。
(数学选修1-1) 第二章 圆锥曲线 [综合训练B组]
一、选择题
1.D 焦点在![]() 轴上,则
轴上,则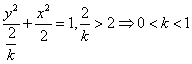
2.C 当顶点为![]() 时,
时,![]() ;
;
当顶点为![]() 时,
时,![]()
3.C Δ![]() 是等腰直角三角形,
是等腰直角三角形,![]()
![]()
4.C ![]()
![]()
![]()
![]()
5.D 圆心为![]() ,设
,设![]() ;
;
设![]()
6.C 垂直于对称轴的通径时最短,即当![]()
![]()
二、填空题
1.![]() 当
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]()
2.![]() 焦点在
焦点在![]() 轴上,则
轴上,则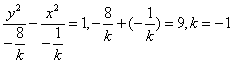
3.![]()
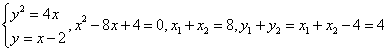
中点坐标为![]()
4.![]() 设
设![]() ,由
,由![]() 得
得![]()
![]() 恒成立,则
恒成立,则![]()
5. ![]() 渐近线方程为
渐近线方程为![]() ,得
,得![]() ,且焦点在
,且焦点在![]() 轴上
轴上
6. ![]() 设
设![]() ,则中点
,则中点![]() ,得
,得![]()
![]() ,
,![]() ,
,![]()
![]() 得
得![]() 即
即![]()
三、解答题
1.解:显然椭圆![]() 的
的![]() ,记点
,记点![]() 到右准线的距离为
到右准线的距离为![]()
则![]() ,即
,即![]()
当![]() 同时在垂直于右准线的一条直线上时,
同时在垂直于右准线的一条直线上时,![]() 取得最小值,
取得最小值,
此时![]() ,代入到
,代入到![]() 得
得![]()
而点![]() 在第一象限,
在第一象限,![]()
2.解:当![]() 时,曲线
时,曲线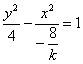 为焦点在
为焦点在![]() 轴的双曲线;
轴的双曲线;
当![]() 时,曲线
时,曲线![]() 为两条平行的垂直于
为两条平行的垂直于![]() 轴的直线;
轴的直线;
当![]() 时,曲线
时,曲线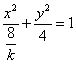 为焦点在
为焦点在![]() 轴的椭圆;
轴的椭圆;
当![]() 时,曲线
时,曲线![]() 为一个圆;
为一个圆;
当![]() 时,曲线
时,曲线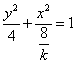 为焦点在
为焦点在![]() 轴的椭圆。
轴的椭圆。
3.解:椭圆![]() 的焦点为
的焦点为![]() ,设双曲线方程为
,设双曲线方程为![]()
过点![]() ,则
,则![]() ,得
,得![]() ,而
,而![]() ,
,
![]() ,双曲线方程为
,双曲线方程为![]() 。
。
4.解:设抛物线的方程为![]() ,则
,则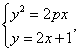 消去
消去![]() 得
得
![]()
![]()
![]() ,
,
则![]()
![]()