高二数学第一学期期末调查测试
数 学 试 题 2008.1
一、填空题(本小题共14小题,每小题5分,共70分,只要求写出结果,不必写出计算和推理过程)
1.双曲线![]() 的一个焦点坐标为
。
的一个焦点坐标为
。
2.“![]() 函数
函数![]() 满足
满足![]() ”的否定是
。
”的否定是
。
3.某商场有四类食品,其中粮食类,植物油类,动物性食品及果蔬类分别有40种,10种,30种,20种,现从中抽取一个容量为20的样本进行食品安全检测。若采用分层抽样的方法抽取样本,则抽取的植物油类与果蔬类食品种数之和
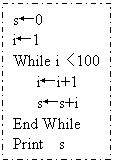 4.在等腰直角三角形ABC的斜边AB上任取一点M,AM小于AC的概率为
4.在等腰直角三角形ABC的斜边AB上任取一点M,AM小于AC的概率为
5.从一条生产线上每隔30分钟取一件产品,共取了n件,测得它们的长度(cm)后,画出其频率分布直方图,若长度在![]() 单位(cm)
单位(cm)
内频数为40,则长度为![]() 单位(cm)内产品频数是
单位(cm)内产品频数是
6.试写出三个实数a,b,c成等比数列的一个充要条件
7.阅读本题的伪代码,其输出结果应为
8.点P是抛物线![]() 上一动点,则点P到点(0,-1)的距离与抛物线准线的距离之和的最小值是
上一动点,则点P到点(0,-1)的距离与抛物线准线的距离之和的最小值是
9.已知变量x与变量y之间的一组数据如上表,则y与x的线性回归直线![]() 必过点
必过点
![]()
10.如果直线L是曲线![]() 在点
在点![]() 的切线,则切线L的方程
的切线,则切线L的方程
11.以椭圆的右焦点![]() 为圆心的圆恰好过椭圆的中心,交椭圆于点M,N,椭圆的左焦点为
为圆心的圆恰好过椭圆的中心,交椭圆于点M,N,椭圆的左焦点为![]() ,且直线
,且直线![]() 与此圆相切,则椭圆的离心率e为
与此圆相切,则椭圆的离心率e为
12.过抛物线焦点F的直线与抛物线相交于P,Q两点,若P,Q在抛物线的准线上的射影于![]() ,则
,则![]() 等于
等于
13.半径为r的圆的面积![]() ,周长
,周长![]() ,若将r看作
,若将r看作![]() 上的变量,则
上的变量,则![]() ①. ①式可以用语言叙述为:圆的面积函数的导数等于圆的周长函数.对于半径为R的球,若将R看作
①. ①式可以用语言叙述为:圆的面积函数的导数等于圆的周长函数.对于半径为R的球,若将R看作![]() 上的变量,请你写出类似于①的式子
②,②式可以用语言叙述为:
上的变量,请你写出类似于①的式子
②,②式可以用语言叙述为:
14.给出下列四个命题:
①![]() ②
② ![]() ③(sinx)’=cosx ④(cosx)’= sinx
③(sinx)’=cosx ④(cosx)’= sinx
其中真命题的序号为
二.解答题(本大题共6小题,共90分,解答应写出文字说明、证明过程或演算步骤)
15(本小题满分14分)将一颗骰子先后抛掷两次,观察向上的点数,依次为x,y,构成一个数对(x,y),问:
(1)不同数对共有 个;
(2)两数之和为5的倍数的概率是多少?
(3)两数至少有一个是5或6的概率?
16.(本小题满分14分)已知命题P:方程![]() 所表示的曲线为焦点在x轴上的椭圆;
所表示的曲线为焦点在x轴上的椭圆;
命题q:关于实数t的不等式![]()
(1) 若命题P为真,求实数t的取值范围;
(2) 若命题P是命题q的充分不必要条件,求实数a的取值范围。
17(本小题15分)甲,乙两人在相同条件下各射靶10次,进行射击水平测试,每次命中的环数分别是:
甲:8 7 8 6 5 9 10 4 7
乙:7 7 8 6 7 8 7 9 5
(1) 分别计算以上两组数据的平均数;
(2) 分别求出两组数据的方差;
(3) 根据计算结果估计一下两人的射击情况,如果要选拔一人参加比赛,你认为应选拔那位比较合适?
18.(本小题满分15分)已知![]()
(1)求![]() 的单调递增区间和单调递减区间;
的单调递增区间和单调递减区间;
(2)若当![]() 时,
时,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)试讨论关于x的方程![]() 的解的个数。
的解的个数。
19.(本小题满分16分)已知![]() 、
、![]() 分别为椭圆C:
分别为椭圆C:![]() 的左右两焦点,点A为椭圆的左顶点,且椭圆C上的点B
的左右两焦点,点A为椭圆的左顶点,且椭圆C上的点B![]() 到
到![]() 、
、![]() 两点的距离之和为4。
两点的距离之和为4。
(1)求椭圆C的方程;
(2)过椭圆C的焦点![]() 作平行线交椭圆C于P,Q两点,求
作平行线交椭圆C于P,Q两点,求![]() 的面积。
的面积。
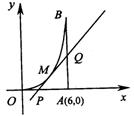
20.(本小题满分16分)、如图所示,曲线段![]() 是函数
是函数![]() 的图象,BA⊥x轴于A,曲线段
的图象,BA⊥x轴于A,曲线段![]() 上一点
上一点![]() 处的切线
处的切线![]() 交x轴于
交x轴于![]() ,交线段
,交线段![]() 于
于![]() .
.
(1)试用![]() 表示切线PQ的方程;
表示切线PQ的方程;
(2)设![]() 的面积为
的面积为![]() ,若函数
,若函数![]() 在
在![]() 上单调递减,试求出
上单调递减,试求出![]() 的最小值;
的最小值;
|
淮安市2007-2008学年度高二第一学期期调查测试数学试题参考答案及评分标准
一,填空题(本大题共14题,每小题5分,共70分)
(1)
填(5,0),(-5,0);(2)![]() ,函数
,函数![]() 满足
满足![]()
(3)6; (4)![]() ; (5)16;(6)
; (5)16;(6)![]()
(7)5049;(8)![]() ;(9)(1.5,4);(10)
;(9)(1.5,4);(10)![]()
(11)![]() ;(12)900;(13)
;(12)900;(13)![]() ,球的体积函数的导数等于球的表面积函数;(14)(2)、(3)
,球的体积函数的导数等于球的表面积函数;(14)(2)、(3)
二、解答题(本大题共6题,共90分)
15.(本小题满分14分)
(1)36----------------3分
(2)两数之和是5的倍数包含以下基本事件:
(1,4)(4,1)(2,3)(4,6)(6,4)(5,5)共7个,所以,两数之和是5的倍数的概率是![]() ----------------8分
----------------8分
(3)此事件的对立事件是两数都不是5或6,其基本事件有![]() 个,所以,两数中至少有一个是5或6的概率是
个,所以,两数中至少有一个是5或6的概率是![]() --------14分
--------14分
16.(本小题满分14分)
(1)![]() 方程
方程![]() 所表示的曲线为焦点在
所表示的曲线为焦点在![]() 轴上的椭圆
轴上的椭圆
![]()
![]() ------------4分
------------4分
解得:![]() ------------7分
------------7分
(2)![]() 命题P是命题q的充分不必要条件
命题P是命题q的充分不必要条件
![]()
![]() 是不等式
是不等式![]() 解集的真子集-------10分
解集的真子集-------10分
法一:因方程![]() 两根为
两根为![]() 故只需
故只需![]() -----12分
-----12分
解得:![]() ----------14分
----------14分
法二:令![]() ,因
,因![]() ------12分
------12分
解得:![]() -------------14分
-------------14分
17(本小题满分15分)
(1)![]()
![]() -----------4分
-----------4分
(2)![]() -------8分
-------8分
![]() --------12分
--------12分
(3)![]() ,故乙较甲稳定,应该选乙 ---------15分
,故乙较甲稳定,应该选乙 ---------15分
18:(本小题满分15分)
(1)![]() ------2分
------2分
由![]()
![]()
![]() 的单调递增区间
的单调递增区间![]() --------4分
--------4分
![]()
![]()
![]() 的单调递减区间
的单调递减区间![]() --------5分
--------5分
(2)由(1)知,函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减
上单调递减
-------------------------------------------------------------------------------------7分
又![]()
![]() 实数a的取值范围为
实数a的取值范围为![]() -----------10分
-----------10分
(3)由(1)知函数![]() 的极大值为
的极大值为![]() ,极小值
,极小值![]() 分
分
所以当![]() 时,方程
时,方程![]() =b有一解;当
=b有一解;当![]() 方程
方程![]() =b有两解;
=b有两解;![]() 方程
方程![]() =b有三解-------------------------------------------------15分
=b有三解-------------------------------------------------15分
19:(本小题满分16分)
(1)
由定义知![]() ----------2分
----------2分
又点B![]() 在椭圆
在椭圆![]() 上,所以有
上,所以有
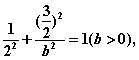 解得
解得![]() ---------------------4分
---------------------4分
所以椭圆C的的方程![]() --------------6分
--------------6分
(2) 由(1)知焦点的坐标为(1,0)
又过![]() 的直线PQ平行AB,A为椭圆的左顶点,所以PQ所在直线方程为
的直线PQ平行AB,A为椭圆的左顶点,所以PQ所在直线方程为![]() ----------------------10分
----------------------10分
设![]()
将![]() 代入椭圆方程得:
代入椭圆方程得:![]() 解得:
解得:![]() ,-------12分
,-------12分
故![]() --------14分
--------14分
所以![]() 的面积
的面积![]() ------16分
------16分
(其它解法,酌情给分)
20(本小题满分16分)
(1)![]() ,
,![]() ------2分
------2分
所以直线PQ方程为:![]()
即![]() ------4分
------4分
(2)令![]() 中
中![]() 得
得![]() ,再令
,再令![]() 得
得![]()
所以![]()
即![]() ,
,![]() ----6分
----6分
所以![]() -------------------8分
-------------------8分
又![]() 是函数
是函数![]() 减区间
减区间![]() ,
,![]() ----10分
----10分
(3)![]()
当![]() 时,
时,![]() ,
,![]() 为减函数,此时
为减函数,此时![]()
当![]() 时,
时,![]() ,
,![]() 为增函数,此时
为增函数,此时![]()
故当![]() 时,
时,![]() ------12分
------12分
又![]() ,所以方程
,所以方程![]() 的解应在
的解应在
(0,4)内且只有一个,观察得![]() --------14分
--------14分
![]()
![]() 时,
时,![]()
所以点P横坐标![]() ----------16分
----------16分