高二数学第二学期第一次月考试卷
(立体几何部分测试)
满分:150分 时间:120分钟 命题人:王 春
一. 选择题(本题共60分,每小题5分)
1.直线a//平面α, 直线b//平面α,那么直线a与b的位置关系是( )
A.平行 B.相交 C.异面 D.都有可能
2.下列说法正确的是( )
A. 正三棱锥是正四面体; B. 长方体是正四棱柱;
C. 平行六面体不可能是直四棱柱 D. 正四棱柱是长方体.
3.已知点E是以点P为顶点的棱锥的某一条侧棱PA上的一个三等分点,PE=2EA,过点E且平行于棱锥底面的截面面积为S1,棱锥的底面面积为S2,则S1:S2= ( )
A. 1:9
B. 4:
4.已知一个简单多面体的各个顶点都有三条棱,面数、顶点数分别为F,V,那么
A. 2 B.
5. 不共面的三条定直线![]() ,
,![]() ,
,![]() 互相平行,点A在
互相平行,点A在![]() 上,点B在
上,点B在![]() 上,C、D两点在
上,C、D两点在![]() 上,若CD
上,若CD![]() (定值),则三棱锥A-BCD的体积( )
(定值),则三棱锥A-BCD的体积( )
A.由A点的变化而变化 B.由B点的变化而变化
C.有最大值,无最小值 D.为定值
6.甲烷分子由一个碳原子和四个氢原子组成,其空间构型为一个各条棱都相等的四面体,四个氢原子分别位于该四面体的四个顶点上,碳原子位于该四面体的中心,它与每个氢原子的距离都是a. 若将碳原子和氢原子均视为一个点,则任意两个氢原子之间的距离( )
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
7. 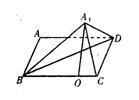 如图,矩形
如图,矩形![]() 中,
中,![]() 沿对角线
沿对角线![]() 将△
将△![]() 折起得到△
折起得到△![]() 且点
且点![]() 在平面
在平面![]() 上的射影
上的射影![]() 落在
落在![]() 边上,记二面角
边上,记二面角![]() 的平面角的大小为
的平面角的大小为![]() ,则
,则![]() 的值等于(
)
的值等于(
)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
8.二面角α—l—β的平面角为600,A、B∈l,AC![]() α,BD
α,BD![]() β,AC⊥l,BD⊥l,若AB=AC=BD=1,则CD的长为 ( )
β,AC⊥l,BD⊥l,若AB=AC=BD=1,则CD的长为 ( )
A.![]() B.
B.![]() C.2 D.
C.2 D.![]()
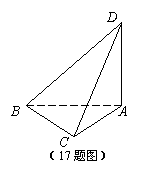 9.把一副三角板ABC与ABD摆成右图所示的直二面角D-AB-C,
9.把一副三角板ABC与ABD摆成右图所示的直二面角D-AB-C,
则异面直线DC与AB所成角的正切值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 不存在
D. 不存在
10.在棱长为1的正方体![]() 的密闭容器中,棱
的密闭容器中,棱

![]() 和棱
和棱![]() 的中点处各有一个小孔,顶点
的中点处各有一个小孔,顶点![]() 处也有一个小
处也有一个小
孔,若正方体可任意放置,且小孔面积不计,则这个正方体容
器中最多可容纳水的体积是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.正四棱锥P-ABCD的斜高等于底面的边长,则相对的两个
侧面PAB与PDC所成二面角的度数是( )
A. ![]() B.
B. ![]() C.
C.
![]() D.
D.
![]()
12.![]() 、
、![]() 、
、![]() 三点在半径为6的球面上,且它们两两之间的球面距离为
三点在半径为6的球面上,且它们两两之间的球面距离为![]() ,则球心
,则球心![]() 到平面
到平面![]() 的距离是( )
的距离是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 二 、填空题(本题共16分,每小题4分)
二 、填空题(本题共16分,每小题4分)
13.一个球的内接正方体与外切正方体的表面积之比是 .
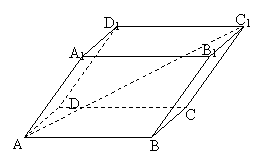
14.如图在平行六面体ABCD—A1B1C1D1中,若AB=4,
AD=3,AA1=5,BAD=900,∠BAA1=∠DAA1=600,
则AC1= 。
15.已知![]() 是边长为
是边长为![]() 的正三角形,那么在空间与这个三角形的三个顶点的距离都等于1的不同平面的个数有
.
的正三角形,那么在空间与这个三角形的三个顶点的距离都等于1的不同平面的个数有
.
16.如图,在正方体ABCD-A1B
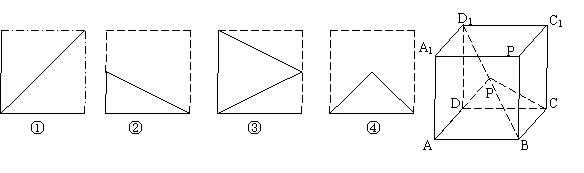 可能是
可能是
![]() 高二数学月考答题试卷
高二数学月考答题试卷
满分:150分 时间:120分钟
| 题号 | 选择题 | 填空题 | 17 | 18 | 19 | 20 | 21 | 22 | 总分 |
| 得分 |
|
一、选择题答题栏(共60分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
二.填空题(本题共16分,每小题4分)
13. . 14. .
15. . 16. .
三、解答题(本题共74分)
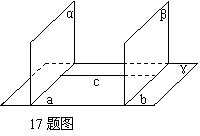
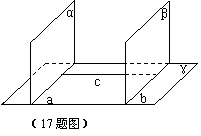 17.(本题12分)如图,已知平面α⊥平面γ,平面β⊥平面γ。α∩γ=a,β∩γ=b且a∥b,求证α∥β。
17.(本题12分)如图,已知平面α⊥平面γ,平面β⊥平面γ。α∩γ=a,β∩γ=b且a∥b,求证α∥β。
18.(本题12分)如图,已知四棱锥![]() 的侧面是正三角形,
的侧面是正三角形, ![]() 是
是![]() 的中点
的中点
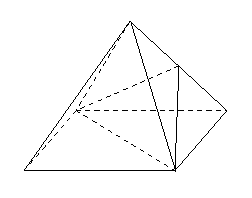
 求证:(1)
求证:(1)![]() ‖
‖![]() (6分)
(6分)
(2) 平面BDE ![]() 平面PAC (6分)
平面PAC (6分)
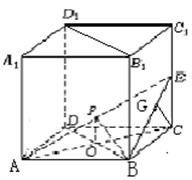
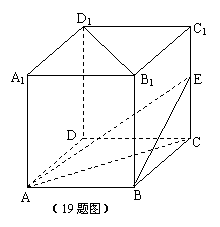 19.(本题12分)在正方体
19.(本题12分)在正方体![]() 中,棱长
中,棱长![]() .
.![]() 为棱
为棱![]() 的中点,
的中点,
(1)求二面角![]() 的大小; ( 6分)
的大小; ( 6分)
(2)求点![]() 到平面
到平面![]() 的距离. ( 6分)
的距离. ( 6分)
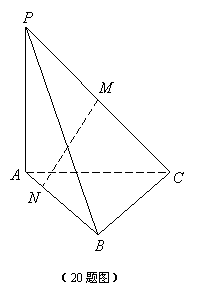 20. (本题12分)已知三棱锥P-ABC的底面为正三角形, PA⊥平面ABC, 点M、N分别在PC、AB上,且PM=MC,BN=3NA.
20. (本题12分)已知三棱锥P-ABC的底面为正三角形, PA⊥平面ABC, 点M、N分别在PC、AB上,且PM=MC,BN=3NA.
(1)求证: MN⊥AB;
(2)若BC=2, 且MN与底面ABC成![]() 角,求三棱锥P-ABC的体积.
角,求三棱锥P-ABC的体积.
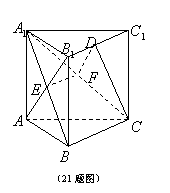
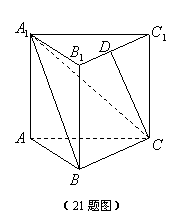 21.(本题12分)在直三棱柱
21.(本题12分)在直三棱柱![]() 中,点
中,点![]() 是
是![]() 的中点,底面三角形
的中点,底面三角形![]() 是直角三角形,
是直角三角形,![]() ,
,![]() ,
,![]() ,
,
(1)求C1到平面A1BC的距离;
(2)求直线![]() 与平面
与平面![]() 所成的角.
所成的角.
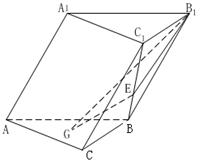
![]() 22. (本题14分) 如图,在斜三棱柱ABC-A1B1C1中,侧面AA1B1B⊥底面ABC,侧棱AA1与底面ABC成600的角, AA1= 2.底面ABC是边长为2的正三角形,其重心为G点。E是线段BC1上一点,且BE=
22. (本题14分) 如图,在斜三棱柱ABC-A1B1C1中,侧面AA1B1B⊥底面ABC,侧棱AA1与底面ABC成600的角, AA1= 2.底面ABC是边长为2的正三角形,其重心为G点。E是线段BC1上一点,且BE=![]() BC1 .
BC1 .
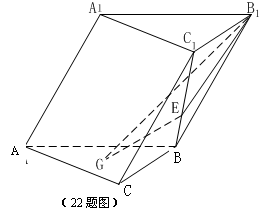 (1)求证:GE∥侧面AA1B1B
;
(1)求证:GE∥侧面AA1B1B
;
(2)求平面B1GE与底面ABC所成锐二
面角的大小
2007---2008学年德一中下学期第一次月考高二数学答案
一.选择题(本题共60分,每小题5分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | D | D | D | B | D | A | B | A | C | C | B | B |
二.填空题(本题共16分,每小题4分)
13. 1:3 . 14. ![]() 15. 5个 16. ①④
15. 5个 16. ①④
 三.解答题(本题共74分)
三.解答题(本题共74分)
17.证明:在平面γ内作直线c⊥a,…
… 2'
∵a∥b,∴c⊥b。 … … 4'
∵α⊥γ,∴c⊥α,
又∵β⊥γ,∴c⊥β,
… … 10'
∴α∥β
… … 12'
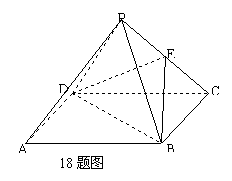 18 证明:(1)连结AC交BD于0点,连结EO
18 证明:(1)连结AC交BD于0点,连结EO
则O为AC的中点,则有OE为中位线∴OE‖AP
∴![]() ‖
‖![]() ………6'
………6'
(2)在△BCP中,有BE⊥PC
在△DCP中,有DE⊥PC又DE∩BE=E故有PC⊥面BDE
又PC在平面PAC上
∴平面BDE ![]() 平面PAC ………12'
平面PAC ………12'
19.解: (1) 连结![]() 与
与![]() 交于
交于![]() 点,则
点,则![]() 面
面![]() ,过点
,过点![]() 作
作![]() 于
于![]() 点,连结
点,连结![]() ,则
,则![]() 即二面角
即二面角![]() 的平面角,
的平面角,
 在
在![]() 中,
中,![]()
![]() ,
,![]()
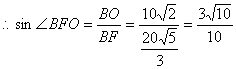 ,
,
![]() . (或
. (或![]() ,
,![]() ) …
… …6'
) …
… …6'
(2) ![]() ∥
∥![]() ,
,![]() 到平面
到平面![]() 的距离即
的距离即![]() 到平面
到平面![]() 的距离,
的距离,
又因为点![]() 是
是![]() 的中点,
的中点,![]() 到平面
到平面![]() 的距离即点
的距离即点![]() 到平面
到平面![]() 的距离,
的距离,![]() 面
面![]() ,
,![]() 面
面![]() 面
面![]() ,
,
过点![]() 作
作![]() 的垂线交于点
的垂线交于点![]() ,则
,则![]() 面
面![]() ,
,
![]() 的长即点
的长即点![]() 到面
到面![]() 的距离,
的距离,
在![]() 中,
中,![]() ,
,
![]() 到平面
到平面![]() 的距离为
的距离为![]() . … … …12'
. … … …12'
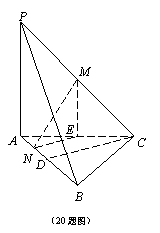 20. 解:(1)取AC的中点E,AB的中点D,连接ME、NE、CD,
20. 解:(1)取AC的中点E,AB的中点D,连接ME、NE、CD,
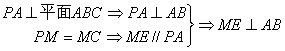
又
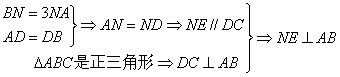
∴ AB⊥平面MNE ∴ AB⊥MN … … …6'
(2)由(1)可知:PA⊥平面ABC,且ME//PA ∴ ME⊥平面ABC
∴
∠MNE=![]() , ∴ ME=NE
, ∴ ME=NE
在正△ABC中,BC=2, 故有 PA=2ME=2NE=DC=![]() ,
,![]()
所以三棱锥P-ABC的体积![]() … … …12'
… … …12'
 21.解:(1)
21.解:(1)![]()
所以C1到平面A1BC的距离等于B1到平面A1BC的距离
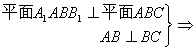
![]()
![]() ,
,
连接![]() 交
交![]() 于
于![]() ,则
,则![]() , 所以 EB1⊥平面A1BC
, 所以 EB1⊥平面A1BC
又
![]() , ∴
, ∴![]() 所以C1到平面A1BC的距离等于
所以C1到平面A1BC的距离等于![]() . ………6'
. ………6'
(2)取![]() 的中点F,连接EF、DF, 则
的中点F,连接EF、DF, 则 ![]() 所以,
所以,![]()
又 EB1⊥平面A1BC 所以 DF⊥平面A1BC ∴ ![]() 即为直线
即为直线![]() 与平面
与平面![]() 所成的角.
所成的角.
且 ![]() ,
,![]() ∴
∴
![]() ,
, ![]() .
.
所以,直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() . … …
…12'
. … …
…12'
22.解法1:(1)延长B1E交BC于F, ∵ΔB1EC∽ΔFEB, BE=![]() EC1
EC1
∴BF=![]() B1C1=
B1C1=![]() BC,从而F为BC的中点. ………………
……………3′
BC,从而F为BC的中点. ………………
……………3′
∵G为ΔABC的重心,
∴A、G、F三点共线,且![]() =
=![]() =
=![]() , ∴GE∥AB1,
, ∴GE∥AB1,
又GE![]() 侧面AA1B1B,
∴GE∥侧面AA1B1B ………………
………7'
侧面AA1B1B,
∴GE∥侧面AA1B1B ………………
………7'
(2)在侧面AA1B1B内,过B1作B1H⊥AB,垂足为H,
∵侧面AA1B1B⊥底面ABC,
∴B1H⊥底面ABC.又侧棱AA1与底面ABC成600的角, AA1= 2,
∴∠B1BH=600,BH=1,B1H=![]() .
.
在底面ABC内,过H作HT⊥AF,垂足为T,连B1T.由三垂线定理有B1T⊥AF,
又平面B1GE与底面ABC的交线为AF,
∴∠B1TH为所求二面角的平面角.……9'
∴AH=AB+BH=3,∠HAT=300,
∴HT=AHsin300=![]() ,
,
在RtΔB1HT中,tan∠B1TH=![]() =
=![]() ,
,
从而平面B1GE与底面ABC所成锐二面角的大小为arctan![]() ……………… 14′
……………… 14′
解法2:(1)∵侧面AA1B1B⊥底面ABC,侧棱AA1与底面ABC成600的角,
∴∠A1AB=600,又AA1= AB= 2,取AB的中点O,则AO⊥底面ABC.
以O为原点建立空间直角坐标系O-xyz如图,
则A(0,-1,0),B(0,1,0),C(![]() ,0,0),
,0,0),
A1(0,0,![]() )B1(0,2,
)B1(0,2,![]() ),C1(
),C1(![]() ,1,
,1,![]() ).… ……3'
).… ……3'
∵G为ΔABC的重心,∴G(![]() ,0,0),∵
,0,0),∵![]() =
=![]()
![]() ∴E(
∴E(![]() ,1,
,1,![]() )
)
∴![]() =(0,1,
=(0,1,![]() )=
)=![]()
![]() ,
,
又GE![]() 侧面AA1B1B,
∴GE∥侧面AA1B1B ………………
……7'
侧面AA1B1B,
∴GE∥侧面AA1B1B ………………
……7'
(2)设平面B1GE的法向量为![]() =(a,b,c),
=(a,b,c),
则由![]() ·
·![]() =0及
=0及![]() ·
·![]() =0得
=0得![]() a-b-
a-b-![]() c=0;b+
c=0;b+![]() c=0.
c=0.
可取![]() =(
=(![]() ,-1,
,-1,![]() ).
……………… ……………10'
).
……………… ……………10'
又底面ABC的法向量为![]() =(0,0,1),
……………… ……………12′
=(0,0,1),
……………… ……………12′
设平面B1GE与底面ABC所成锐二面角的大小为![]() ,
,
 则cos
则cos![]() =
=![]() =
=![]() , ∴
, ∴![]() =arccos
=arccos![]() . ……………… ……14′
. ……………… ……14′
 选项
选项