高二数学统考统阅试卷

高二数学统考统阅试卷（排列、组合和二项式定理）

　　　　　　　　　　　　　　　　　　　　　　　  200804

一、选择题（每小题5分，共50分）．

1.甲班有四个小组，每组10人，乙班有3个小组，每组15人，现要从甲、乙两班中选1人担任校团委部，不同的选法种数为（　　　）

A  80　　　　 　　　 B  84　　  　　　　C  85　　　　　　　　　 D　86

2．6人站成一排，甲、乙 、丙三人必须站在一起的排列种数为 　 （ 　　）

A．18　　　　　　 B．72　　　　　　  C．36　　　　　　　　 D．144

3．展开式的第7项是　 （　 　 ）

A 　　　　　　　 B —　　 　　　　C 　　　　　　　D —

4．用二项式定理计算，精确到1的近似值为（ 　　）

　A．99000　 　　　　  B．99002　　　　 C．99004　　　　　　　D．99005

5．不同的五种商品在货架上排成一排，其中甲、乙两种必须排在一起，丙、丁两种不能排在一起，则不同的排法种数共有（ 　 ）

A．12种　　 　　　B．20种　　　　　 C．24种　　 　　　　 D．48种

6．若展开式中含的项是第8项，则展开式中含的项是（　　 ）

　A．第8项　　　　　B．第9项　　　　C．第10项　　 　 　D．第11项

7．从4名男生和3名女生中选出4人参加某个座谈会，若这4人中必须既有男生又有女生，则不同的选法共有　　　　　 (　　  )

A　140种　　 　　　 B  34种　　　 　　　 C  35种　　　　　　 D  120种

9．已知展开式中常数项为1120，其中实数a是常数，则展开式中各项系数的和是（　 ）

　　　 A．2⁸　　　　　　　　　　　　　B．3⁸　　　　　　　　　　　　　 C．1或3⁸　　　　　　　　　　D．1或2⁸

10．某城市新修建的一条道路上有12盏路灯，为了节省用电而又不能影响正常的照明，可以熄灭其中的3盏灯，但两端的灯不能熄灭，也不能熄灭相邻的两盏灯，则熄灯的方法有（　　 ）

　A．种　　　　 B．种　　　 　　　C．种　　　　　　D．种

二、填空题（每小题5分，共25分）

11．设，则的值是　　　

12．不同的五种商品在货架上排成一排，其中甲、乙两种必须排在一起，丙、丁两种不能排在一起，则不同的排法种数共有__________．

13．的展开式中的系数为__________．（用数字作答）

若=32，则n =　　　　 。

14．用0，1，2，3，4组成没有重复数字的全部五位数中，若按从小到大的顺序排列，则数字12340应是第_________个数。

15．关于二项式(x-1)²⁰⁰⁵有下列命题： ①该二项展开式中非常数项的系数和是1：　 ②该二项展开式中第六项为Cx¹⁹⁹⁹； ③该二项展开式中系数最大的项是第1002项：④当x=2006时，(x-1)²⁰⁰⁵除以2006的余数是2005．其中正确命题的序号是__________ ．(注：把你认为正确的命题序号都填上)

三、解答题（本大题满分75分）

16（12分）已知展开式中偶数项的二项式系数之和为256，求x的 系数．

17．有5名男生，4名女生排成一排：

（1）从中选出3人排成一排，有多少种排法？

（2）若男生甲不站排头，女生乙不站在排尾，则有多少种不同的排法？

（3）要求女生必须站在一起，则有多少种不同的排法？

（4）若4名女生互不相邻，则有多少种不同的排法？

18．从7个不同的红球，3 个不同的白球中取出4个球，问：

（1）有多少种不同的取法？（2）其中恰有一个白球的取法有多少种？

（3）其中至少有现两个白球的取法有多少种？

19、(本题满分12分)　 已知展开式中偶数项二项式系数和比展开式中奇数项二项式系数和小，求：

（1）展开式中第三项的系数;（2）展开式的中间项。

20．（本小题满分12分）在二项式的展开式中，

（Ⅰ）若第5项，第6项与第7项的二项式系数成等差数列，求展开式中二项式系数最大的项；（Ⅱ）若前三项的二项式系数和等于79，求展开式中系数最大的项．

21．（本小题满分14分）有6名男医生，4名女医生。

（Ⅰ）选3名男医生，2名女医生，让这5名医生到5个不同地区去巡回医疗，共有多少种分派方法？

（Ⅱ）把10名医生分成两组，每组5人且每组要有女医生，则有多少种不同分法？若将这两组医生分派到两地去，并且每组选出正副组长两人，又有多少种分派方案？

参考答案

一选择题：

题号	1	2	3	4	5	6	7	8	9	10
答案	C	D	A	C	C	B	B	C	D	B

二、填空题：

11．.12　 　 24　　 13、　179　、 6　　14、　10 　 15、　①④　　　　 

三、解答题

16．解：由二项式系数的性质：二项展开式中偶数项的二项式系数之和为2^n－1，得n=9，由通项，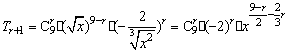

　　　 令，得r=3，所以x的二项式为=84，

　　　 而x的系数为．

17．（1）　 （2）287280 （3）17280　（4）2112

18．（1）210　（2）105　 （3）70

19．解：由题意得　　 即　 ∴，

　（1）展开式的第三项的系数为　　　　 

　（2）展开的中间项为　

20．解：（Ⅰ）　　∴n=7或n=14，

当n＝7时，展开式中二项式系数最大的项是T₄和T₅

且

当n＝14时，展开式中二项式系数最大的项是T₈

且　　 （Ⅱ），　 ∴n=12

设T_k+1项系数最大，由于

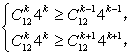　 ∴9.4<k<10.4，　 ∴k=10

21．解：（Ⅰ）（方法一）分三步完成．

第一步：从6名男医生中选3名有种方法；

第二步，从4名女医生中选2名有种方法；

第三步，对选出的5人分配到5个地区有种方法．

根据乘法原理，共有N==14400（种）．

（方法二）分二步完成．

第一步，从5个地区中选出3个地区，再将3个地区的工作分配给6个男医生中的2人，有种；

第二步，将余下的2个地区的工作分给4个女医生中的2个，有种．

根据乘法原理，共有N==14400（种）．

（Ⅱ）医生的选法有以下两类情况：

第一类：一组中女医生1人，男医生4人，另一组中女医生3人，男医生4人．共有种不同的分法；

第二类：两组中人数都是女医生2人男医生3人．因为组与组之间无顺序，故共有种不同的分法。

因此，把10名医生分成两组，每组5人且每组要有女医生的不同的分法共有+=120种不同分法。

若将这两组医生分派到两地去，并且每组选出正副组长两人，则共有

(+)=4800种分派方案。