高二数学选修1—2练习3

高二数学选修1—2练习（三）

（3.1数系的扩充与复数的概念，3.2复数代数形式的四则运算，4.1流程图，4.2结构图）

A组题（共100分）

一、选择题：本大题共5题，每小题7分，共35分。在每小题给出的四个选项中，只有一项是符合题目要求的。

1.是复数为纯虚数的（　 ）

A.充分不必要条件　　　B.必要不充分条件　　　C.充分必要条件　　D.既不充分也不必要

2. 复数的共轭复数是（　　）

A.i +2　　　B. i -2　　　C. -i -2　　　 D. 2 - i

3. 当时，复数在复平面内对应的点位于（　　）

　A. 第一象限　 B.第二象限 　　　C . 第三象限 　　　　 D.第四象限　　　

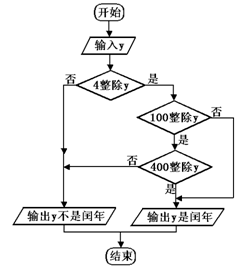4.如图是关于闰年的流程，则以下年份是闰年的为（ ）

　 A.1998年　　　　　　　  B.1994年

　 C. 2100年　　　　　　　 D.1996年

5.若实数，满足，则的值是（　 ）

　 A. 1　　B. 2　　 C.－2　　 D.－3

二、填空题：本大题共4小题，每小题6分，共24分。

6．流程图是用来描述具有　 特征的动态过程；结构图是一种描述　　 结构的图示。

7. 在复平面内，平行四边形ABCD的三个顶点A、B、C对应的复数分别是1+3i,-i,2+i,则点D对应的复数为　　　　　　　 。

8. 已知复数z与（z +2）² – 8 i 都是纯虚数，则z =_________。

9. 已知　　　　。

三、解答题：本大题共3小题，共41分，解答题应写出文字说明、证明过程或演算步骤。

10.已知，且 ，求z．（10分）

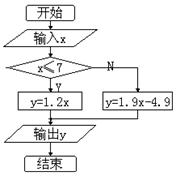
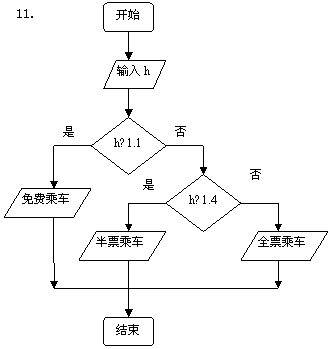
11.儿童乘坐火车时，若身高不超过1.1m，则无需购票；若身高超过1.1m但不超过1.4m，则购买半票乘车；若身高超过1.4m，则购买全票乘车；设计一个购票的算法流程图.

12．对任意正整数n，设计一个算法求的值，画出程序框图。

B组题（共100分）

一、选择题：本大题共5题，每小题7分，共35分。在每小题给出的四个选项中，只有一项是符合题目要求的。

13．复数z在复平面内所对应的点位于（　 ）

A．第一象限　　 B．第二象限　　C．第三象限　　　 D．第四象限

14．已知复数z满足则=（　　 ）

A．1　　 B. 0　　 C. 　　 D. 2

15．（　　）

A．1　　　　  B． 　　　　　 C．　　　　　　  D．　　　　　　　　　　　　　　　　　　

16．复数Z满足条件，与复数Z对应的点的图形是　（　 ）

A．圆　　 B．椭圆　　C．双曲线　　D．抛物线

17.读右边程序，若输入的为2008，5则输出的为（　 ）

A.16013　 B.31013　　　 C.258　　D.290

二、填空题：本大题共4小题，每小题6分，共24分。

18．设复数Z满足，则　　　　   。

19．设，，则的最大值是　　　　　 。

20．若关于的方程，则纯虚数　　  。

21．已知复数满足，则=　　 。

三．解答题：本大题共3小题，共41分，解答题应写出文字说明、证明过程或演算步骤。

22．已知：，

（1）证明：；　

（2）求值：；

（3）求值：。

23．已知方程

（1）若方程有实根，求θ及其两根；

（2）证明无论θ为何值，此方程不可能有纯虚根．

24．实数m分别取什么数时，复数是：

（1）实数；（2）虚数；（3）纯虚数；

（4）对应点在第三象限；

（5）对应点在直线上；

（6）共轭复数的虚部为12．

C组题（共50分）

一．选择或填空题：本大题共2题。每小题10分，共20分

25．根据右边程序框图，当输入10时，输出的是（　 ）

A．12　　B．19　　　　　　C．14.1 　　　　　 D．-30

26．图2是统计图1中身高在一定范围内学生人数的一个算法流程图　现要统计身高在160～180cm（含160cm，不含180cm）的学生人数，那么在流程图中的判断框内应填写的条件是（　 ）

Ａ　　　　　　　Ｂ　　　　　　　Ｃ　　　　　　　 Ｄ　

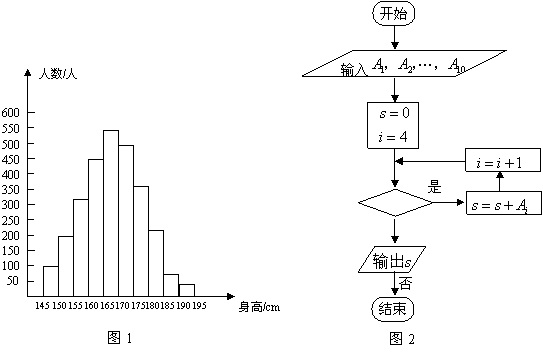二、解答题：本大题共2小题每小题15分，共30分，解答题应写出文字说明、证明过程或演算步骤。

27．（1）计算（其中i为虚数单位）

（2）设n是4的倍数，试求和：

参考答案

3.1数系的扩充与复数的概念，3.2复数代数形式的四则运算，4.1流程图，4.2结构图

A组题（共100分）

一．选择题：

1. B　　2. B　　3. D　　4.D　　5. A

二．填空题：

6．时间　系统　　；7.  ；　8. ；　 9.

三．解答题：

10．解：本题主要考查复数相等的充要条件及指数方程，对数方程的解法．

∵ ，∴，∴，

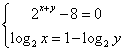解得或, ∴ z＝2＋i或z＝1＋2i．

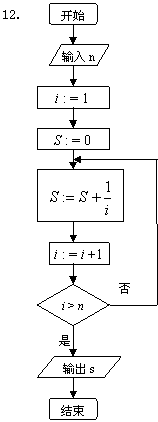
B组题（共100分）

一．选择题：

13．　　　14．　　　15． A　　 16． B　　17. B

二．填空题：本大题共4小题，每小题6分，共24分。

18． ；19． 3； 20． ； 21．

三．解答题：

22．（1）证明：∵

（2）

（3）

23．解：(1）设α∈R为方程的根，则有

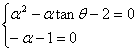
∴α=－1，tanθ=1

∴θ=kπ+，k∈Z．

设另一根为β，则(－1)·β=－(2+i)

∴β=2+i

∴θ=kπ+，k∈Z；两根分别为－1，2+i

(2)设bi为方程的纯虚根．(b∈R，b≠0)

则(bi)²－(tanθ+i)(bi)－(i+2)=0

∴

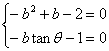
∵－b²+b－2=0，∴b²－b+2=0

∵此方程无实根，∴原方程无论θ为何值时，方程不可能有纯虚根．

24．解：z=(1+i)m²+(5－2i)m+6－15i=(m²+5m+6)+(m²－2m－15)i

∵m∈R，∴z的实部为m²+5m+6，虚部为m²－2m－15．

(1)若z是实数，则

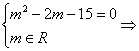m=5或m=－3

(2)若z是虚数，则

m²－2m－15≠0m≠5且m≠－3．

(3)若z是纯虚数，则

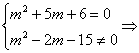m=－2

(4)若z的对应点在第三象限，则

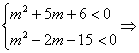－3<m<－2

(5)若z对应的点在直线x+y+5=0上，则(m²+5m+6）+(m²－2m－15)+5=0

 (6)若z的共轭复数的虚部为12，则－(m²－2m－15)=12m=－1或m=3．

C组题（共50分）

一、选择或填空题：

25．C　　 26．C

二、解答题：

27．解（1）

（2）解：∵S=1+2i+3i²+…+(n+1)iⁿ①

∴iS=i+2i²+…+niⁿ+(n+1)iⁿ⁺¹ ②

①－②得(1－i)S=1+i+i²+…+iⁿ－(n+1)iⁿ⁺¹=－(n+1)iⁿ⁺¹

∵n是4的倍数　　　∴iⁿ⁺¹=iⁿ·i=i

∴(1－i)S=－(n+1)i=1－(n+1)i

∴S=