高二数学选修1—2练习（二）
2.1合情推理与演绎推理，2.2直接证明与间接证明，
A组题（共100分）
一．选择题：本大题共5题，每小题7分，共35分．在每小题给出的四个选项中，只有一项是符合题目要求的．
1.如果数列
是等差数列，则（ ）
A.
B.
C.
D.
2.下面使用类比推理，得出正确结论的是 （ ）
A.“若
,则
”类推出“若
,则”
B.“若
”类推出“
”
C.“若” 类推出“
（c≠0）”
D.“
” 类推出“
”
3.有这样一段演绎推理：“有些有理数是真分数，整数是有理数，则整数是真分数”，
结论显然是错误的，是因为（ ）
A.大前提错误 B.小前提错误 C.推理形式错误 D.非以上错误
4.设
，
，n∈N，
则
（ ）
A.
B.－ C.
D.－
5.在十进制中
，那么在5进制中数码2004折合成十进制为 （ ）
A.29 B.
二．填空题：本大题共4小题，每小题6分，共24分．
6．由数列的前四项: 
,1 , 
,
,……归纳出通项公式an = ．
7. 类比平面几何中的勾股定理：若直角三角形ABC中的两边AB、AC互相垂直，则三角形三边长之间满足关系：
．若三棱锥A-BCD的三个侧面ABC、ACD、ADB两两互相垂直，则三棱锥的侧面积与底面积之间满足的关系为 .
8.从
中，可得到一般规律为 (用数学表达式表示)
9.设平面内有ｎ条直线
，其中有且仅有两条直线互相平行，任意三条直线不过同一点．若用
表示这ｎ条直线交点的个数，则
=
；
当ｎ＞４时，
＝
（用含n的数学表达式表示）
三．解答题：本大题共3小题，共41分，解答题应写出文字说明、证明过程或演算步骤．
10.证明：
不能为同一等差数列的三项.
11.在△ABC中，
，判断△ABC的形状.
12.已知：空间四边形ABCD中，E，F分别为BC，CD的中点，判断直线EF与平面ABD的关系，并证明你的结论.
B组题（共100分）
一．选择题：本大题共5题，每小题7分，共35分．在每小题给出的四个选项中，只有一项是符合题目要求的．
13．若a>0 , b>0 则有（ ）
A．
B. 
C. 
D. 
14．若
，且
，则
的最大值为（ ）
A．14 B.
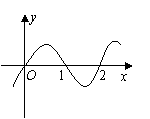15．已知函数
的图象如图所示，则有（ ）
A．b<0 B．0<b<1
C．1<b<2 D．b>2
16．下面几种推理是类比推理的是 （ ）
A．两条直线平行，同旁内角互补，如果∠
和∠
是两条平行直线的同旁内角，则∠+∠=1800
B．由平面三角形的性质，推测空间四边形的性质
C．某校高二级有20个班，1班有51位团员，2班有53位团员，3班有52位团员，由此可以推测各班都超过50位团员.
D．一切偶数都能被2整除，
是偶数，所以能被2整除.
17．已知
且
，则
不能等于（ ）
A．
B．
C．
D．
二．填空题：本大题共4小题，每小题6分，共24分．
18．若数列{
}，(n∈N
)是等差数列,则有数列b=
(n∈N)也是等差数列，类比上述性质，相应地：若数列{c}是等比数列,且c＞0(n∈N)，
则有d=
(n∈N)也是等比数列．
19．已知函数
，则
．
20．考察下列一组不等式：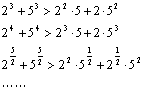
将上述不等式在左右两端仍为两项和的情况下加以推广，使以上的不等式成为推广不等式的特例，则推广的不等式为
．
21．若数列
的通项公式
，记
，试通过计算
的值，推测出
．
三．解答题：本大题共3小题，共41分，解答题应写出文字说明、证明过程或演算步骤．
22．设
都是正数，求证
．
23．三棱锥P-ABC中，平面PBC⊥平面ABC，△PBC是边长为a的正三角形，∠ACB=900，∠BAC=300，M是BC的中点．
（1）、求证：PB⊥AC． （2）、求点M到平面PCA的距离．
24．观察以下各等式：
，
分析上述各式的共同特点，猜想出反映一般规律的等式，并对等式的正确性作出证明．
猜想：
（14分）
C组题（共50分）
一．选择或填空题：本大题共2题．每小题10分，共20分
25．由图(1)有面积关系: 
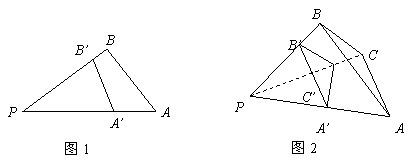则由(2) 有体积关系: 
26．设数列
的前n项和为
，令
，称
为数列
，
，……，
的“理想数”，已知数列，，……，
的“理想数”为2004，那么数列2， ，，……，的“理想数”为（ ）
A．2008 B．
二．解答题：本大题共2小题每小题15分，共30分，解答题应写出文字说明、证明过程或演算步骤．
27．已知函数
，当
时，值域为
，当
时，值域为
，…，当
时，值域为
，…．其中a、b为常数，a1=0，b1=1．
（1）若a=1，求数列{an}与数列{bn}的通项公式；
（2）若
，要使数列{bn}是公比不为1的等比数列，求b的值；
28．对于数列{an}，定义{△an }为数列{an}的一阶差分数列，其中
（1）若数列{an}的通项公式
的通项公式；
（2）若数列{an}的首项是1，且满足
，
①证明数列
为等差数列；
②求{an}的前n项和Sn ．
厦门市2007—2008学年选修1—2练习（二）参考答案
2.1合情推理与演绎推理，2.2直接证明与间接证明，
A组题（共100分）
一、选择题：
1．B 2．C 3．C 4．A 5．B
二、填空题：
6．
7．
8．
9．5 ； 
三、解答题
10.证明：假设
、
、
为同一等差数列的三项，则存在整数m,n满足
=+md ① =+nd ②
①
n-②m得：n-m=(n-m) 两边平方得： 3n2+
mn=2(n-m)2
左边为无理数，右边为有理数，且有理数
无理数
所以，假设不正确．即 、、不能为同一等差数列的三项
11.解：
ABC是直角三角形； 因为sinA=
据正、余弦定理得 ：（b+c）(a2-b2-c2)=0；
又因为a,b,c为ABC的三边，所以 b+c0
所以 a2=b2+c2 即ABC为直角三角形.
12. 证明：连接BD，因为E，F分别为BC，CD的中点， EF∥BD……..
B组题（共100分）
一、选择题：
13．C 14．B 15．A 16．B 17．D
二、填空题：
18．
19．1004
20．
21．
三．解答题：
22．证明：
23．①证明：∵∠ACB=900 ∴AC⊥BC
又∵平面PBC⊥平面ABC且交线为BC
∴AC⊥平面PBC 又∵PB
平面PBC ∴AC⊥PB
②解：连结PM∵M是正ΔPBC的BC边上的中点∴PM⊥BC
由①知AC⊥平面PBC 又AC平面PAC
∴平面PBC⊥平面PAC（一个平面过另一个平面的垂线，则这两个平面互相垂直） 作MH⊥PC交于PC于H ∴MH⊥平面PAC ∴MH就是点M到平面PAC的距离 在Rt△PMC中，MC=
，PM=
∴MH·PC=PM·MC ∴
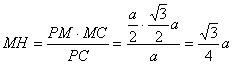
∴点M到平面PCA的距离为
24．证明：
C组题（共50分）
一．选择或填空题：
25．（
）
26． C
三．解答题：
27．解：⑴∵a＝1>0，∴f(x)＝ax＋b在R上为增函数，
∴an＝a·an－1＋b＝an－1＋b，bn＝bn－1＋b(n≥2)，
∴数列{an}，{bn}都是公差为b的等差数列．
又a1=0，b1=1,∴an=(n－1)b,bn＝1＋(n－1)b(n≥2) ……………………………7分
⑵∵a>0，bn＝abn－1＋b，∴，……………………………12分
由{bn}是等比数列知为常数．又∵{bn}是公比不为1的等比数列，则bn－1不为常数，
∴必有b＝0．………………………………………………15分
28．（1）依题意
，
∴ 
（2）①由
∴
，即
，∴
是以
为首项，为公差的等差数列 （8分）
②由①得
（10分）
∴
①
∴
②
①－②得 
∴
（15分）