高二数学选修2—2练习（二）
A组题（共100分）
(定积分的概念，1.6微积分基本定理，1.7定积分的简单应用)
一．选择题：本大题共5题，每小题7分，共35分。在每小题给出的四个选项中，只有一项是符合题目要求的。
1．下列值等于1的是 （ ）
A．
B．
C．
D．
2．
的值为（
）
A．0 B． 
C．2 D．4
3．
= （ ）
A．
B．2e
C．
D．
4．直线
与抛物线
所围成的图形面积是
（ ）
A．20 B．
C．
D． 
5．如果1N能拉长弹簧
A．0.18J B．0.26J C． 0.12J D．0.28J
二．填空题：本大题共4小题，每小题6分，共24分。
6．用定积分的几何意义，则
=_________
7.由曲线
所围成图形的面积是________.
8.若
，则k=
。
9. 计算
= 。
三.解答题：本大题共3小题，共41分，解答题应写出文字说明、证明过程或演算步骤。
10．计算下列定积分。（14分）
（1）
（2）
11．计算由曲线
，
所围成图形的面积。（13分）
12．求曲线
与
轴所围成的图形的面积．（14分）
B组题（共100分）
四．选择题：本大题共5题，每小题7分，共35分。在每小题给出的四个选项中，只有一项是符合题目要求的。
13．已知自由落体运动的速率
，则落体运动从
到
所走的路程为（ ）
A．
B．
C．
D．
14．
=（ ）
A．
B．
C．
D．
15．将和式的极限
表示成定积分（ ）
A．
B．
C．
D．
16． 若
，则k= ( )
A．1 B．
17．求由
围成的曲边梯形的面积时，若选择ｘ为积分变量，则积分区间为（ ）
A．［0，
］ B．［0，2］ C．［1，2］ D．［0，1］
五．填空题：本大题共4小题，每小题6分，共24分。
18. 若
是锐角
的一个内角，且
，则=
。
19．将和式
表示为定积分___________．
20按万有引力定律，两质点间的吸引力
，ｋ为常数，
为两质点的质量，ｒ为两点间距离，若两质点起始距离为ａ，质点
沿直线移动至离
的距离为ｂ处，试求所作之功（ｂ＞a）________________．
21. 计算
___________.
六．解答题：本大题共3小题，共41分，解答题应写出文字说明、证明过程或演算步骤。
22．一物体按规律x＝bt3作直线运动，式中x为时间t内通过的距离，媒质的阻力正比于速度的平方．试求物体由x＝0运动到x＝a时，阻力所作的功．
23．物体A以速度
在一直线上运动，在此直线上与物体A出发的同时，物体B在物体A的正前方
的速度与A同向运动，问两物体何时相遇？相遇时物体A的走过的路程是多少？（时间单位为：s，速度单位为：m/s）（15分）
24．求由抛物线
与过焦点的弦所围成的图形面积的最小值.
C组题（共50分）
七．选择或填空题：本大题共2题，每小题10分，共20分。
25．由
及
轴围成的介于0与2π之间的平面图形的面积，利用定积分应表达为_____________________．
26．将边长为
的液体中，使其上距液面距离为
八．解答题：本大题共2小题，解答题应写出文字说明、证明过程或演算步骤。
27．（15分）设y=f（x）是二次函数,方程f（x）=0有两个相等的实根，且f′（x）=2x+2.
（1）求y=f（x）的表达式；
（2）求y=f（x）的图象与两坐标轴所围成图形的面积.
（3）若直线x=－t（0＜t＜1＝把y=f（x）的图象与两坐标轴所围成图形的面积二等分，求t的值.
28．（15分）抛物线y=ax2＋bx在第一象限内与直线x＋y=4相切．此抛物线与x轴所围成的图形的面积记为S．求使S达到最大值的a、b值，并求Smax．
参考答案
A组题（共100分）
一、选择题：
1．C 2．C 3．D 4．C 5．A
二、填空题：
6．
7．
8．1
9． 
三、解答题：
10．(1) 
=
=
+
=
(2) 原式=
=
=1
11．解：为了确定图形的范围先求出两曲线的交点坐标
解方程组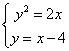
得出交点坐标(2,-2),(8,4)
因此,所求图形的面积
S=
=18
12．解：首先求出函数的零点：
，
，
.又易判断出在
内，图形在轴下方，在
内，图形在轴上方，
所以所求面积为
B组题（共100分）
四、选择题：
13．C 14．C 15．B 16．A 17．B
五、填空题：
18．
19．
20．
21．
六、解答题：
22．解：物体的速度
．
媒质阻力
，其中k为比例常数，k>0．
当x=0时，t=0；当x=a时，
，又ds=vdt，故阻力所作的功为
23．物体A以速度在一直线上运动，在此直线上与物体A出发的同时，物体B在物体A的正前方的速度与A同向运动，问两物体何时相遇？相遇时物体A的走过的路程是多少？（时间单位为：s，速度单位为：m/s）（15分）
23.设A追上B时,所用的时间为
依题意有
即
，
，=5 (s)
所以，
=
=130 (m)。
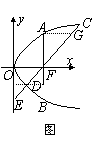24．解：焦点坐标为
，设弦AB、CD过焦点F，且
．
由图得知：
，故
．
所求面积为：
．
C组题（共50分）
七、选择或填空题：
25．
26．
八、解答题：
27．解：（1）设f（x）=ax2+bx+c，则f′（x）=2ax+b，
又已知f′（x）=2x+2
∴a=1，b=2.
∴f（x）=x2+2x+c
又方程f（x）=0有两个相等实根，
∴判别式Δ=4－
故f（x）=x2+2x+1.
（2）依题意，有所求面积=
.
（3）依题意，有
，
∴
，
－
t3+t2－t+=t3－t2+t，2t3－6t2+6t－1=0，
∴2（t－1）3=－1，于是t=1－
.
28．解 依题设可知抛物线为凸形，它与x轴的交点的横坐标分别为x1=0，x2=－b/a，所以
(1)
又直线x＋y=4与抛物线y=ax2＋bx相切，即它们有唯一的公共点，
由方程组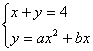
得ax2＋(b＋1)x－4=0，其判别式必须为0，即(b＋1)2＋
于是
代入（1）式得：
，
；
令S'(b)=0；在b＞0时得唯一驻点b=3，且当0＜b＜3时，S'(b)＞0；
当b＞3时，S'(b)＜0．故在b=3时，S(b)取得极大值，也是最大值，
即a=－1，b=3时，S取得最大值，且
．