高二数学选修2-2练习（一）
1.1变化率与导数，1.2导数的计算，
1.3导数在研究函数中的应用，1.4生活中的优化问题举例
A组题（共100分）
一．选择题（每题7分）
1.函数
的“临界点”是
A．1 B.
C．和1
D. 0
2．函数
的单调减区间是
A．（
B.
C．（， D.
3.
为方程
的解是为函数f(x)极值点的
A．充分不必要条件 B. 必要不充分条件
C．充要条件 D. 既不充分也不必要条件
4.函数
的图象如图所示，则导函数
的图象可能是
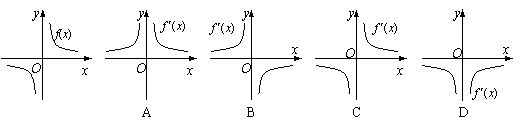5.福建炼油厂某分厂将原油精练为汽油,需对原油进行冷却和加热,如果第x小时时，原油温度（单位：
为
，那么，原油温度的瞬时变化率的最小值是
A．8 B. 
C． D.
二．填空（每题6分）
6、在高台跳水运动中，运动员相对于水面的高度h（单位：m）与起跳后的时间t（单位：S）存在关系h(t)= －4.9t
+6.5t+10,则起跳后1s的瞬时速度是
7、已知f
( x
)=－3,
则
=__________
8、函数f(x)=
的导数是f( x)=___________
9、Q是曲线C：f(x)=e
上的动点，当Q无限趋近于点P（0，1）时，割线PQ的斜率无限接近于一个常数是____________
三．解答题（13+14+14）
10、研究函数f(x)= x+3在x=1，2，3附近的平均变化率，哪一点附近的平均变化率最小.
11、已知f(x)=2sin
cos+2 cos2－1，求所有使f(x)+
f( x)=0成立的实数x的集合.
12. 
，且
（0.045,0.062）,贷款量与利率的平方成正比,因此,小陈申请这种一年期优惠贷款.
(1)写出小陈应支付的利息
;
(2) 一年期优惠利率为多少时,利息差最大?
B组题（共100分）
一．选择题（每题7分）
13．若函数
在R上是一个可导函数，则
在R上恒成立是在区间
内递增的
A．充分不必要条件 B. 必要不充分条件
C. 充要条件 D.既不充分也不必要条件
14．某产品的销售收入
(万元)是产量(千台)的函数：
，生产总成本
(万元)也是产量(千台)的函数；
，为使利润最大，应生产
A．6千台 B. 7千台 C．8千台 D.9千台
15．函数
(
,则
A．
B. 
C．
D.
大小关系不能确定
16、下列三个命题，正确的个数为（ ）
①加速度是动点位移函数S(t)对时间t的导数
②若f(x)=
,则f(0)=0
③曲线y=x
在点（0，0）处没有切线
A.0 B
17．
分别是定义在R上的奇函数和偶函数，当
时，
且
的解集为 （ ）
A．（－2，0）∪（2，+∞） B．（－2，0）∪（0，2）
C．（－∞，－2）∪（2，+∞）YCY D．（－∞，－2）∪（0，2）
二．填空：（每题6分）
18. 设
与
是函数
的两个极值点.则常数
= .
19．函数
在[1，+∞)上是单调递增函数，则的最大值是____________.
20．在半径为6的圆内，作内接等腰三角形，当底边上高为_________时它的面积最大.
21．设某种产品的成本与产量的函数关系是
,则产量为 时,该产品的边际成本最小.
三．解答题（13+14+14）
22．已知函数
，若函数在其定义域内为单调函数，求 的取值范围；
23．已知二次函数
经过点（2，4），其导数经过点（0，-5）和（2，-1），当
（
）时，
是整数的个数记为
。求数列
的通项公式；
24、如图,一水渠的横断面是抛物线形，O是抛物线的顶点,口宽EF=
（1） 建立适当的直角坐标系，求抛物线方程.
（2） 
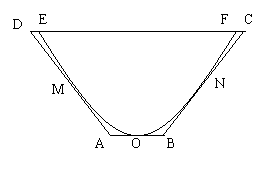现将水渠横断面改造成等腰梯形ABCD，要求高度不变，只挖土，不填土，求梯形ABCD的下底AB多大时，所挖的土最少？
C组题（共50分）
25.若＞3，则函数=
在(0，2)内恰有________个零点.
26．函数
，则
A．在
内是减函数 B. 在内是增函数
C．在
内是减函数 D.
在内是增函数
27.已知
为实数，且
,其中
为自然对数的底，求证：
28．设M是由满足下列条件的函数构成的集合：“①方程
有实数根；
②函数的导数
满足
.”
（I）判断函数
是否是集合M中的元素，并说明理由；
（II）集合M中的元素具有下面的性质：若的定义域为D，则对于任意
[m，n]
D，都存在[m，n]，使得等式
成立”，
试用这一性质证明：方程
只有一个实数根.
厦门市2007—2008学年选修2-2练习（二）参考答案
A组题（共100分）
1．C
2.D 3.D 4.D 5.C 6.-3.3
7.__6_
8. f(x)=
9. 1
10．解：在x=1附近的平均变化率是2+
在x=2附近的平均变化率是4+
在x=3附近的平均变化率是6+
∴在x=1附近的平均变化率是最小的
11．解：f(x)=sinx+cosx
所以f(x)= cosx-sinx
所以f(x)+ f(x)=(sinx+cosx)+(cosx-sinx)
由f(x)+ f(x)=0得2cosx=0
所以x=k
+
12.解：（1）由题意，贷款量为
(
，应支付利息=
（2）小陈的两种贷款方式的利息差为
令
=0，解得
或
当
所以，
时，利息差取得极大值，即一年期优惠利率为4.68%时,利息差最大.
B组题（共100分）
13.A 14.A 15. C 16. A 17.A
18．
19. 3
20．9 21.6
22．解： 
要使函数在定义域
内为单调函数，则在内恒大于0或恒小于0，
当
在内恒成立；
当
要使
恒成立，则
，解得
所以的取值范围为或
23.解：设
，将点（2，4）代入后，得
,将点（0，-5）和（2，-1）分别代入，得
b=-5,
解得
，c=10
所以
在（1，2］上的值域为［4，6），所以
在（2，3］上的值域为（
，4］，所以
当
时，在（n，n＋1］上单调递增，其值域为（
］
所以
所以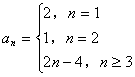
|
|
|
|
|
|
|
|
|
|
|
则F（2，3），设抛物线的方程是
因为点F在抛物线上，所以
所以抛物线的方程是
……………………4分
(2) 解：等腰梯形ABCD中,AB∥CD，线段AB的中点O是抛物线的顶点，AD，AB，BC分别与抛物线切于点M，O，N
，设
，
，则抛物线在N处的切线方程是
，所以
，……………………8分
梯形ABCD的面积是
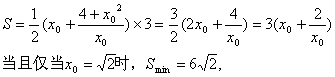……………………10分
答：梯形ABCD的下底AB=
米时，所挖的土最少.
C组题（共50分）
25. 1 26.A
27.
设f(x)=
(x＞e)，则f′(x)=
＜0,
∴函数f(x)在(e,+∞)上是减函数，又∵e＜a＜b,
∴f(a)＞f(b),即
,∴ab＞ba.
28．解：（1）因为
，
所以
满足条件
又因为当时，
，所以方程有实数根0.
所以函数是集合M中的元素.
（2）假设方程存在两个实数根
），
则
，
不妨设
，根据题意存在数
使得等式
成立
因为
，所以
与已知矛盾，所以方程只有一个实数根.