高二数学选修2—2练习（三）
2.1合情推理与演绎推理，2.2直接证明与间接证明，2.3数学归纳法
A组题（共100分）
一、选择题：本大题共5题，每小题7分，共35分．在每小题给出的四个选项中，只有一项是符合题目要求的．
1．用反证法证明命题：“三角形的内角中至少有一个不大于60度”时，反设正确的是（ ）．
A．假设三内角都不大于60度 B．假设三内角都大于60度
C．假设三内角至多有一个大于60度 D．假设三内角至多有两个大于60度
2．一同学在电脑中打出如下若干个圈:○●○○●○○○●○○○○●○○○○○●…
若将此若干个圈依此规律继续下去,得到一系列的圈,那么在前120个圈中的●的个数( )
A．12 B．
3．观察下列数:1,3,2,6,5,15,14,x,y,z,122,…中x，y，z的值依次是 ( )
A．42,，41，123 B．13，39，
4．下面几种推理过程是演绎推理的是 （ ）
A．两条直线平行，同旁内角互补，如果
和
是两条平行直线的同旁内角，则
．
B．由平面三角形的性质，推测空间四面体性质．
C．某校高三共有10个班，1班有51人，2班有53人，3班有52人，由此推测各班都超过50人．
D．在数列
中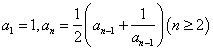
，由此归纳出的通项公式．
5．下面几种推理是合情推理的是 （ ）
（1）由圆的性质类比出球的有关性质；
（2）由直角三角形、等腰三角形、等边三角形内角和是
，归纳出所有三角形的内角和都是；
（3）某次考试张军成绩是100分，由此推出全班同学成绩都是100分；
（4）三角形内角和是，四边形内角和是
，五边形内角和是
，由此得凸多边形内角和是
A．（1）（2） B．（1）（3） C．（1）（2）（4） D．（2）（4）
二、填空题：本大题共4小题，每小题6分，共24分．
6．由数列的前四项：
，1 ，
，
，……，归纳出通项公式an =_______________．
7．若数列{
}，(n∈N
)是等差数列,则有数列b=
(n∈N)也是等差数列，类比上述性质，相应地：若数列{c}是等比数列,且c＞0(n∈N)，
则有d=_______ (n∈N)也是等比数列．
8．设
，利用课本中推导等差数列前
项和公式的方法，可求得
的值是________________．
9．利用数学归纳法证明“
”时，从“
”变到 “
”时，左边应增乘的因式是_____________________
三、解答题：本大题共3小题，共41分，解答题应写出文字说明、证明过程或演算步骤．
10．（14分）求证：(1)
; (2) 
+
>2
+
．
11．（13分）已知
，比较
与
的大小．
12．（14分）已知：
，求证：
（1）
；
（2）
中至少有一个不小于
．
B组题（共100分）
四、选择题：本大题共5题，每小题7分，共35分．在每小题给出的四个选项中，只有一项是符合题目要求的．
13．计算机中常用的十六进制是逢16进1的计数制，采用数字0~9和字母A~F共16个计数符号，这些符号与十进制的数字的对应关系如下表：
| 十六进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 十进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 十六进制 | 8 | 9 | A | B | C | D | E | F |
| 十进制 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
例如，用十六进制表示E+D=1B，则
（ ）
A． 6E B．
14．若数列
的前8项的值各异，且
对任意的
都成立，则下列数列中，可取遍的前8项值的数列是（ ）
A． 
B．
C．
D．
15．已知
表示平面，
表示直线，则
的一个充分条件是（ ）
A．
B．
C．
D．
16．设定义域为R的函数f(x)＝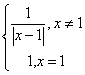
，若关于x的方程f2(x)＋bf(x)＋c＝0有3个不同的实数解x1、x2、x3，则
等于（ ）
A．5 B． C．13 D．
17．若
和g(x)都是定义在实数集R上的函数，且方程
有实数解，
则
不可能是
( )
A．
B．
C．
D．
五、填空题：本大题共4小题，每小题6分，共24分．
18．设函数是定义在R上的奇函数，且
的图像关于直线
对称，则
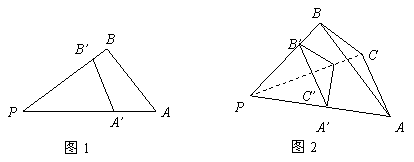
19．由图（1）有面积关系：
，则由图（2）有体积关系：
＝
．
20． 
，经计算的
，推测当
时，有_______．
21．设函数=(x-a)(x-b)(x-c),(a,b,c是两两不等的常数),则
+
+
的值是
．
六、解答题：本大题共3小题，共41分，解答题应写出文字说明、证明过程或演算步骤．
22．观察以下各等式：
，
分析上述各式的共同特点，猜想出反映一般规律的等式，并对等式的正确性作出证明．
23．（13分）否存在a、b、c使得等式1·22+2·32+…+n(n+1)2=
(an2+bn+c)．
24．（14分）已知
求证：
C组题（共50分）
七、选择或填空题：本大题共2题．每小题10分，共20分
25．设数列
的前n项和为
，令
，称
为数列
，
，……，
的“理想数”，已知数列，，……，
的“理想数”为2004，那么数列2， ，，……，的“理想数”为（ ）
A．2008 B．
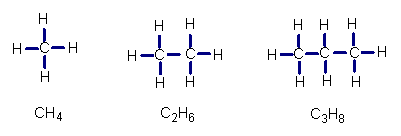26．．下列是三种化合物的结构式及分子式，请按其规律，写出后一种化合物的分子式是（ ）
A．C4H9 B．C4H
八、解答题：本大题共2小题每小题15分，共30分，解答题应写出文字说明、证明过程或演算步骤．
27．已知函数
，当
时，值域为
，当
时，值域为
，…，当
时，值域为
，…．其中a、b为常数，a1=0，b1=1．
（1）若a=1，求数列{an}与数列{bn}的通项公式；
（2）若
，要使数列{bn}是公比不为1的等比数列，求b的值；
28．问题1：求三维空间至多被个平面分割的区域数
．
问题
：求一个平面至多被条直线分割的区域数
．
问题
：求一直线至多被个点分成的段数
．
厦门市2007—2008学年数学选修2—2练习（三）参考答案
一、选择题：
1．B 2．C 3．A 4．A 5．C
二、填空题：
6．
7．
8．
9．
三、解答题：
10．（1） ∵
,
,
；
将此三式相加得
2
,∴．
（2）要证原不等式成立，只需证（+）
>（2+），即证
．
∵上式显然成立, ∴原不等式成立．
11解：∵
∴
∴
则 
又∵
，
∴
12．（1）证明：∵
∴
， 
， 
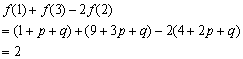
（2）假设
都小于
，
则
，
即有
，
，
∴ 
由（1）可知
，与矛盾，
∴假设不成立，即原命题成立．
B组题（共100分）
四、选择题：
13．A 14．B 15．D 16．D 17．D
五、填空题：
18．0 19．
20．
21．0
六、解答题：
猜想：
证明：
23．解:假设存在a、b、c使题设的等式成立，
这时令n=1,2,3,有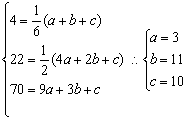
于是，对n=1,2,3下面等式成立
1·22+2·32+…+n(n+1)2=
记Sn=1·22+2·32+…+n(n+1)2
设n=k时上式成立，即Sk=
(3k2+11k+10)
那么Sk+1=Sk+(k+1)(k+2)2=
(k+2)(3k+5)+(k+1)(k+2)2
=
(3k2+5k+12k+24)
=［3(k+1)2+11(k+1)+10］
也就是说，等式对n=k+1也成立．
综上所述，当a=3,b=11,c=10时，题设对一切自然数n均成立．
24
证明：
，
C组题（共50分）
七、选择或填空题：
25．C 26．C
八、解答题：
27．解：⑴∵a＝1>0，∴f(x)＝ax＋b在R上为增函数，
∴an＝a·an－1＋b＝an－1＋b，bn＝bn－1＋b(n≥2)，
∴数列{an}，{bn}都是公差为b的等差数列．
又a1=0，b1=1,∴an=(n－1)b,bn＝1＋(n－1)b(n≥2) ……………………………7分
⑵∵a>0，bn＝abn－1＋b，∴，……………………………12分
由{bn}是等比数列知为常数．又∵{bn}是公比不为1的等比数列，则bn－1不为常数，
∴必有b＝0．………………………………………………15分
28．解：先考虑特殊情况：
，
，但凭借几何直观难以想象
的情况，于是转向考虑平面上类似问题．
先考虑特殊情况：
，
，
，
，但是随着直线数目的增多，情况越来越复杂，不能立即得出的一般表达式．于是，通过类比进一步考虑更简单的问题．
显然，这个问题易解决．
，
，…，
．
将以上讨论的结果整理成下表：
| 分割元素的数目 | 被割出的数目 | ||
| 空间被平面 | 平面被直线 | 直线被点 | |
|
| 2 | 2 | 2 |
| 2 | 4 | 4 | 3 |
|
| 8 | 7 | 4 |
| 4 | ? | 11 | 5 |
| … | ? | ? | … |
|
| ? | ? |
|
观察上表，发现
列中两列数之和，等于的下一列中的数字；
和列中的并列两数之和等于的下一行中的数字，于是归纳出一般的结论
：
，
．
这个结论是否正确？如果正确，又应怎样进行证明呢？
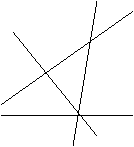
再从特殊情况进行分析：三条直线分成七个部分，
第四条直线
与前三条直线均相交，三个交点为
,
,
（图5－
12）．直线所穿过的区域均被分为两部分，于是增加的区域数就等于直线穿过的区域数，而直线穿过的区域数等于被点,,分成的段数
，于是，
．
对的分析，可以一字不差地适用于一般情况
图5－12
的证明．这样，
，
．
关于平面的表达式的推导也可以类比到三维空间，于是，
，
这样，刚开始提出的三个问题均得到圆满的解决．
当然，如果把记为
，那么，由，、的表达式可以归纳出更一般的结论；
维空间最多能被个
维平面分割的区域数
．