高二数学(文)第二学期期中考试
试题
考试时间:120分钟 试卷分值:150分
注意:本试卷包含Ⅰ、Ⅱ两卷。第Ⅰ卷为选择题,所有答案必须用2B铅笔涂在答题卡中相应的位置。第Ⅱ卷为非选择题,所有答案必须填在答题卷的相应位置。答案写在试卷上均无效,不予记分。
第Ⅰ卷(选择题 共60分)
一、选择题(本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一个是正确的。)
1.我校高中生共有2700人,其中高一年级900人,高二年级1200人,现采取分层抽样法抽取容量为135的样本,那么高一、高二、高三各年级抽取的人数分别为
A、45,75,15 B、 45,45,
2.有下列四个命题
①“若x+y=0 , 则x ,y互为相反数”的逆命题;
②“全等三角形的面积相等”的否命题;
③“若q≤1 ,则x2 + 2x+q=0有实根”的逆否命题;
④“不等边三角形的三个内角相等”逆命题;
其中真命题为
A.①② B.②③ C.①③ D.③④
3.经过点![]() 且与双曲线
且与双曲线![]() 有共同渐近线的双曲线方程为
有共同渐近线的双曲线方程为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.下列命题不正确的是
A 使用抽签法,每个个体被抽中的机会相等;
B 使用系统抽样从容量为N的总体中抽取容量为n的样本,确定分段间隔k时,若![]() 不是整数,则需随机地从总体中剔除几个个体;
不是整数,则需随机地从总体中剔除几个个体;
C 分层抽样就是随意的将总体分成几部分;
D 无论采取怎样的抽样方法,必须尽可能保证样本的代表性.
5.已知椭圆的焦点是F1、F2,P是随圆上的一个动点,如果延长F1P到Q,使得PQ=PF2, 那么动点Q的轨迹是
A.圆 B.椭圆 C.双曲线的一支 D.抛物线
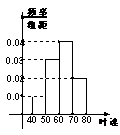 6.
6.![]() 辆汽车通过某一段公路时的时速的频率分布直方 图如右图所示,时速在
辆汽车通过某一段公路时的时速的频率分布直方 图如右图所示,时速在![]() 的汽车大约有
的汽车大约有
![]() .
.![]() 辆
辆
![]() .
.![]() 辆
辆
![]() .
.![]() 辆
辆
![]() .80辆
.80辆
7.如果命题P:![]() ,命题Q:
,命题Q:![]() ,那么下列结论不正确的是
,那么下列结论不正确的是
A.“P或Q”为真 B.“P且Q”为假
C.“非P”为假 D.“非Q”为假
|
A. B. C. D.
9.过双曲线![]() 的右焦点且方向向量为
的右焦点且方向向量为![]() 的直线L与抛物线
的直线L与抛物线![]() 交于A、B两点,则AB的值为
交于A、B两点,则AB的值为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.一个样本M的数据是![]() ,它的平均数是5,另一个样本N的数据是
,它的平均数是5,另一个样本N的数据是![]() 它的平均数是34.那么下面的结果一定正确的是
它的平均数是34.那么下面的结果一定正确的是
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
11.在120个零件中,一级品24个,二级品36个,三级品60个。用系统抽样法从中抽取容量为20的样本.则每个个体被抽取到的概率是
A. ![]() B.
B.![]() C.
C.![]() D.
D. ![]()
12.对于抛物线![]() 上任意一点Q,点P(a,0)都满足PQ≥a,则a的取值范围是
上任意一点Q,点P(a,0)都满足PQ≥a,则a的取值范围是
A.![]() B.
B.![]() C.[0,2] D.(0,2)
C.[0,2] D.(0,2)
第Ⅱ卷(非选择题 共90分)
二、填空题(本大题共4小题,每小题4分,共16分,把答案填在题中横线上。)
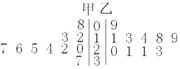 13.某篮球学校的甲、乙两名运动员练习罚球,每人
13.某篮球学校的甲、乙两名运动员练习罚球,每人
练习10组,每组罚球40个。命中个数的茎叶图如下.则
罚球命中率较高的是 。
14.命题“![]() ”的否定是
.
”的否定是
.
15.设全集S有两个子集A,B,若由x∈![]() SA
SA![]() x∈B,则x∈A是x∈
x∈B,则x∈A是x∈![]() SB的
条件.
SB的
条件.
16.已知抛物线![]() 上有一条长为2的动弦AB,则AB中点M到x轴的最短距离为
上有一条长为2的动弦AB,则AB中点M到x轴的最短距离为
.
三、解答题(共74分)
17.(本题满分12分)某种产品的广告费支出![]() 与销售额
与销售额![]() (单位:百万元)之间有如下对应数据:
(单位:百万元)之间有如下对应数据:
|
| 2 | 4 | 5 | 6 | 8 |
|
| 30 | 40 | 50 | 60 | 70 |
(1)画出散点图;
(2)求线性回归方程;
(3)预测当广告费支出为7百万元时的销售额。参考公式:
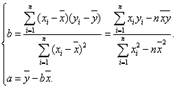
18.(本小题满分12分)
已知p:-x2+8x+20≥0,q:x2-2x+1-m2≤0(m>0).若“非p”是“非q”的充分不必要条件,求实数m的取值范围.
19.(本小题满分12分)下表是某中学对本校初中二年级女生身高情况进行抽测后所得的部分资料(身高单位:cm,测量时精确到
⑴ 求所有被测女生总数;
⑵ 求身高在
 ⑶ 完成频率分布直方图.
⑶ 完成频率分布直方图.
| 分 组 | 频 率 |
| [145.5,148.5) | 0.02 |
| [148.5,151.5) | 0.04 |
| [151.5,154.5) | 0.08 |
| [154.5,157.5) | 0.12 |
| [157.5,160.5) | 0.30 |
| [160.5,163.5) | 0.20 |
| [163.5,166.5) | 0.18 |
| [166.5,169.5] | 0.06 |
20.(本题满分12分)
在平面直角坐标系![]() O
O![]() 中,直线
中,直线![]() 与抛物线
与抛物线![]() =2
=2![]() 相交于A、B两点.
相交于A、B两点.
(1)求证:“如果直线![]() 过点T(3,0),那么
过点T(3,0),那么![]()
![]() =
=
(2)写出(1)中命题的逆命题,判断它是真命题还是假命题,并说明理由.
21.(本小题满分12分)
已知双曲线过点P![]() ,它的渐近线方程为
,它的渐近线方程为![]()
(1)求双曲线的标准方程;
(2)设F1和F2是这双曲线的左、右焦点,点P在这双曲线上,且PF1·PF2=32,求∠F1PF2的大小.
22.(本小题满分14分)
设![]() 、
、![]() ,
,![]() 、
、![]() 为直角坐标平面内x、y轴正方向上的单位向量,若向量
为直角坐标平面内x、y轴正方向上的单位向量,若向量![]() .
.
(1)求点M(x,y)的轨迹C的方程;
(2)过点(0,3)作直线L与曲线C交于A、B两点,设![]() ,是否存在这样的直线L,使得四边形OAPB是矩形?若存在,求出直线L的方程;若不存在,请说明理由.
,是否存在这样的直线L,使得四边形OAPB是矩形?若存在,求出直线L的方程;若不存在,请说明理由.
安徽省蚌埠五中07—08年高二第二学期期中考试
数学(文)参考答案及评分标准
一、选择题:
1.D 2.C 3.D 4.C 5.A 6.C 7.B 8.D 9.B 10.A
11.A 12.B
二、填空题:
13.甲 14.![]() 15.必要 16.
15.必要 16.![]()
三、解答题:
17.(1)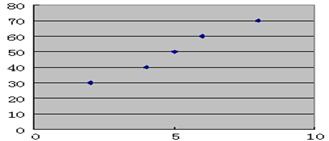
(2)b=7,a=15,ŷ=7x+15
(3)当x=7时,ŷ=64
18.(本小题满分13分)
已知p:-x2+8x+20≥0,q:x2-2x+1-m2≤0(m>0).若“非p”是“非q”的充分不必要条件,求实数m的取值范围.
解:p:![]() ,q:
,q:![]() 4分
4分
∵“非p”是“非q”的充分不必要条件
∴q是p的充分不必要条件 6分
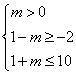
![]() 12分
12分
∴实数m的取值范围为![]() 。 13分
。 13分
19.解
⑴ =50(人)3分
⑵(0.2+0.18+0.06)×50=22(人) 6分
⑶要点:横轴:身高/cm;纵轴:频率/组距; 8分
长方形的高的比例:1:2:4:6:15:10:9:314分
20.证明:
(1)设过点T(3,0)的直线l交抛物线y2=2x于点A(x1,y1)、B(x12,y2).
当直线l的钭率下存在时,直线l的方程为x=3,此时,直线l与抛物线相交于点A(3,![]() )、B(3,-
)、B(3,-![]() ).∴
).∴![]() =3
=3
当直线l的钭率存在时,设直线l的方程为y=k(x-3),其中k≠0.
| 当 |
| 得ky2-2y-6k=0,则y1y2=-6. |
| y=k(x-3) |
又∵x1=![]() y
y![]() ,x2=
,x2=![]() y
y![]() ,
,
∴![]() =x1x2+y1y2=
=x1x2+y1y2=![]() =3.
=3.
综上所述,命题“如果直线l过点T(3,0),那么![]() =
=
(2)逆命题是:设直线l交抛物线y2=2x于A、B两点,如果![]() =3,那么该直线过点T(3,0).该命题是假命题.
=3,那么该直线过点T(3,0).该命题是假命题.
例如:取抛物线上的点A(2,2),B(![]() ,1),此时
,1),此时![]() =3,
=3,
直线AB的方程为Y=![]() (X+1),而T(3,0)不在直线AB上.
(X+1),而T(3,0)不在直线AB上.
说明:由抛物线y2=2x上的点A(x1,y1)、B(x12,y2)满足![]() =3,可得y1y2=-6.
=3,可得y1y2=-6.
或y1y2=2,如果y1y2=-6.,可证得直线AB过点(3,0);如果y1y2=2,可证得直线AB过点(-1,0),而不过点(3,0).
21.解(1)由渐近线方程知双曲线中心在原点,且渐近线上横坐标为![]() 的点
的点![]() 的纵坐
的纵坐
标绝对值为![]()
![]() ∴双曲线的焦点在
∴双曲线的焦点在![]() 轴上,设方程
轴上,设方程![]() 3分
3分
∵双曲线过点![]() ①
①
又![]() ②
②
由①②得![]() ,∴所求的双曲线方程为
,∴所求的双曲线方程为![]() 6分
6分
(2)证PF1=d1,PF2=d2,则d1·d2=32
又由双曲线的几何性质知d1-d2=
![]() 即有
即有![]() 10分
10分
又F![]()
△PF![]() 12分
12分
22.(1)解法一:![]() ,
,
∴点M(x,y)到两个定点F1(0,-2),F2(0,2)的距离之和为8.3分
∴轨迹C为以F1、F2为焦点的椭圆,方程为![]() ,5分
,5分
解法二:由题意知,![]() 2分
2分
移项,得![]() ,
,
两边平方,得![]() ,整理,得
,整理,得
![]() ,
,
两边平方,得![]() ,展开,整理得
,展开,整理得![]() .5分
.5分
(2)∵L过y轴上的点(0,3),若直线L是y轴,则A、B两点是椭圆的顶点.
∵![]() ,
,
∴P与O重合,与四边形OAPB是矩形矛盾,6分
∴直线L的斜率存在,设L方程为![]() .
.
由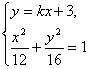 消去y得:
消去y得:![]() .8分
.8分
此时,![]() 恒成立.
恒成立.
且![]() .9分
.9分
![]() 四边形OAPB是平行四边形,
四边形OAPB是平行四边形,
若存在直线L,使得四边形OAPB是矩形,则![]() .
.
![]() ,11分
,11分
即![]() ,
,
也即![]() ,
,
即![]() .13分
.13分
∴存在直线L:![]() ,使得四边形OAPB是矩形.14分
,使得四边形OAPB是矩形.14分
17.(本小题满分12分)
已知双曲线过点P![]() ,它的渐近线方程为
,它的渐近线方程为![]()
(1)求双曲线的标准方程;
(2)设F1和F2是这双曲线的左、右焦点,点P在这双曲线上,且PF1·PF2=32,求
∠F1PF2的大小.
17.解(1)由渐近线方程知双曲线中心在原点,且渐近线上横坐标为![]() 的点
的点![]() 的纵坐
的纵坐
标绝对值为![]()
![]() ∴双曲线的焦点在
∴双曲线的焦点在![]() 轴上,设方程
轴上,设方程![]() 3分
3分
∵双曲线过点![]() ①
①
又![]() ②
②
由①②得![]() ,∴所求的双曲线方程为
,∴所求的双曲线方程为![]() 6分
6分
(2)证PF1=d1,PF2=d2,则d1·d2=32
又由双曲线的几何性质知d1-d2=
![]() 即有
即有![]() 10分
10分
又F![]()
△PF![]() 12分
12分
19.(本小题满分12分)
已知抛物线顶点在原点,焦点在x轴上,又知此抛物线上一点A(4,m)到焦点的
距离为6.
(1)求此抛物线的方程;
(2)若此抛物线方程与直线![]() 相交于不同的两点A、B,且AB中点横坐标为2,
相交于不同的两点A、B,且AB中点横坐标为2,
求k的值.
19.解:(1)由题意设抛物线方程为![]() ,其准线方程为
,其准线方程为![]() ,2分
,2分
∵A(4,m)到焦点的距离等于A到其准线的距离
![]() ∴此抛物线的方程为
∴此抛物线的方程为![]() 6分
6分
(2)由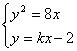 消去
消去![]() 8分
8分
∵直线![]() 与抛物线相交于不同两点A、B,则有
与抛物线相交于不同两点A、B,则有![]() 10分
10分
解得![]() 解得
解得![]() (舍去)
(舍去)
∴所求k的值为212分
20.(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分)
在平面直角坐标系![]() O
O![]() 中,直线
中,直线![]() 与抛物线
与抛物线![]() =2
=2![]() 相交于A、B两点.
相交于A、B两点.
(1)求证:“如果直线![]() 过点T(3,0),那么
过点T(3,0),那么![]()
![]() =
=
(2)写出(1)中命题的逆命题,判断它是真命题还是假命题,并说明理由.
21.证明:
(1)设过点T(3,0)的直线l交抛物线y2=2x于点A(x1,y1)、B(x12,y2).
当直线l的钭率下存在时,直线l的方程为x=3,此时,直线l与抛物线相交于点A(3,![]() )、B(3,-
)、B(3,-![]() ).∴
).∴![]() =3
=3
当直线l的钭率存在时,设直线l的方程为y=k(x-3),其中k≠0.
| 当 |
| 得ky2-2y-6k=0,则y1y2=-6. |
| y=k(x-3) |
又∵x1=![]() y
y![]() ,x2=
,x2=![]() y
y![]() ,
,
∴![]() =x1x2+y1y2=
=x1x2+y1y2=![]() =3.
=3.
综上所述,命题“如果直线l过点T(3,0),那么![]() =
=
(2)逆命题是:设直线l交抛物线y2=2x于A、B两点,如果![]() =3,那么该直线过点T(3,0).该命题是假命题.
=3,那么该直线过点T(3,0).该命题是假命题.
例如:取抛物线上的点A(2,2),B(![]() ,1),此时
,1),此时![]() =3,
=3,
直线AB的方程为Y=![]() (X+1),而T(3,0)不在直线AB上.
(X+1),而T(3,0)不在直线AB上.
说明:由抛物线y2=2x上的点A(x1,y1)、B(x12,y2)满足![]() =3,可得y1y2=-6.
=3,可得y1y2=-6.
或y1y2=2,如果y1y2=-6.,可证得直线AB过点(3,0);如果y1y2=2,可证得直线AB过点(-1,0),而不过点(3,0).