高二数学（理）第一学期期终三校联考试题
命题人：临泉一中 周河山
一、选择题：（每小题5分，共55分，每小题只有一项符合题意。）
1、设原命题：若a+b≥2，则a、b中至少有一个不小于1，原命题与其逆命题的真假情况是（ ）。
A．原命题真，逆命题假 B．原命题假，逆命题真
C．原命题与逆命题均为真命题 D．原命题与逆命题均为假命题
2、设等比数列{an}的前n项和为Sn，若a2008=2S2007+6, a2009=2S2008+6, 则数列{an}的公比q为（ ）。
A．2 B．
3、椭圆
+
=1与双曲线
-
=1有共同的焦点，则椭圆的离心率为（ ）。
A．
B．
C．
D．
4、△ABC中，角A、B的对边分别是a、b，且A=2B，则
的取值范围是（ ）。
A．（1，2） B．（0，
） C．（
，1） D．（0，2）
5、正方体ABCD—A1B
A． B．
C．1
D．
6、已知A（1，0，0）， B（0，-1，1），
+
与
的夹角为120°，则
的值为（ ）。
A．±
B． C．- D．±
7、已知
、
为任意非零向量，有下列命题：
（1）=；（2）（）2=（）2；（3）（）2=·
其中可以作为=的必要且非充分条件的命题是（ ）。
A．（1） B．（1）（2） C．（2）（3） D．（1）（2）（3）
8、原点O和点P（1，1）在直线x+y-a=0的两侧，则a的取值范围为（ ）。
A．a﹤0或a﹥2
B．a=0或a=
9、某圆锥曲线C是椭圆或双曲线，若其中心为坐标原点，对称轴为坐标轴，且过点
A（-2，2），B（
，-
），则（ ）。
A．曲线C可为椭圆也可为双曲线 B．曲线C一定是双曲线
C．曲线C一定是椭圆
D．这样的曲线C不存在
10、对于每个自然数n，抛物线y=(n2+n)x2-(2n+1)x+1与x轴交于An、Bn两点，以AnBn表示该两点间的距离，则A1B1+A2B2+…+A2008B2008的值是（ ）。
A．
B．
C．
D．
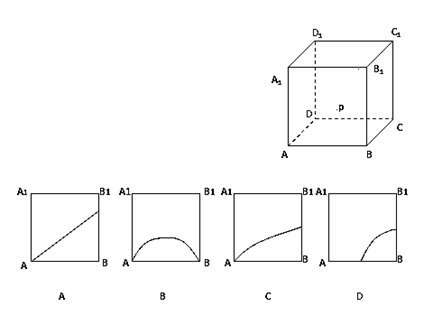
11、如图所示，在正方体ABCD—A1B
线A1B1与直线BC的距离相等，则动点P所在曲线形状为（ ）。
二、填空题：（每小题4分，共16分）
12、在△ABC中，AB=，AC=1，∠B=30°，则△ABC的面积为______________。
13、定义“等积数列”：在一个数列中，如果从第二项起每一项与它的前一项的积都为一个常数，那么这个数列称为等积数列，这个常数称为该数列的公积。已知数列{an}是等积数列，且a4=2,公积为8，那么a2009=______________。
14、若直线y=kx-1与双曲线x2-y2=4,有两个公共点，k的了值范围是___________。
15、已知两个变量x、y之间的关系为lg(y-x)=lgy-lgx，则以x为自变量的函数y的最小值为____________。
三、解答题：（本大题共6小题，满分79分。解答应写出文字说明、证明过程或演算步骤。）
16、（10分）设p：方程
+
=1表示双曲线，q：方程3x2+2mx+m+
=0有两个不同的实根，求使“p且q”为真命题的m的取值范围。
17、（13分）在△ABC中，a、b、c分别为角A、B、C的对边的长，若a=3,c=7,且sin。求△ABC的面积。
18、（14分）已知双曲线
-y2=1,过点P(0,1)作斜率k﹤0的直线L与双曲线恰有一个交点,（1）求直线L的方程；
（2）若点M（x,y）在所有直线L与y=0所围成的平面区域（包括边界）内运动，求Z=-x+y的最小值。
 |
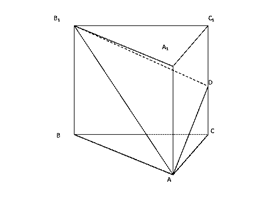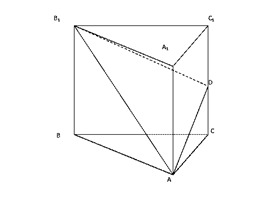
19、（14分）如图，正三棱柱ABC—A1B
CC1的中点。
（1）求直线AB1，A
（2）证明：A1B⊥平面AB1D；
（3）点A1到平面AB1D的距离。
20、（14分）已知Pn(an,bn)都在直线L:y=2x+2上，P1为直线L与x轴的交点，数列{an}是
等差数列，公差为1（n∈N*）。
（1）求数列{an}，{bn}的通项公式；
an(n为奇数)
（2）若f(n)=
问是否存在k∈N*,使得f(k+5)=
bn（n为偶数）
求出k的值；若不存在，说明理由。
（3）求证：
+
+…+
﹤
（n≥2,n∈N*）
21、(14分)如图，F1，F2分别是椭圆
+
=1（a﹥b﹥0）的左、右焦点，M为椭圆上一点，MF2垂直于x轴,且OM与椭圆长轴和短轴端点连线AB平行。
（1）求椭圆的离心率；
（2）若G为椭圆上不同于长轴端点的任一点，求∠F1GF2的取值范围；
（3）过F2且与OM垂直的直线交椭圆于P、Q，若S△PF1Q=20，求椭圆的方程。
三校联考试题答卷
一、选择题：（每小题5分，共55分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 答案 |
二、填空题：（每小题4分，共16分）
12、___________________________________ 13、__________________________________
14、___________________________________ 15、__________________________________
三、解答题：
16、（10分）
17、（13分）
18、（14分）
 |
19、（14分）
20、（14分）
21、（14分）
高二数学（理）期终试题参考答案
一、选择题：
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 答案 | A | D | B | A | B | C | D | D | B | D | C |
二、填空题：
12、
或
13、4 14、（-
，-1）∪（-1，1）∪（1，） 15、4
三、解答题：
16、（10分）
解：∵+=1 表示双曲线
∴(1
（4分）
∵方程3x2+2mx+m+=0有两个不同的实根
∴△=)﹥0
解得：m﹤-1或m﹥4 （8分）
要使“p且q”为真命题，则有m﹤-2或m﹥4
即m的取值范围是：（-∞，-2）∪（4，+∞） （10分）
17、（13分）
解：由sin,可得：cos
又C∈(0,
), 故)
∴
或
，即C=
或
（3分）
若C=,由cosC=
=
=
得：b2-3b-40=0, ∴b=8或b=-5(舍去)
此时△ABC的面积为absinC=6
（8分）
若C=,由cosC===-
得：b2-3b-40=0, ∴b=5或b=-8(舍去)
此时△ABC的面积为absinC=
。
（13分）
18、（14分）
解：（1）由已知得l:y=kx+1
y=kx+1
解方程组：
(1-2k2)x2-4kx-4=0
-y2=1
当1-2k2=0时，又k﹤0得：k=-,此时x=
直线L与双曲线恰有一个交点 L：y=-x+1 （5分）
当1-2k2≠0时，由△=16k2+16(1-2k2)=0 得：k=-1(k﹤0)
得 L:y=-x+1
∴直线L的方程为：y=-x+1或y=-x+1
（8分）
(2)由所有直线L与y=0所围成的平面区域如图
其中A（1，0），B（0，1），C（，0）
作直线L0:-x+y=0,并平移得直线L
当直线L过点C时，Z有最小值
Zmin=-。
（14分）
19、（14分）
（1）以BC中点O为原点，以OA、BC所在直线分别为x轴、y轴，以过O点在BC1面内垂直于BC的直线为Z轴建立空间直角坐标系0-xyz。
则得：A（，0，0），B1（0，-，1），A1（，0，1）
C（0，，0）， D（0，，）， B（0，-，0）
∴
=（-，-，1）， 
=（-，，-1）
·=
-
-1=-
=
=，A
∴cos<, > =
=
=-
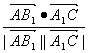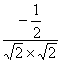∴直线AB1，A。
(5分)
（2）由已知AA1B1B为正方形，A1B⊥AB1
又由（1）知
=（-，-，-1），
=（-，，）
∴·=（-）2+（-）·（）+（-1）×=0
∴A1B⊥AD，又AB1∩AD=A
∴A1B⊥平面AB1D。 （9分）
（3）由（1）知：=（-，，），
=（0，1，-）
=（0，0，-1）
设
=（x,y,1）是平面AB1D的法向量
·=0
-x+
+=0
x=
则 得： 解得：
·=0
y-=0
y=
∴=(,,1), 
=
=（，，1）
则A1到平面AB1D的距离d=·
=。
（14分）
20、（14分）
解：（1）P1（-1，0），an=-1+(n-1)·1=n-2, bn=2(n-2)+2=2n-2 （4分）
n-2(n为奇数)
（2）f(n)= 如果存在符合条件的k。
2n-2（n为偶数）
①若k为偶数，则k+5为奇数，有f(k+5)=k+3, f(k)=2k-2
如果f(k+5)=k=3
与k为偶数不符，不存在。
②若k为奇数，则k+5为偶数，有f(k+5)=2k+8, f(k)=k-2
如果f(k+5)=
故不存在符合条件的k。 （9分）
（3）∵Pn(n-2,2n-2)
∴P1Pn=(n-1) (n≥2)
∴++…+=
[1+
+
+…+
]
﹤[1+
+
+…+
]=（1+1-
）﹤。 （14分）
21、（14分）
（1）由已知M（c, 
）, ∵kOM=kAB ,
∴
=
, ∴b=c, e=
=
（2）设GF1=m, GF2=n, 
=∠F1GF2, cos=
=
=
-1≥
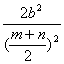-1=0
当且仅当m=n时，（cos）min=0, ∴∈(0, 
]
（9分）
y=- (x-c)
（3） b2x2+a2y2=a2b2 5y2-2cy
a=c, b=c
y1-y2=
=
c
S△PF1Q=F×c=20
∴c2=b2=25, a2=50,
∴椭圆的方程为：
+
=1
（14分）