高二数学(理)第二学期期中测验
试卷
第Ⅰ卷(选择题,共40分)
一、选择题:本大题共有8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的。(注:答案请填涂在答题卷里)
1、复数![]() 的共轭复数是( )。
的共轭复数是( )。
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
2、复数![]() 在复平面内表示的点在( )。
在复平面内表示的点在( )。
(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限
3、“因指数函数![]() 是增函数(大前提),而
是增函数(大前提),而![]() 是指数函数(小前提),所以
是指数函数(小前提),所以![]() 是增函数(结论)”,上面推理的错误是(
)。
是增函数(结论)”,上面推理的错误是(
)。
(A)大前提错导致结论错 (B)小前提错导致结论错
(C)推理形式错导致结论错 (D)大前提和小前提错都导致结论错
4、若![]() ,则
,则![]() 时,
时,![]() 是( )。
是( )。
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)非以上答案
(D)非以上答案
5、函数![]() 在
在![]() 上的最大值和最小值分别是(
)。
上的最大值和最小值分别是(
)。
(A)![]() ,
,![]() (B)
(B)![]() ,
,![]() (C)
(C)![]() ,
,![]() (D)
(D)![]() ,
,![]()
6、![]() 的展开式中系数最大的项是( )。
的展开式中系数最大的项是( )。
(A)第5项 (B)第6项 (C)第7项 (D)第8项
7、不同的五种商品在货架上排成一排,其中![]() ,
,![]() 两种必须排一起,而
两种必须排一起,而![]() ,
,![]() 两种不能排在一起,则不同的排法共有( )。
两种不能排在一起,则不同的排法共有( )。
(A)12种 (B)20种 (C)24种 (D)48种
8、设![]() ,则
,则![]() 的值为( )。
的值为( )。
(A)1 (B)16 (C)15 (D)-15
第Ⅱ卷(非选择题,共110分)
二、填空题:本大题共需要做6小题(第13、14、15三小题,学生只需要选做其中两小题,三小题都做的只计算第13、14小题的得分),每小题5分,共30分。(注:把答案填在答题卷相应位置)
9、若![]() 是实数,
是实数,![]() 是纯虚数,且满足
是纯虚数,且满足![]() ,则
,则![]() ,
,![]() 。
。
10、![]() 的展开式中
的展开式中![]() 的系数是
。(结果用数值表示)
的系数是
。(结果用数值表示)
11、若函数![]() 在
在![]() 上没有极值点,则实数
上没有极值点,则实数![]() 的取值范围是
。
的取值范围是
。
12、![]() =
。
=
。
13、在![]() 的展开式中,若存在常数项,则正整数
的展开式中,若存在常数项,则正整数![]() 的最小值为
。
的最小值为
。
14、从![]() 中,可得一般规律为
。
中,可得一般规律为
。
15、组织一支10人球队,由七所学校的学生组成,每所学校至少有一人,名额分配方案的种数为 。(结果用数值表示)
三、解答题:本大题共6小题,共80分。解答应写出文字说明,证明过程或演算步骤。
16、(本小题满分13分)求曲线![]() 与
与![]() 围成的平面图形的面积。
围成的平面图形的面积。
17、(本小题满分13分)计算:![]() +
+![]()
18、(本小题满分13分)设![]() 在
在![]() 与
与![]() 时都取得极值,试确定
时都取得极值,试确定![]() 与
与![]() 的值;此时
的值;此时![]() 在
在![]() 处取得的是极大值还是极小值?
处取得的是极大值还是极小值?
19、(本小题满分13分)已知![]() ,并且
,并且![]() ,用分析法证明:
,用分析法证明:![]()
20、(本小题满分14分)对于数列![]() ,
,![]() ,且
,且![]() ,
,![]() ;
;
(1)求![]() ,并猜想这个数列的通项公式;
,并猜想这个数列的通项公式;
(2)用数学归纳法证明你的猜想。
21、(本小题满分14分)已知函数![]() (
(![]() 、
、![]() 为常数);
为常数);
(1)若![]() 在
在![]() 和
和![]() 处取得极值,试求
处取得极值,试求![]() 、
、![]() 的值;
的值;
(2)若![]() 在
在![]() 上单调递增且在
上单调递增且在![]() 上单调递减,又满足
上单调递减,又满足![]() >1,求证:
>1,求证:![]() ;
;
(3)在(2)的条件下,若![]() ,试比较
,试比较![]() 与
与![]() 的大小,并加以证明。
的大小,并加以证明。
2007—2008学年度江门市四校联考第二学期期中测验 高二数学(理)试卷
参考答案及评分标准
三、选择题:本大题共有8小题,每小题5分,共40分
BBACA DCD
四、填空题:本大题共需要做6小题(第13、14、15三小题,学生只需要选做其中两小题,三小题都做的只计算第13、14小题的得分),每小题5分,共30分。
9、![]() ;
;![]() 10、40 11、[-
10、40 11、[-![]() ,
,![]() ]
12、
]
12、![]()
13、5
14、![]() 15、84
15、84
三、解答题:本大题共6小题,共80分。解答应写出文字说明,证明过程或演算步骤。
16、(本小题满分13分)
解:如图所示,解方程组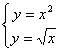 得
得 ![]() 或
或![]() ……5分
……5分
∴曲线![]() 与
与![]() 围成的平面图形的面积为:
围成的平面图形的面积为:
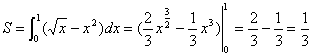 ……13分
……13分
17、(本小题满分13分)
解:原式=![]() ……5分
……5分
=![]() ……10分
……10分
=![]()
![]() ……12分
……12分
= i-i
= 0 ……13分
18、(本小题满分13分)
解:函数的定义域为(0,+∞)
∵![]() =
=![]() +2bx+1
……3分
+2bx+1
……3分
由已知x=1与x=2是函数的极值点
∴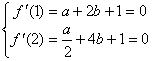 ,解得
,解得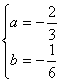 ……7分
……7分
∴![]() =
=![]() ……9分
……9分
令![]() >0,解得1<x<2;令
>0,解得1<x<2;令![]() <0,解得0<x<1或 x>2
……11分
<0,解得0<x<1或 x>2
……11分
(用列表分析方法得到极值点)
∴函数![]() 在
在![]() 处取得的是极小值。 ……13分
处取得的是极小值。 ……13分
19、(本小题满分13分)
证明: ∵![]() ,∴
,∴![]()
要证![]()
只需证![]() ……5分
……5分
只需证![]()
只需证![]()
又![]() ∴只需证
∴只需证![]() ……11分
……11分
由题设可知![]() 显然成立,所以
显然成立,所以![]() 得证
……13分
得证
……13分
20、(本小题满分14分)
解:(1)∵![]() ,且
,且![]() ,
,
![]()
∴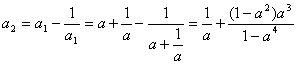
![]()
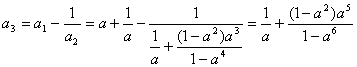
![]()
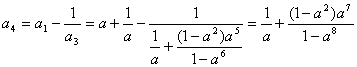
![]()
……4分
猜想数列的通项公式为![]() ……6分
……6分
![]()
(2)证明:①当![]() 时,
时,![]() ,
,![]() ,显然成立…7分
,显然成立…7分
②假设当![]() 时,猜想成立,即
时,猜想成立,即![]() ……9分
……9分
则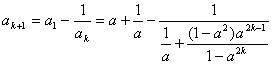
![]()
![]()
![]()
∴当![]() 时,猜想也成立
……13分
时,猜想也成立
……13分
综合①②可证猜想对![]() 都成立
……14分
都成立
……14分
21、(本小题满分14分)
解:(1)![]()
由题意得,1和3是方程![]() 的两根,
的两根,
∴![]() 解得
解得![]() ……4分
……4分
(2)由题意得,
当![]() 时,
时,![]()
当![]() 时,
时,![]()
∴![]() 是方程
是方程![]() 的两根,
的两根,
则![]() , ……6分
, ……6分
∴![]()
![]()
![]()
∵![]() ∴
∴![]()
∴![]() . ……9分
. ……9分
(3)在(2)的条件下,由上一问知
![]()
即![]()
所以![]() ……12分
……12分
∵![]() ∴
∴![]()
又![]() ∴
∴![]()
∴![]()
即![]() ……14分
……14分