高二数学上册期中考试模拟试题
姓名 班级编号 分数
一、选择题（本大题共10小题，每小题5分，共50分）
1.已知M＝｛正四棱柱｝，N＝｛长方体｝，Q＝｛正方体｝，P＝｛直四棱柱｝．则下列关系中正确的是（ ）
A．
B．
C．
D．
2.若
、
表示直线，
表示平面，则下列命题中，正确的个数为（ ）
①
②
③
④
A．1个 B．2个 C．3个 D．4个
3.下列命题中，假命题的是（ ）
A．如果平面
内有两条相交线与平面
内的两条相交线对应平行，则//；
B．空间一点
位于平面
内的充要条件是存在有序实数对
，对空间任一定点
有
；
C．如果平面内有无数条直线都与平面平行，则//；
D．若点是线段
的中点，则
满足向量表示式
；
4.设A，B，C，D是空间不共面的四点，且满足
，
，
，则△BCD是( )
A．钝角三角形 B．直角三角形 C．锐角三角形 D．不确定
5. 已知一个简单多面体的每个面均为五边形，且它共有30条棱，则此多面体的面数F和顶点数V分别等于（ ）
A．F=6，V=26
B．F=20，V=
6.已知球
的球面上一点，过点有三条两两互相垂直的直线，分别交球的球面于
、
、
三点，且
2、
2、
4，则球的体积为( )
A．
B．
C．
D．
7. 在棱长为2的正方体中，动点P在ABCD内，且P到直线AA1，BB1的距离之和等于
，则ΔPAB的面积最大值是（ ）
A．
B．
8. 已知空间四点 A（2，1，-3），B（-2，3，-4），C（3，0，1），D（1，4，m），若A、B、C、D四点共面，则m=（ ）
A．-7
B．
9. 将∠B=60o且边长为1的菱形ABCD沿对角线AC折成大小为
的二面角，若
，则折后两条对角线AC和BD之间的距离为 ( )
A．最小值为
，最大值为
B．最小值为，最大值为
C．最小值为
，最大值为
D．最小值为，最大值为
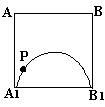
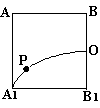
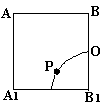
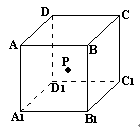10. 如图所示，在正方体ABCD—A1B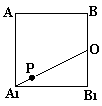
A
B
C
D
答 题 卡
| 题 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答 案 |
|
|
|
|
|
|
|
|
|
|
二、填空题（本大题共5小题，每小题5分，共25分）
11.判断
与
的大小关是： 。（填
、
、
、或不确定）
12.棱长为1的正方体
中，
、
分别是
、
的中点，则点到平面
的距离是 。
13.有一山坡，其倾斜角为
，如在斜坡上沿一条与坡底线成
的道上山，每向上升高
14.一个三棱锥的三个侧面中有两个等腰直角三角形，另一个是边长为1的正三角形，这样的三棱锥体积为 。（写出一个你认为可能的值即可）
15.四面体ABCD中，有如下命题：①若AC⊥BD，AB⊥CD，则AD⊥BC；②若E、F、G分别是BC、AB、CD的中点，则∠FEG的大小等于异面直线AC与BD所成角的大小；③若点O 是四面体ABCD外接球的球心，则O 在面ABD上的射影是△ABD的外心；④若四个面是全等的三角形，则ABCD为正四面体，其中正确的是： .（填上所有正确命题的序号）
三、解答题（本大题共6小题，满分75分）
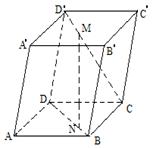
16.（本题12分）已知如图，在平行六面体
中，
分对角线
的比为
，
为
的比为
，设
。（1）试有
表示
（2）若
，且
，
求
的长度。
17.（本题12分）5人站成一排．（1）有多少种不同排法?（2）甲不能站排头,乙不能站排尾,有多少种排法?（3）甲乙必须相邻,有多少不同排法?（4）甲乙不能相邻有多少不同排法?
18.（本题12分）已知球面上三点A、B、C，且AB=18，BC=24，AC=30，球心O到截面ABC的距离为球半径的一半。（1）求球O的表面积；（2）求A、C两点的球面距离。
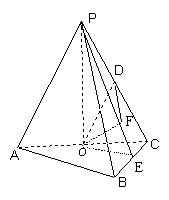
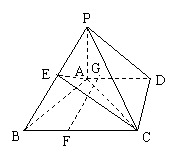19.（本题12分）如图，已知四棱锥P—ABCD中，PA⊥平面ABCD，底面ABCD是直角梯形，∠ADC为直角，，AD∥BC，AB⊥AC，且AB = AC = 2，G为ΔPAC的重心，E为PB的中点，F在线段BC上，且CF = 2FB。（1）求证：FG⊥AC；（2）当二面角P—CD—A多大时，FG⊥平面AEC？
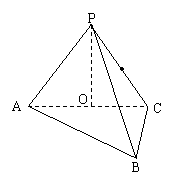20.(本题13分）如图，在三棱锥P－ABC中，AB⊥BC，AB＝BC＝kPA，点O 分别是AC、PC的中点，O P⊥底面ABC．（1）当k＝时，求直线PA与平面PBC所成角的大小；（2） 当k取何值时，O 在平面PBC内的射影恰好为△PBC的重心？
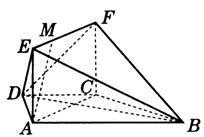21.(本题14分）如图，在梯形ABCD中，
，
，
，平面
平面ABCD，四边形
是矩形，
，点在线段
上.（1）求证：
平面；（2）当
为何值时，
平面
？证明你结论；（3）求二面角
的大小。
参考答案
一、选择题
| 题 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答 案 | B | C | C | C | C | D | B | B | B | C |
二、填空题
11. 不确定
12.
13.
14.
或
或
15.①③
三、解答题
16.（1）
；（2）
17.（1）120； （2）78； （3）48； （4）72；
18.由题易知：
，故
，所以：
（1）
（2）
，
19.（1）连
，并延长交
于，连
，故
，
（2）要使FG⊥平面AEC，只需
即可。设
和的交点为
，故为
的重心。设
，所以：
，
，所以：
，
即
，故：
；所以：
，即二面角P—CD—A为
。
20.（1）（Ｉ）取
的中点Ｄ,
Ｏ、Ｄ分别为
、的中点.
又
平面
.
平面.
,
又
平面
.
取
中点Ｅ，连结
,则
平面
.
作
于F,连结
,则
平面
,
是与平面所成的角.
又
与平面所成角的大小等于.
在
中，
与平面所成的角为
.
（2）由II知，平面，
是在平面内的射影.
是的中点，
若点是
的重心，
则、、三点共线，
直线
在平面内的射影为直线．
，即
．
反之，当时，三棱锥
为正三棱锥，
在平面内的射影为的重心．
21.(1) 由题知梯形ABCD为等腰梯形，又，所以：
。
（2）设
交
于点，连
，要使平面，及要求
，所以四边形
为平行四边形。故
。
（3）取的中点，
的中点，连
，
，
，易知
二面角的平面角。又
，
，
，
所以：
，故二面角为
。