高二数学上学期期末模拟试卷
命题人:李正洋 审核人:张达连
时间:120分钟 分值:160分 使用时间:2008.01
一、填空题
1、样本a1, a2, a3, …, a10的平均数为![]() ,样本b1, b2, b3, …, b20的平均数为
,样本b1, b2, b3, …, b20的平均数为![]() ,则样本a1,a2,a3,…,a10, b1,b2,b3,…,b20的平均数为(用
,则样本a1,a2,a3,…,a10, b1,b2,b3,…,b20的平均数为(用![]() ,
,![]() 表示)
________.
表示)
________.
2、抛物线![]() 的焦点坐标是
_____.
的焦点坐标是
_____.
3、已知条件![]() ,条件
,条件![]() ,则
,则![]() 是
是![]() 的
_______条件.
的
_______条件.
4、为了解1200名学生对学校某项教改试验的意见,打算从中抽取一个容量为30的样本考虑采取系统抽样,则分段的间隔(抽样距)k为 _____.
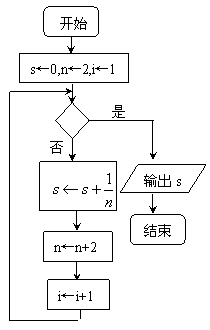 5、以下给出的是计算
5、以下给出的是计算![]() 的值的一个流程
的值的一个流程
图(如图所示),其中判断框内应填入的条件是_______.
6、写出命题:“至少有一个实数![]() , 使
, 使![]() =
=
定 .
7、经过点![]() 且与双曲线
且与双曲线![]() 有共同渐
有共同渐
近线的双曲线方程为 ________.
8、口袋内装有100个大小相同的红球、白球和黑球,其
中有45个红球,从中摸出1个球,摸出白球的概率为
0.23,则摸出黑球的概率为 .
9、(文科班)已知函数![]() ,若
,若
![]() 是
是![]() 的一个极值点,则
的一个极值点,则![]() .
.
(理科班)已知向量![]() 若
若
![]()
![]() 则实数
则实数![]() ______,
______,![]() _______.
_______.
10、已知椭圆![]() 的离心率
的离心率![]() ,则k的值等于________________.
,则k的值等于________________.
11、记定点![]() 与抛物线
与抛物线![]() 上的点P之间的距离为d1,P到抛物线准线L的距
上的点P之间的距离为d1,P到抛物线准线L的距
离为d2,则当d1+d2取最小值时,P点坐标为________________.
12、若双曲线![]() 上一点P到右焦点的距离为8,则P到左准线的距离为________.
上一点P到右焦点的距离为8,则P到左准线的距离为________.
13、分别在区间[1,6]和[2,4]内任取一实数,依次记为m和n,则![]() 的概率为
.
的概率为
.
14、(文科班)已知函数![]() 的图象在点
的图象在点![]() 处的切线与直线
处的切线与直线![]() 平行,则
平行,则![]() .
.
(理科班)若![]() ,
,![]() ,
,![]() 是平面
是平面![]() 内的三点,设平面
内的三点,设平面![]() 的法向
的法向
量![]() ,则
,则![]() ________________.
________________.
二、解答题
15、已知条件![]() :
:![]() ,
,![]() .若
.若![]() 是
是![]() 的充分而不必要条件,求正实数
的充分而不必要条件,求正实数![]() 的取值范围.
的取值范围.
16、已知双曲线过点P![]() ,它的渐近线方程为
,它的渐近线方程为![]()
(1)求双曲线的标准方程;
(2)设F1和F2是这双曲线的左、右焦点,点P在这双曲线上,且PF1·PF2=32,求
∠F1PF2的大小.
17、(文科班)同时掷3个骰子。求:(1)三个骰子的点数都是4的概率; (2)三个骰子的点数和小于5的概率。(3)三个骰子的点数至少有两个相同的概率;
(理科班)已知正方形![]() ,边长为2,正方形内任意一点的选取都是等可能的,任选一点
,边长为2,正方形内任意一点的选取都是等可能的,任选一点![]() ,作
,作![]() 于
于![]() ,
,![]() 于
于![]() ,矩形
,矩形![]() 的面积为
的面积为![]() 。
。
 (1)请建立适当的坐标系,设
(1)请建立适当的坐标系,设![]() ,作出满足
,作出满足![]() 的
的![]() 点的区域,并写出
点的区域,并写出![]() 满足的条件;
满足的条件;
(2)![]() 的概率大于0.5吗?试通过计算说明。
的概率大于0.5吗?试通过计算说明。
18、(文科班)已知曲线![]() 过点P(1,3),且在点P处的切线恰好与直线
过点P(1,3),且在点P处的切线恰好与直线![]() 垂直. 求(Ⅰ) 常数
垂直. 求(Ⅰ) 常数![]() 的值; (Ⅱ)
的值; (Ⅱ)![]() 的单调区间.
的单调区间.
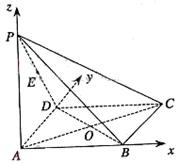
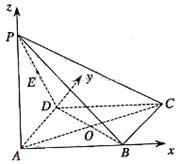
(理科班)如图,在四棱锥![]() 中,底面
中,底面![]() 为矩形,侧棱
为矩形,侧棱![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
(Ⅰ)求直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(Ⅱ)在侧面![]() 内找一点
内找一点![]() ,使
,使![]() 面
面![]() ,并求出点
,并求出点![]() 到
到![]() 和
和![]() 的距离.
的距离.
19、(文科班)设曲线![]() 上的点
上的点![]() ,过
,过![]() 作曲线
作曲线![]() 的切线。
的切线。
(1) 若![]() ,求过点
,求过点![]() 的切线方程;
的切线方程;
(2)设曲线![]() 焦点为
焦点为![]() ,切线与
,切线与![]() 轴交于A,求证:
轴交于A,求证:![]() 是等腰三角形。
是等腰三角形。
(理科班)在棱长为4的正方体![]() 中,
中,![]() 正方形
正方形![]() 的中心,点
的中心,点![]() 在棱
在棱![]() 上,且
上,且![]() .
.
(1)求直线![]() 与平面
与平面![]() 所成角的余弦值;
所成角的余弦值;
(2)设点![]() 在平面
在平面![]() 上的射影为
上的射影为![]() ,求证:
,求证:![]() ;
;
(3)求点![]() 到平面
到平面![]() 的距离.
的距离.
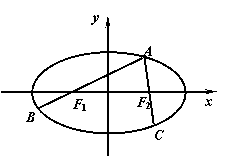 20、如图,A为椭圆
20、如图,A为椭圆![]() 上的一个动点,弦AB、AC分别过焦点F1、F2,当AC垂直于x轴时,恰好有AF1:AF2=3:1.
上的一个动点,弦AB、AC分别过焦点F1、F2,当AC垂直于x轴时,恰好有AF1:AF2=3:1.
(Ⅰ) 求椭圆的离心率;
(Ⅱ) 设![]() .
.
①当A点恰为椭圆短轴的一个端点时,求![]() 的值;
的值;
②当A点为该椭圆上的一个动点时,试判断![]() 是否
是否
为定值?若是,请证明;若不是,请说明理由.
东沟中学高二数学期末模拟试卷参考答案
一、填空题(14*5=70分)
1、![]() 2、
2、![]() 3、充分不必要
4、40
5、
3、充分不必要
4、40
5、![]()
6、![]() 7、
7、![]() 8、0.32 9、(文)2;(理)
8、0.32 9、(文)2;(理)![]()
10、![]() 11、
11、![]() 12、
12、![]() 13、
13、![]() 14、(文)
14、(文)![]() ;(理)
;(理)![]()
二、解答题
15、![]()
16、解(1)由渐近线方程知双曲线中心在原点,且渐近线上横坐标为![]() 的点
的点![]() 的纵坐
的纵坐
标绝对值为![]() ,
,![]() ∴双曲线的焦点在
∴双曲线的焦点在![]() 轴上,设方程
轴上,设方程![]()
∵双曲线过点![]() ① 又
① 又![]() ②
②
由①②得![]() ,∴所求的双曲线方程为
,∴所求的双曲线方程为![]() …………6分
…………6分
(2)证PF1=d1,PF2=d2,则d1·d2=32
又由双曲线的几何性质知d1-d2=
![]() 即有
即有![]() ………………10分
………………10分
又F![]()
△PF![]() ………………………………12分
………………………………12分
17、解:(文)(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
(理)(1)以![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为坐标原点建立直角坐标系。
为坐标原点建立直角坐标系。![]() 满足:
满足:![]() 所围成的区域。
所围成的区域。
(2)阴影部分面积![]()
使得![]() 的概率
的概率![]()
18、解(文)(Ⅰ)据题意![]() ,所以
,所以![]() (1)
(1)
![]() ,
,
又曲线在点P处的切线的斜率为![]() ,
,
∴![]() ,即
,即![]() (2)由(1)(2)解得
(2)由(1)(2)解得![]() .
.
(Ⅱ)![]() . ∴当
. ∴当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .∴
.∴![]() 的单调区间为
的单调区间为![]() ,在区间
,在区间![]() 上是增函数,在区间
上是增函数,在区间![]() 上是减函数.
上是减函数.
(理)(Ⅰ)建立如图所示的空间直角坐标系,
|
![]() 、
、![]() 、
、![]() 、
、
![]() 、
、![]() ,
,
从而![]()
设![]() 的夹角为
的夹角为![]() ,则
,则
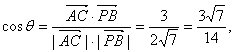 ∴
∴![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() .
.
(Ⅱ)由于![]() 点在侧面
点在侧面![]() 内,故可设
内,故可设![]() 点坐标为
点坐标为![]() ,则
,则
![]() ,由
,由![]() 面
面![]() 可得,
可得,
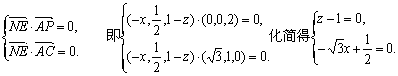 ∴
∴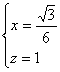
即![]() 点的坐标为
点的坐标为![]() ,从而
,从而![]() 点到
点到![]() 和
和![]() 的距离分别为
的距离分别为![]() .
.
19、解:(文)(1)![]() ,切线方程为
,切线方程为![]() ,即
,即![]()
(2)![]() 处切线方程:
处切线方程:![]() ,将
,将![]() 代入,
代入,
得![]() ,焦点
,焦点![]() 坐标
坐标![]() ,
,
![]() ,又
,又![]() ,
,![]() ,即
,即![]() 是等腰三角形。
是等腰三角形。
(理)![]() 复习题第13题
复习题第13题
20、解(Ⅰ)设![]() ,则
,则![]() .由题设及椭圆定义得
.由题设及椭圆定义得![]() ,
,
消去![]() 得
得![]() ,所以离心率
,所以离心率![]() .
.
(Ⅱ) 由(1)知,![]() ,所以椭圆方程可化为
,所以椭圆方程可化为 ![]() .
.
①当A点恰为椭圆短轴的一个端点时,![]() ,直线
,直线![]() 的方程为
的方程为![]() .
.
由![]() 得
得 ![]() ,解得
,解得![]() ,
,
∴ 点![]() 的坐标为
的坐标为![]() .
.
又![]() ,所以
,所以![]() ,
,![]() ,所以
,所以![]() ,
,![]() .
.
②当A点为该椭圆上的一个动点时,![]() 为定值6.
为定值6.
证明 设![]() ,
,![]() ,则
,则![]() .
.
若![]() 为椭圆的长轴端点,则
为椭圆的长轴端点,则![]() 或
或![]() ,
,
所以![]() .
.
若![]() 为椭圆上异于长轴端点的任意一点,则由
为椭圆上异于长轴端点的任意一点,则由![]() 得,
得,
![]() ,所以
,所以![]() .
.
又直线![]() 的方程为
的方程为![]() ,所以由
,所以由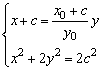 得
得
![]() .
.![]() ,
,
∴![]() .
.
由韦达定理得 ![]() ,所以
,所以![]() . 同理
. 同理 ![]() .
.
∴![]() .
.
综上证得,当A点为该椭圆上的一个动点时,![]() 为定值6.
为定值6.