高二数学上学期期末统考试题及答案(理) 2008年1月
一、选择题:(本大题共12小题,每小题5分,共60分。在各题所给出的四个选项中,有且只有一个是正确的,请将正确选项的代号填在答题卡上)
1.已知命题![]() 是 (
)
是 (
)
A.![]() B.
B.![]()
C.![]() D.
D.![]()
2. 椭圆![]() 的距离是 ( )
的距离是 ( )
A.![]() B.
B.![]() C.1 D.
C.1 D.![]()
3.条件P:“直线l在y轴上的截距是在x轴上截距的两倍”;条件q:“直l的斜率为-
则p是q的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.非充分也非必要条件
4. 已知x>2,则![]() 有
有
A 最大值1.25 B 最小值
5.在△ABC中,边a、b、c所对角分别为A、B、C,且![]() ,则△ABC的形状为 ( )
,则△ABC的形状为 ( )
A.等边三角形 B.有一个角为30°的直角三角形
C.等腰直角三角形 D.有一个角为30°的等腰三角形
6. 若互不相等的实数a、b、c成等差数列, c、a、b成等比数列,且a+3b+c=10, 则a等于
A.4
B.
7.已知F1、F2的椭圆![]() 的焦点,M为椭圆上一点,MF1垂直于x轴,
的焦点,M为椭圆上一点,MF1垂直于x轴,
且![]() 则椭圆的离心率为 (
)
则椭圆的离心率为 (
)
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
8. 已知等差数列{an}中, Sn是它的前n项和,若S16>0, S17<0, 则当Sn取最大值时,n的值为
A.16 B.
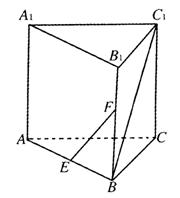
9.
|
中,AA1⊥底面ABC,AB=BC=AA1,
∠ABC=90°。点E、F分别是棱AB、
BB1的中点,则直线EF和BC1所成
的角是 ( )
A.45°
B.60°
C.90°
D.120°
10.
|
A.2 B.![]() D.
D.![]()
11. 已知![]() 的最小值为 (
)
的最小值为 (
)
A.6 B.
12. 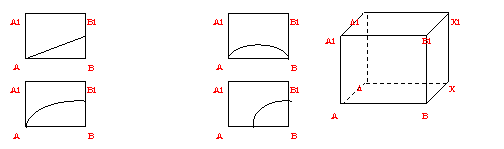 如图所示,在正方体
如图所示,在正方体![]() 的侧面
的侧面![]() 内有一动点
内有一动点![]() 到直线
到直线![]() 和直线
和直线![]() 的距离相等,则动点
的距离相等,则动点![]() 所在曲线形状为
所在曲线形状为
(A) (B)
(C) (D)
第Ⅱ卷(非选择题 共90分)
二 填空:(每小题4分,共16分,把答案填在题中横线上)
13. 命题“若![]() ,则
,则![]() ”的逆否命题为
。
”的逆否命题为
。
13.若![]() , 则
, 则![]()
14. 设等差数列![]() 的公差
的公差![]() 0,又
0,又![]() 成等比数列,则
成等比数列,则![]() 。
。
14.![]()
15. 已知实数x、y满足条件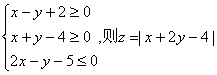 的最大值为
.
的最大值为
.
15.21
|
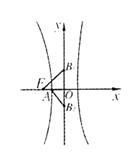
16.如图,双曲线C的中心在原点,虚轴两端点
分别为B1、B2,左顶点和左焦点分别为A、F,
若![]() ,则双曲线C的离心率为
,则双曲线C的离心率为
.
16.![]()
三、 解答题:(本大题6小题,共74分,解答应写出文字说明,证明过程或演算步骤)
17. (本小题满分12分)
在⊿ABC中,已知![]() .
.
(1)求出角C和A ;
(2)求⊿ABC的面积S.
17.(1)![]() ,
,![]() ………………………………………………3分
………………………………………………3分
![]() ………6分
………6分
(2)S=0.5bcsinA=![]() ……………………………………………………12分
……………………………………………………12分
18. (本小题满分12分)
已知一个数列![]() 的各项是1或2.首项为1,且在第
的各项是1或2.首项为1,且在第![]() 个1和第
个1和第![]() 个1之间有
个1之间有![]() 个2,即1,2,1,2,2,2,1,2,2,2,2,2,1,….记数列的前
个2,即1,2,1,2,2,2,1,2,2,2,2,2,1,….记数列的前![]() 项的和为
项的和为![]() .
.
(1)试问第![]() 个1为该数列的第几项?
个1为该数列的第几项?
(2)求![]() ;
;
(3)求![]() ;
;
18.解:记(1,2)为第1对,共1+1=2项;(1,2,2,2)为第2对,共1+(2×2-1)=4项;![]() 为第k对,共1+(2k-1)=2k项,……
为第k对,共1+(2k-1)=2k项,……
故前k对共有项数为![]() ………………………………………3分
………………………………………3分
(Ⅰ)第![]() 个1所在的项为前
个1所在的项为前![]() 对所在全部项的后1项,
对所在全部项的后1项,
即为![]() ,即
,即![]() ……………………6分
……………………6分
(Ⅱ)因44×45=1980,45×46=2070,故第2006项在第45对内,从而![]()
……………………………9分
(Ⅲ)由(Ⅱ)可知,前2006项中共有45个1,其余1961个数均为2,于是![]() =45+2×1961=3967. …………………………12分
=45+2×1961=3967. …………………………12分
19. (本小题满分12分)
日照市某商场为使销售空调和冰箱获得的总利润达到最大,对即将出售的空调和冰箱相关数据进行调查,得出下表:
| 资金 | 每台空调或冰箱所需资金(百元) | 月资金供应数量 (百元) | |
| 空调 | 冰箱 | ||
| 成本 | 30 | 20 | 300 |
| 工人工资 | 5 | 10 | 110 |
| 每台利润 | 6 | 8 |
|
问:该商场怎样确定空调或冰箱的月供应量,才能使总利润最大?
19.设空调和冰箱的月供应量分别为![]() 台,月总利润为
台,月总利润为![]() 百元
百元
则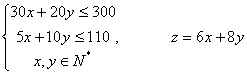 ………………………………………3分
………………………………………3分
作出可行域……………………………………………………………………………6分
![]() ,纵截距为
,纵截距为![]() ,斜率为k=
,斜率为k=![]() ,满足
,满足![]()
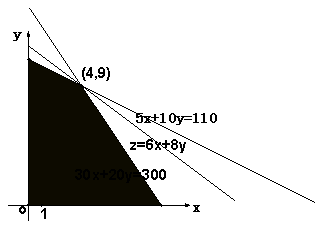 欲
欲![]() 最大,必
最大,必![]() 最大,此时,直线
最大,此时,直线![]() 必过图形
必过图形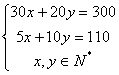
的一个交点(4,9),![]() 分别为4,9
分别为4,9
∴空调和冰箱的月供应量分别为4、9台时,月总利润为最大.…………… ……12分
20. (本小题满分12分)
已知数列![]()
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)若![]() 求数列
求数列![]() 的前n项和
的前n项和![]()
20.解:
(Ⅰ)![]() ……………………2分
……………………2分
![]() …………………………………………………………3分
…………………………………………………………3分
又![]() ,
,
![]() ………………………………4分
………………………………4分
![]() ……………………5分
……………………5分
(Ⅱ)![]()
![]() …………………………7分
…………………………7分
![]() ……………………8分
……………………8分
![]() ……………………9分
……………………9分
![]()
![]() ………………………………………………11分
………………………………………………11分
![]() ……………………………………12分
……………………………………12分
21. (本小题满分12分)
如图,已知ABCD是正方形,PD⊥平面ABCD,PD=AD.
(1)求二面角A-PB-D的大小;
(2)在线段PB上是否存在一点E,使PC⊥平面ADE?若存在,确定E点的位置,若不存在,说明理由.
21.解:(1)以向量![]() 为正交基底,建立空间直角坐标系.
为正交基底,建立空间直角坐标系.
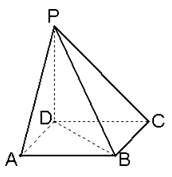 联结AC,交BD于点O,取PA中点G,联结DG.
联结AC,交BD于点O,取PA中点G,联结DG.
∵ABCD是正方形,∴AC⊥DB.
又PD⊥平面ABCD,AC![]() 平面ABCD,
平面ABCD,
∴AC⊥PD, ∴AC⊥平面PBD.
∵PD⊥平面ABCD,AB⊥AD,∴PA⊥AB.
∴AB⊥平面PAD.
∵PD=AD,G为PA中点, ∴GD⊥平面PAB.
故向量![]() 分别是平面PBD与平面PAB的法向量.
分别是平面PBD与平面PAB的法向量.
令PD=AD=2,则A(2,0,0),C(0,2,0),∴![]() =(-2,2,0).
=(-2,2,0).
∵P(0,0,2),A(2,0,0), ∴G(1,0,1),∴![]() =(1,0,1).
=(1,0,1).
∴向量![]() 的夹角余弦为
的夹角余弦为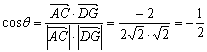 ,
,
∴![]() ,∴二面角A-PB-D的大小为
,∴二面角A-PB-D的大小为![]() .
.
(2) ∵PD⊥平面ABCD,AD⊥CD,∴AD⊥PC.
设E是线段PB上的一点,令![]() .
.
∴![]() (-2,0,2),
(-2,0,2),![]() (2,2,-2),
(2,2,-2),![]() (0,2,-2).∴
(0,2,-2).∴![]() .
.
∴![]() .
.
令![]() 2
2![]() (
(![]() -
-![]() )=0,得
)=0,得![]() .
.
∴当![]() ,即点E是线段PB中点时,有AE⊥PC.
,即点E是线段PB中点时,有AE⊥PC.
又∵PD⊥平面ABCD,AD⊥CD,∴AD⊥PC. ∴当点E是线段PB中点时,有PC⊥平面ADE.
22. (本小题满分14分)
已知定点F(1,0),动点P在y轴上运动,过点P做PM交x轴于点M,并延长MP到点N,且![]()
(Ⅰ)求点N的轨迹方程;
(Ⅱ)直线l与点N的轨迹交于A、B不同两点,若![]() ,且
,且![]() ,求直线l的斜率k的取值范围.
,求直线l的斜率k的取值范围.
22.解:
(Ⅰ)由于![]()
则P为MN的中心,
设N(x,y),则M(-x,0),P(0,![]() ),……………………2分
),……………………2分
由![]()
得![]()
![]()
![]()
所以点N的轨迹方程为![]() …………………………5分
…………………………5分
(Ⅱ)设直线l的方程是![]()
与![]() :
:
![]() ……………………6分
……………………6分
设![]()
则:![]()
![]()
![]() ……………………7分
……………………7分
由![]()
![]()
即![]()
![]() …………………………9分
…………………………9分
由于直线与N的轨迹交于不同的两点,
则![]()
把![]()
![]()
而![]()
![]()
![]()
![]()
![]()
又因为![]()
![]()
解得![]()
综上可知k的取值范围是![]() .……………………14分
.……………………14分