高二数学上学期期末考试试卷

高二数学上学期期末考试试卷

高二年级数学试题（理）

命题人：江国新　　　　　 

一、选择题（5分×10=50分）

1．已知α，β，γ是两两相交的三个平面，则α∩β∩γ等于

A．一个点　　　　　　　　　　　  B．一条直线　　　

C．　　　　　　　　　　　　　  D．以上三种情况均有可能

2．空间四边形ABCD中，AB=CD，AB与CD成30°角，E、F分别为BC、AD的中点，则EF和AB所成角为

A．15°　　　　  B．75°　　　　 C．15°或75°　　  D．30°

3．给出以下四个命题

①过空间一点有且只有一个平面与两条异面直线都平行

②过两条异面直线中的一条有且只有一个平面与另一条直线平行

③过两条异面直线中的一条有且只有一个平面与另一条直线垂直

④与两条异面直线都相交的两条直线是异面直线

其中真命题的个数为

A．4　　　　　　 B．3 　　　　　　C．2　　　　　  D．1

4．已知A(1,－2,11)，B(4,2,3)，C(6,－1,4)，则△ABC是

A．钝角三角形　　B．锐角三角形　　 C．直角三角形　　D．等腰三角形

5．关于直线m，n与平面α、β，有下列四个命题：

①若m//α，n//β且α//β，则m//n

②若m⊥α，n⊥β且α⊥β，则m⊥n

③若m⊥α，n//β且α//β，则m⊥n

④若m//α，n⊥β且α⊥β，则n//m

其中真命题的个数为

A．1　　　　　　  B．2 　　　　　　C．3　　　　　　 D．4

6．若，且的夹角为锐角，则λ的取值范围为

A．－1<λ<4　　　　　　　　　　　  B．－1<λ<

C．<λ<4　　　　　　　　　　　　 D．－1<λ<或<λ<4

7．双曲线C：与直线l：mx+ny+t=0的公共点个数可能为

①0个　　　 ②1个　　　　 ③2个　　　 ④3个　　 ⑤4个

其中命题正确的个数为

A．2　　　　　  B．3 　　　　　C．4　　　　　 D．5

8．在正方体ABCD—A₁B₁C₁D₁中，M为DD₁的中点，O为ABCD的中心，P为棱A₁B₁上的任一点，则直线OP与AM所成角为

A．30°　　　　 B．45°　　　　C．60°　　　　D．90°

9．对于四面体ABCD，给出下列四个命题

①若AB=AC，DB=DC，则AD=BC　　 ②若AB=CD，AC=BD，则BC⊥AD

③若AB⊥AC，BD⊥CD，则BC⊥AD　④若AB⊥CD，BD⊥AC，则BC⊥AD

其中真命题的个数为

A．1　　　　　　 B．2 　　　　　 C．3　　　　　 D．4

10．长方体ABCD—A₁B₁C₁D₁中，P为底面ABCD内的一动点，P到点B的距离与P到直线DD₁的距离之比为e(0<e<1)，则点P的轨迹是

A．椭圆的一部分　　　　　　　　  B．双曲线的一部分

C．圆的一部分　　　　　　　　　  D．线段

二、填空题（5分×5=25分）

11．过点P(1,2)且在两坐标轴上的横纵截距互为相反数的直线方程为____________.

12．已知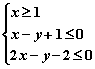，则(x－6)²+y²的最小值为_______________.

13．已知，则方向上的正射影为_______________.

14．设矩形ABCD(AB>AD)的周长为12，把它关于AC折起来，AB折过去后，交DC于点P，则△ADP的最大面积为______________.

15．已知四面体PABC中，PA=3，PB=4，PC=5，∠APB=∠BPC=∠APC=60°，则AP与平面PBC所成角为_______________，=____________.

高二数学上学期期末考试试卷

高二年级数学试题（理）答题卷

一、选择题答题卡

题号	1	2	3	4	5	6	7	8	9	10
答案

二、填空题答题卡

11．_________________　　　　　　　　　 12．________________

13．________________　　　　　　　　　  14．________________

15．________________　　___________________　　

三、解答题

16．（本小题12分）已知空间四边形OABC中，OA=OB，CA=CB，E、F分别为OA、OB的中点

（1）若G、H分别为BC、AC的中点，求证：四边形EFGH是矩形；

（2）若G、H分别为BC、AC上的点，且，求证三条直线FG、HE、OC交于一点.

17．（本小题12分）已知关于x的不等式

（1）若不等式的解集为R，求实数a的取值范围；

（2）是否存在实数a使不等式的解集为(－1,1)？

18．（本小题12分）在矩形ABCD中，AB=，BC=1，沿对角线BD将△BCD折起，使点C移到点，且点在平面ABD上的射影O恰在AB上

（1）求证：B⊥平面AD；

（2）求直线AB与平面BD所成角的大小.

19．（本小题12分）已知圆C的方程为x²+y²－2(t+3)x+2(1－4t²)y+16t⁴+9=0(t∈R)

（1）求圆C的面积的取值范围；

（2）过点P(3,4t²)的直线l与圆C的公共点的个数为0或1或2，求t的取值范围.

20．（本小题13分）已知矩形ABCD中，AB=a，BC=2，PA⊥平面ABCD，且PA=1

（1）若M、N分别为BC、PD的中点，求证：MN//平面PAB；

（2）若BC边上有且只有一个点Q，使PQ⊥DQ，试求异面直线QN与CD所成的角.

21．（本小题14分）求出一个数学问题的正确结论后，将其作为条件之一，提出与原来问题有关的新问题，我们把它称为原来问题的一个“逆向”问题. 例如：原来问题是“在平面直角坐标系xOy中，求点P(2,1)到直线3x+4y=0的距离”，求出距离2后，它的一个“逆向”问题可以是“求到直线3x+4y=0的距离为2的点的轨迹方程”；也可以是“若点P(2,1)到直线l：ax+by=0的距离为2，求直线l的方程.”

　 试给出问题“过抛物线C：y²=2px(p>0)焦点F的一条直线与抛物线C交于两点P、Q，经过点P和抛物线顶点的直线交准线于点M，求证：MQ//x轴”的一个有意义的“逆向”问题，并解答你所给出的“逆向”问题.