高二数学上学期期末考试试卷
高 二 数 学（文）
时间：120分钟 分值：150分 命题人:天门中学 彭文浩
一. 选择题：（本题共10小题，每小题5分，共50分）
1. 若
，
，则下列不等式成立的是（ ）
A. 
B.
C. 
D.
2. 圆心在y轴上，半径为5，且与直线
相切的圆的方程为（ ）
A. 
B.
C. 或
D. 
或
3.已知圆x2+y2=4关于直线l对称的圆的方程为(x+3)2+(y–3)2=4，则直线l的方程为( )
A 、y= x+2 B y= x+
4. 若椭圆
过点
，则其焦距为（ ）
A. 
B.
C.
D.
5. 已知直线l的倾斜角
满足
，则l的斜率为（ ）
A. 
B.
C.
或
D.
或
6. 若抛物线的顶点在原点，焦点是双曲线
的顶点，则抛物线的方程是（ ）
A. 
B.
C. 
D.
7. 若不等式
，则
的取值范围是（ ）
A. 
B.
C.
D.
8. 已知直线
，下列说法正确的是（ ）
A. 
到
的角是
B. 到的角是
C. 到的角是 D. 与的夹角是
9. 已知双曲线
，若椭圆N以M的焦点为顶点，以M的顶点为焦点，则椭圆N的准线方程是（ ）
A. 
B.
C.
D.
10我国发射的“神舟六号” 宇宙飞船运行的轨道是以地球中心为一焦点的椭圆，测得近地点距地面m千米，远地点距地面n千米，地球半径为r千米，则该飞船运行轨道的短轴长为( )
A、
千米 B、
千米 C、
千米 D、
千米
二. 填空题（本题共5小题，每小题5分，共25分）
11. 直线2x－4y+5=0与5x+3y+7=0的夹角的正切值为 . 翰林汇
12．设PQ是抛物线 y2 = 2px (p>0)上过焦点F的一条弦，l是抛物线的准线，则以PQ为直径的圆与准线的位置关系是 .
13．已知C：(x+1)2+( y+a)2=4及直线l：3x－4y+3=0，当直线l被C截得的弦长为2时，则a= .
14．已知椭圆(a>b>0)与双曲线(m>0，n>0)有相同的焦点(－c，0)和(c，0)． 若c是a与m的等比中项，n2是m2与c2的等差中项，则椭圆的离心率等于 .
15、已知
分别为双曲线的左、右焦点，P是为双曲线
左支上的一点，若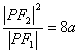
，则双曲线的离心率的取值范围是
三. 解答题（本题共75分）
16．（本题12分）已知x＞0，y＞0，且2x＋y＝3，求＋的最小值．
17.．（本小题满分12分）某运输公司接受了向地区每天至少运送180吨物资的任务，该公司有8辆载重为6吨的A型卡车与4辆载重为10吨的B型卡车，有10名驾驶员，每辆卡车每天往返的次数为A型卡车4次，B型卡车3次，每辆卡车每天往返的成本费用为A型卡车320元，B型卡车504元，请你给该公司调配车辆，使公司所花的成本费用最低.
18.（本题满分12分）
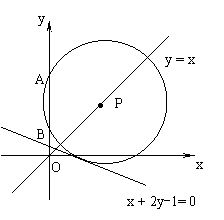如图所示，圆心P 在直线
上，且与直线
相切的圆，截
轴的上半轴所得的弦
长为2，求此圆的方程．
19. 已知双曲线 - =1(a>0,b>0)的左、右焦点分别为F1、F2，点P在双曲线的右支上，且PF1=3PF2.
(1)求离心率的取值范围，并写出此时双曲线的渐近线方程.
(2)若点P的坐标为(，)时，
=0，求双曲线方程.
20. （本题满分13分） 已知抛物线y2=2px ，在x轴上是否存在一点M，使过M的任意直线l（x轴除外），与抛物线交于A,B两点，且总有∠AOB=900（O为坐标原点）。若存在，求出点M的坐标；若不存在，请说明理由。
21.．（本题14分）如图，
、
为椭圆
的左右焦点，P为椭圆上一点，且位于
轴上方，过点P作x轴的平行线交椭圆右准线于点M，连接
，
（1）若存在点P，使
为平行四边形，求椭圆的离心率e的取值范围；
（2）若存在点P，使为菱形；
①求椭圆的离心率；
②设
、
，
求证：以
为直径的圆经过点B．
第一学期期末试卷
高二数学（文科）答案
一. 选择题（本题共50分，每小题5分）
1. B 2. c 3.B 4. C 5. D 6. D
7. A 8. C 9. B 10. A
二. 填空题（本题共25分，每小题5分）
11. 13 翰林汇 12．相切 13．± 14． 15. 
三. 解答题（本题共75分，）
16..（本题满分12分）
解 ：＋＝＝≥＝，……10分
当且仅当4－y＝y＋2时，即y＝1时取等号．……12分
17．设每天调出A型卡车x辆,B型卡车y辆,公司所花成本为z元,则据题设可得如下约束条件:
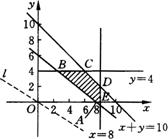
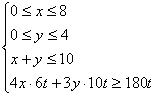即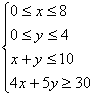
目标函数为
（x和y均为整数),作出可行域如下图中的阴影部分,作直线
,把直线
向右上方作平行移动,经过点
时
取最小值,但
不是整数,所以(,0)不是最优解.继续平移直线,直线
上的整点(5,2)应是首先经过的,使取最小值,
.
答:每天调出A型卡车5辆,B型卡车2辆,公司所花成本最低.
18. （本题满分12分）
解：∵圆心P在直线y = x上，∴可设P的坐标为（k，k），（k>0）……１分
作PQ⊥AB于Q，连接AP，在Rt△APQ中，AQ=1，AP=r，PQ=k
∴r=
…………………………３分
又r=点P到直线x + 2y-1= 0的距离
∴
………………………６分
整理，得
…………………………………………７分
解得，k=2或
（舍去） ………………………９分
∵所求圆的半径为
=
………………………１１分
∴所求圆的方程为：
…………………１２分
19. (1)∵PF1－PF2=
∵P在双曲线的右支上，∴x0≥a，即≥a,解得1<e≤2, ∴e的最大值为2，此时 =4，b=a,∴渐近线方程为y=±x.
（2）设
，
=(－c－x0，－y0)，
=(c－x0，－y0)，又
∴=0，∴－(c2－x02)+y02=0，∴c2=x02+y02=10. ①
又P点在双曲线上， ∴
， ②
∴联立①②解得
.
∴双曲线方程为 - =1.
20.. （本题满分13分）
解：存在满足条件的点M ……2分
设点
（1）当斜率k不存在时，则
，由
，知
……4分
……5分
，即M（2p，0） ……7分
（2）当斜率k存在时，则L的方程为
由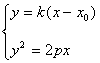
得
即
……9分
又由，知 ……11分
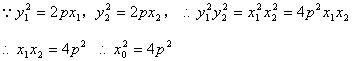
，即M（2p，0） ……13分
由（1）（2）可知满足条件的点M的坐标为（2p，0） ……14分
21．（14分）
（1）设
，则
，∵
，
∴
，
由
；
（2）①
，
，∵
，∴
；
②以为直径的圆方程为
，
下证满足方程，即
…（＊），
∵
，∴
，∴
，∴（＊）成立，
∴以为直径的圆经过点B．