高二数学第一学期期中试卷
命题人：杭丽华 审核人：汪秀松
注意事项：
本试卷共21小题，总分100分，考试时间为120分钟．
一、填空题：本大题共10小题，每小题3分，共30分．
1．命题“对任意的
”的否定是
▲ ．
2．某校有学生2000人，其中高三学生500人．为了解学生的身体素质情况，采用按年级分层抽样的方法，从该校学生中抽取一个200人的样本．则样
本中高三学生的人数为 ▲ ．
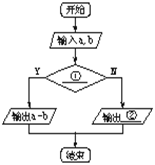
3．根据题意，完成流程图填空：
输入两个数，输出这两个数差的绝对值．
（1） ▲ ；（2） ▲ ．
4．命题“斜率相等的两条直线平行”的逆否命题是 ▲
命题（填“真”或“假”）．
5．连续抛掷一颗骰子2次，则两次掷出的点数之和为4的
概率为 ▲ ． 第3题图
6．已知椭圆的长半轴长为4，焦点坐标是
，则此椭圆的方程为 ▲ ．
7．在等腰直角三角形
的斜边
上任取一点
，则
的概率为 ▲ ．
8．与椭圆
有公共焦点，且离心率为
的双曲线的方程为 ▲ ．
9．一只蚂蚁在边长为3的正方形区域内随机地爬行,则其恰在离四个顶点距离都大于1的
地方的概率 ▲ ．
10．已知双曲线
的左、右焦点分别为
，
，
是准线上一点，且
，
，则双曲线的离心率为 ▲ ．
二、选择题：本大题共6小题，每小题3分，共18分．
11．命题甲“
”，命题乙“
”，那么甲是乙的
（
）
A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件
12．甲、乙两棉农，统计连续五年的单位面积产量（千克/亩）如下表：
| 棉农甲 | 68 | 72 | 70 | 69 | 71 |
| 棉农乙 | 69 | 71 | 68 | 68 | 69 |
则单位面积平均产量较高与产量较稳定的分别是 （ ）
A．甲、甲 B．甲、乙 C．乙、甲 D．乙、乙
13．下面的流程图是循环结构的是 （ ）
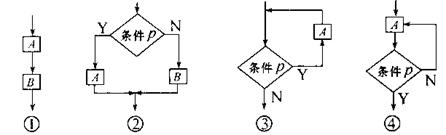
A．①② B．②③ C．③④ D．②④
14．已知
的顶点
在椭圆
上，顶点
是椭圆的一个焦点，且椭圆的另外一个焦点在
边上，则的周长是
（ ）
A．
B．
D．12
15．右面的伪代码输出的结果S为 （ ）
A．17 B．19
C．21 D．23
16．若椭圆
的离心率
，右焦点
，方程
的两个实根分别为
和
，则点
（ ）
A．必在圆
内 B．必在圆上
C．必在圆外
D．以上三种情形都有可能
三、解答题：本大题共5小题，共52分．
17．（本小题满分10分）
袋中有2个白球，3个黑球，从中任意摸出2个，求下列事件发生的概率：
（1）摸出1个或2个黑球；
（2）至少摸出1个白球；
| 分组 | 频数 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 合计 |
|
18．（本小题满分10分）
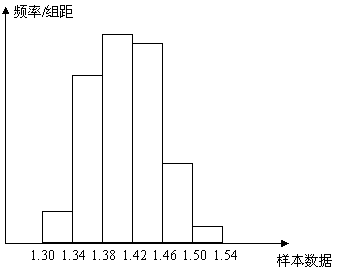
在生产过程中，测得纤维产品的纤度（表示纤维粗细的
一种量）共有100个数据，将数据分组如右表：
（1）在答题卡上完成频率分布表，并画出频率分布
直方图；
（2）估计纤度落在
中的概率和纤度小于
的概率．
19．（本小题满分10分）
（1）已知椭圆中心在原点，焦点在
轴，长轴长为短轴长的3倍，且过点
，求此椭圆的方程；
（2）求与双曲线
有公共渐近线，且焦距为8的双曲线的方程．
20．（本小题满分10分）设计一个算法，求
的值，并画出程序框图．
21．（本小题满分12分）已知双曲线的中心在原点，焦点
在坐标轴上，离心率为
，且过点
．
（1）求双曲线方程；
（2）若点
在双曲线上，求证：
；
（3）求
的面积．
南京大学附属中学2007～2008年度第一学期高二
数学期中试卷参考答案
2007．11．12
说明：
1．本解答仅给出了一种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内容对照评分标准制订相应的评分细则．
2．评阅试卷，应坚持每题评阅到底，不要因为考生的解答中出现错误而中断对该题的评阅，当考生的解答在某一步出现错误时，如果后继部分解答未改变该题的内容和难度，可视影响的程度决定后继部分的给分，但不得超过该部分正确解答应得分数的一半；如果后继部分的解答有较严重的错误，就不再给分．
3．解答右端所注分数，表示考生正确做到这一步应得的累加分数．
4．给分或扣分均以1分为单位，选择题和填空题不给中间分．
一、填空题：每小题3分，满分30分．
1．
2．50
3．
，
4．真
5．
6．
7．
8．
9．
10．
二、选择题：每小题3分，满分18分．
| 题号 | 11 | 12 | 13 | 14 | 15 | 16 |
| 答案 | B | B | C | D | A | A |
三、解答题：本大题5小题，满分52分．
17．解：从5个球中任意摸出2个共有10种不同的结果．记从5个球中任取2个，其中恰有1个黑球为事件
，恰有2个黑球为事件
，恰有1个黑球或恰有2个黑球为事件，至少1个白球为事件
．则
（1）摸出1个或2个黑球的概率
；
或者
…………5分
（2）至少摸出1个白球的概率
． …………10分
18．解：（1）
| 分组 | 频数 |
|
|
| 4 |
|
|
| 25 |
|
|
| 30 |
|
|
| 29 |
|
|
| 10 |
|
|
| 2 |
|
| 合计 | 100 |
|
频率
…………5分
（2）纤度落在
中的概率约为
，
纤度小于的概率约为
．
…………10分
 |
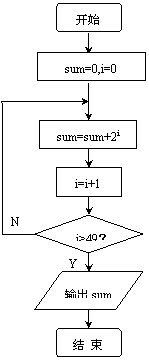19．解：
（1）
；
…………5分
（2）
．
…………10分
20．解：算法步骤：
第一步：sum=0；
第二步：i=0；
第三步：sum=sum+2i；
第四步：i=i+1；
第五步：判断i是否大于49，若成立，则输出sum，结束；
否则返回第三步重新执行． …………5分
程序框图： …………10分
21．解：
（1）由题意，可设双曲线方程为
，又双曲线过点，解得
∴ 双曲线方程为
；
…………4分
（2）由（1）可知，
，
， ∴ 
，
∴ 
，
， ∴ 
，
又点在双曲线上， ∴ 
，
∴ 
， 即；
…………8分
（3）
∴ 的面积为6．
…………12分