高二级数学科第二学期期中考试(理)试卷
考试时间:120分钟 满分:150分 命题教师:ZXL
参考公式
![]()
一. 选择题(每题5分,共40分,每小题答案唯一)
1.在复平面内,复数![]() 对应的点位于( )
对应的点位于( )
(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限
2.函数![]() 的递增区间是( )
的递增区间是( )
(A) ![]() (B)
(B)
![]() (C)
(C) ![]() (D)
(D) ![]()
3.若![]() ,则
,则![]() 的值为( )
的值为( )
(A) 0 (B) 15 (C) 16 (D) 17
4.异面直线![]() 、
、![]() ,
,![]() 上有5个不同点,
上有5个不同点,![]() 上有4个不同点,这9个点一共可组成直线的条数为( )
上有4个不同点,这9个点一共可组成直线的条数为( )
(A) 9 (B) 10 (C) 20 (D) 22
5.用数学归纳法证明![]() 从“k到k+
从“k到k+
(A)![]() (B)
(B) ![]() (C)
(C)![]() (D)
(D) ![]()
6.有4名男生3名女生排成一排,若3名女生中有2名站在一起,但3名女生不能全排在一起,则不同的排法种数有( )
(A) 2880 (B)3080 (C)3200 (D) 3600
7.12名同学分别到三个企业进行社会调查,若每个企业4人,则不同的分配方案共有( )种。
(A)
![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
8.已知![]() 若当
若当![]() 时,
时,![]() 的值都能被9整除.则
的值都能被9整除.则![]() 的最小值为( )
的最小值为( )
(A) 5 (B) 4 (C) 3 (D) 2
二.填空题(每题5分,共30分)
9.实数![]() 满足
满足![]() 则
则![]()
10.利用定积分的几何意义,求![]()
11.用0,1,2,3,4,5六个数字组成无重复数字的三位数,其中能被3整除的有_______个(用数字作答).
12.某餐厅供应客饭,每位顾客可以在餐厅提供的菜肴中任选2荤2素共4种不同的品种,现在餐厅准备了五种不同的荤菜.若要保证每位顾客有200种以上不同选择,则餐厅至少还需要准备不同的素菜品种数为__________.
|
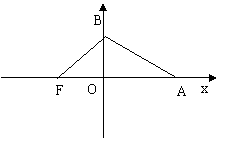
 13.如图所示,椭圆中心在坐标原点,F为左焦点,当FB⊥AB时,其离心率为
13.如图所示,椭圆中心在坐标原点,F为左焦点,当FB⊥AB时,其离心率为
|
14.如图,有一列曲线![]() 是对
是对![]() 进行如下操作得到:将
进行如下操作得到:将![]() 的每条边三等份,以每边中间部分的线段为边,向外作等边三角形,再将中间部分的线段去掉(k=0,1,2,…).则
的每条边三等份,以每边中间部分的线段为边,向外作等边三角形,再将中间部分的线段去掉(k=0,1,2,…).则![]() 边数为________,
边数为________,![]() 边数为________.由此,推测出
边数为________.由此,推测出![]() 的边数为_______.
的边数为_______.
三.解答题:本题共6小题,80分,解答应写出文字说明,证明过程或演算过程.
15.(满分12分)已知![]() 的展开式前3项二项式系数的和为37.
的展开式前3项二项式系数的和为37.
(1)求![]() 的值. (2)这个展开式中是否有常数项?若有,将它求出,若没有,请说明理由.
的值. (2)这个展开式中是否有常数项?若有,将它求出,若没有,请说明理由.
16. (满分14分)(1)计算由曲线![]() 与
与![]() 轴围成的封闭区域的面积S.
轴围成的封闭区域的面积S.
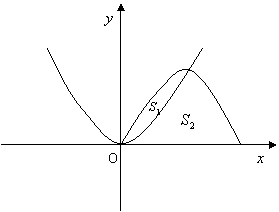
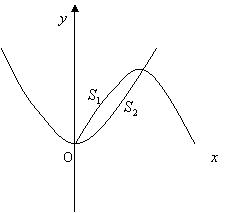
(2)如图,若抛物线![]() 将(1)中的区域分成两部分,面积分别为
将(1)中的区域分成两部分,面积分别为![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
 |
17.(满分12分)
 | |||
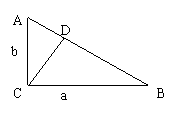 | |||
已知在△ABC中![]() 且
且![]() ,
,
![]() ,则
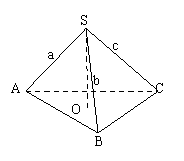
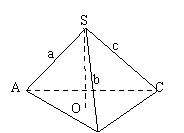
,则![]() ;拓展到空间,如右图,三棱锥
;拓展到空间,如右图,三棱锥![]() 的三条侧棱SA、SB、SC两两垂直,
的三条侧棱SA、SB、SC两两垂直,![]() ABC上的射影为O.运用类比猜想,对于上述的三棱锥
ABC上的射影为O.运用类比猜想,对于上述的三棱锥![]() 存在什么类似的结论,并加以证明.
存在什么类似的结论,并加以证明.
18.(满分14分)对于任意正整数![]() ,比较
,比较![]() 与
与![]() 的大小,并用数学归纳法证明你的结论.
的大小,并用数学归纳法证明你的结论.
19. (满分14分)已知抛物线![]() 焦点为F,分别与抛物线切于点A、B的两切线
焦点为F,分别与抛物线切于点A、B的两切线![]() 、
、![]() 互相垂直,
互相垂直,
(1)求证:A、F、B三点共线;
(2)过A、B两点的直线为![]() ,点M在
,点M在![]() 上,若
上,若![]() (O为坐标原点),求点
(O为坐标原点),求点![]() 的轨迹方程.
的轨迹方程.
20.(满分14分) 设不等式组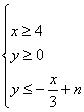 所表示的平面区域为
所表示的平面区域为![]() ,记
,记![]() 内的整点个数为
内的整点个数为![]()
![]() ,(整点即横坐标和纵坐标均为整数的点).
,(整点即横坐标和纵坐标均为整数的点).
(1)求![]() 、
、![]() ;
;
(2)猜想![]() 的通项公式(不需证明);
的通项公式(不需证明);
(3)记![]() ;
;![]() ,
,
若![]() 求
求![]() 的值.
的值.
 |
高二年级数学科答题卷
考试时间:120分钟 满分:150分 命题教师:ZXL
| 题号 | 一 | 二 | 三 | 总分 | |||||
| 15 | 16 | 17 | 18 | 19 | 20 | ||||
| 得分 |
|
|
|
|
|
|
|
|
|
一. 选择题(每题5分,共40分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答案 |
二.填空题(每题5分,共30分)
9.______________________; 10._______________________;
11._______________________; 12.________________________.
13.________________; 14._________ __________ _____________.
三.解答题(本题共6小题,80分,解答应写出文字说明,证明过程或演算过程.)
15.(12分)
|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
|
|
|
|
18.(14分)
19. (14分)
20. (14分)
湛江一中2007—2008学年度第二学期期中考试
高二年级数学(理)科参考答案
一. 选择题(每题5分,共40分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答案 | C | D | B | D | B | A | A | A |
二.填空题(每题5分,共30分)
9.
1;
10. ![]() ;
;
11. 36; 12. 7.
13.![]() ;
14.
;
14. ![]()
![]()
![]()
三.解答题(本题共6小题,80分,解答应写出文字说明,证明过程或演算过程.)
15.(12分)
![]()
![]() ………………………6分
………………………6分
![]()
![]()
于是不存在常数项. ………………………6分
 16.(满分14分)
16.(满分14分)
(1)令![]() ,得
,得![]()
![]() ………………………6分
………………………6分
![]() (2) 由
(2) 由![]() ,得
,得![]()
![]()
![]()
![]() ………………………14分
………………………14分
|
 17.(满分12分)
17.(满分12分)
猜想:![]() ………………………4分
………………………4分
后面的证明8分
18.(14分)
![]()
![]()
![]() ………………………4分
………………………4分
后面的证10分
19. (14分)
解:(1)![]()
![]()
![]() ………………………3分
………………………3分
![]()
![]()
![]() ………………………7分
………………………7分
(2)由(1)所证得直线![]() 过点
过点![]() ,又因为
,又因为![]() 且M在
且M在![]() 上
上
![]() 点轨迹是以
点轨迹是以![]() 为直径的圆
为直径的圆
![]() 点的轨迹方程为
点的轨迹方程为![]() ………………………14分
………………………14分
20. (14分)
![]() ……4分
……4分
(2)![]() ………………………7分
………………………7分
(3) n=2008 ………………………14分