高二数学直线与平面检测题
姓名 班级编号 分数
一、选择题（每小题5分，共50分）
1．空间四边形
中，
、
两异面直线成
角且
，
、
、
、
分别是
、
、
、
的中点，则四边形
的面积是（ ）
A．1
B．
2．下列命题中，正确的是（ ）
①
与
有无数个公共点
②
与有一个公共点
③与无公共点
④
与的关系可分为
或
A．①② B．①③ C．①④ D．②③
3．在空间四边形中，
，
，、分别是、的中点，则
与所成角的大小为（ ）
A．
B．
C．
D．以上都不对
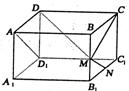4．在长方体
中，
、
分别是棱
，
的中点，若
，则异面直线
与
所成的角为（ ）
A． B． C．
D．
5．给出下列命题：
①直线上有两点到平面的距离相等，则此直线与平面平行
②夹在两个平行平面间的两条异面线段的中点连线平行于这两个平面
③直线
，直线
，则
④、
是异面直线，则存在唯一平面，使它与、都平行且与、距离相等
其中正确的命题是
A．①② B.②③ C.③④ D.②④
6．
在平面内，
，
是的斜线，
，则点
在上的射影在（ ）
A．直线上 B．直线上 C．直线上 D．内部
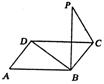
7．如右图，正方形，
，
平面，则
与所成的角是（ ）
A．
B． C． D．
8．设、是平面外的任意两条线段，则“、的长相等”是“、在平面内的射影长相等”的（ ）
A．既不充分也不必要条件 B．充分必要条件
C．必要不充分条件 D．充分不必要条件
9．两条相交直线
都在平面内且都不在平面
内。命题甲：
和
中至少有一条与 相交，命题乙：平面与相交，则甲是乙的（ ）
A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要
10．如右图所示，正方体中，、、、、、分别是所在
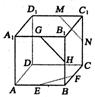棱的中点，则下列结论正确的是（ ）
A．直线
和
平行，和相交
B．直线和平行，和相交
C．直线和相交，和异面
D．直线和异面，和异面
答 题 卡
| 题 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答 案 |
|
|
|
|
|
|
|
|
|
|
二、填空题（每小题5分，共25分）
11．关于直角
在平面内的射影有如下判断：①可能是
的角；②可能是锐角；③可能是直角；④可能是钝角；⑤可能是
的角。其中正确判断的序号是
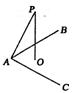12．如图所示,
,点在平面
外,
,
,
平面于
,并且
,则线段的
长为
13．菱形,已知
,垂直于所
在的平面且
,则到
的距离是
;到的距离 为
.
14．直角三角形所在平面外一点到直角顶点
的距离为
,到两直角边的距离都是
,则到平面的距离是
15．已知直线
及平面
，给出下列命题：
①若
则
；②若
则
；③若
则
；④若
则
或
异面。
其中正确命题的序号是
三、解答题
16. 长方体的底面是边长为
的正方形,
,在棱
上,且
,求证:
平面
.
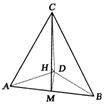
17．已知等腰
中,
以边上的高为折痕,把对折,对折后
,求对折后
与在平面上的射影之间的距离.
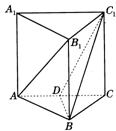18．如图所示,正三棱柱
的底面边长为
,对角线
,为的中点.(1)求证:
平面
(2)求异面直线
与
所成角的度数.
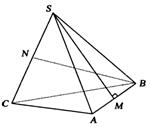19．
是正三角形所在平面外一点,如图,
,且
,分别是和
的中点.求异面直线
与
所成的角.
20．在长方体中,已知、各为
和
的中点.(1)求证:平行于侧面
;(2)求证:
;(3)若
求证:垂直于面
.
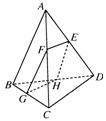21．如图,在四面体中,截面
平行于对棱和,试问点在什么位置时其截面面积最大.
参考答案：
一、选择题 BCCDD CCACB
二、填空题 11.①②③④⑤ 12.
13.10;10
14.12 15.①③
三、解答题
16.证明:连结
是正方形,
又
平面
平面 
而
故平面
17.解：取中点，连结
，作
于
由已知得
而
平面
又
平面
是在平面上的射影
在等腰
中，
又由已知
即对折后与在平面上的射影之间的距离是
18.（1）证明：连结
交于，连
，则
，又
平面
，
平面
平面
（2）解：
（或其补角）就是与所成的角
在
中，
，
故异面直线与所成的角为
19.解：连结
，取的中点，连
（或其补角）就是异面直线与所成的角。
设
则
在
中，
在
中，
；
在
中，
异面直线与所成角为
20.证明：（1）延长交于点，易知为中点，连接
由
知
是平行四边形 
而
平面，
平面 
平面
（2）
平面，平面 
而
（3）
是正方形
又
由（2）知且
平面
21.解：由已知可证四边形是平行四边形
所成角为异面直线
所成的角，
故
为定值。
设
当且仅当
即为中点时，取等号。
故点在中点时，截面面积最大。