高中数学必修4期中考试卷
(时间：120分钟)
重要说明：本试卷将评出两个成绩，第Ⅰ卷成绩为模块考试成绩，第Ⅰ、Ⅱ卷总成绩折算成百分制后为期中综合成绩，没有附加题。
第Ⅰ卷（100分）
一、选择题：（每小题3分，共36分）
1、
的值是（ ）
A．
B．－ C．
D．－
2、化简
－
得（ ）
A．
B．－ C．
D．－
3、如果角
的终边经过点（－，），那么
的值是（ ）
A． B．－ C．
D． － 
4、函数f(x)=
的周期、振幅、初相分别是（ ）
A．
，2，
B．4，－2，－
C．4，2， D．2，2，
5、对于非零向量a、b，下列命题中错误的是（ ）
A．a·b＝b·a B．a2＝
C．a
b
a·b＝(a·b)2 D．a∥ba在b上的投影为
6、已知a＝(5，－2)，b＝(－4，－3), c＝(x，y)，若a－2b＋
A．(1，
) B．(
，) C．(
，
) D．(－，－)
7、在平行四边形ABCD中，
，
，
，
，则下列运算正确的是（ ）
A．a＋b＋c＋d＝0 B．a－b＋c－d＝0
C．a＋b－c－d＝0 D．a－b－c＋d＝0
8、函数y＝1－2
的最小值、最大值分别是（ ）
A．－1，3 B．－1，
9、已知
，
，那么角2
的终边所在的象限是（ ）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
10、已知
，
，那么
的值是（ ）
A．－
B．－
C．－
D．
11、若
，
，则实数
的值是（ ）
A．
B． C． D．－
12、已知
的三个顶点A、B、C及平面内一点P，若
，则点P与的位置关系是（ ）
A．P在AC边上 B．P在AB边上或其延长线上
C．P在外部 D．P在内部
二、填空题：（每小题4分，共16分）
13、在学习平面向量的线性运算中，多处使用了类比的方法，是类比了 .
14、观察以下三个等式：
，
试写出一个与以上各式具有共同特点的等式： .
15、函数
的图象可以先由
的图象向 平移 个单位，然后把所得图象上各点的横坐标 为原来的 倍(纵坐标不变)而得到.
16、已知向量
＝(k，12)，
＝(4，5)，
(－k，10)，且A、B、C三点共线，则k＝
.
三、解答题：（共48分）
17、(10分)已知锐角、
满足
，
，求＋的值.
18、(12分)已知函数
.
⑴求函数的递减区间；
⑵求函数的最小值及此时x的集合.
19、(12分)若
、
是夹角为60°的两个单位向量，
，
，
⑴求
·
的值；
⑵求、的夹角.
20、(14分)试从“和角余弦公式”：
出发，利用诱导公式和同角基本关系式推导出其余5个和角、差角公式.
第Ⅱ卷（40分）
友情提示：注意掌握时间，会做的要先做，不要放弃任何得分的机会。
21、(6分)已知向量＝(6，－8)，求与平行的单位向量
.
22、(10分)在矩形ABCD中，AB＝a，BC＝2a.
在BC上取一点P，使AB＋BP＝PD，求
的正切值.
23、(10分)已知：积
的结果可写成
的形式.
⑴试通过三个实例(取具体角)，分别计算积的值；
⑵猜想积的一般结果，并给出一般性证明.
24、(14分)已知
，
，且
，求：
⑴·及
；
⑵若
的最小值为－
，求实数的值.
莆田一中2006～2007学年下学期期中考答题卷
高一数学(必修4)
一、选择题：（每小题3分，共36分。请填入答题卡中。）
二、填空题：（每小题4分，共16分）
13、 ；15、 ；
15、 、 ， 、 ；16、 .
三、解答题：
17、(10分)
18、(12分)
19、(12分)
20、(14分)
21、(6分)
22、(10分)
23、(10分)
24、(14分)
莆田一中2006～2007学年下学期期中考参考答案
高一数学（必修4）
一、选择题：（每小题3分，共36分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | A | D | C | D | D | B | A | D | B | D | A |
二、填空题：（每小题4分，共16分）
13、实数运算的相关性质（等） 14、
(等)
15、左、
；缩短、
16、－
三、解答题：（共48分+40分）
17、(10分)解：∵、为锐角，且，
∴
，
(4分)
∴
(8分)
∵
，∴
（注：解为
的扣2分。） (10分)
18、(12分)解：
(4分)
⑴由
，得
∴所求递减区间是[
]（
） (8分)
⑵当
＝－1时，
这时
，所求集合是
(12分)
（注：没写区间扣1分，区间后没 ()扣1分，没用集合表示扣1分。）
19、(12分)解：⑴
(2分)
∵
(4分)
∴
＝－3.5 (6分)
⑵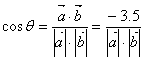
(8分)
∵
,
(10分)
∴
，∵
，∴
答（略） (12分)
20、(14分)略。注：少证一个或证错一个扣3分。
21、(6分)解：∥，∴
(2分)
由
，得
(4分)
∴
。（注：少一解扣2分） (6分)
22、(10分)解：设BP＝x，则PC＝2a－x，设
，
则
，
，
(2分)
(6分)
∵AB＋BP＝PD，∴a＋x=
化简得
(8分)
∴
(10分)
23、(10分)解：⑴当
时，原式＝
不存在，
当
时原式＝
当
时原式＝
当
时原式＝
(3分)
⑵猜想：
(5分)
证明：左边＝
右边＝
左边
∴猜想成立。 (10分)
24、(14分)解：⑴
(2分)
∵
∴
＝
（∵
） (6分)
⑵f(x)＝
=
(8分)
∵，∴
，1]
①当
[0，1]时，取
，
得
，∴
(10分)
②当<0时，取
0，得
（不合）
③当>1时，取1，得
，
（不合）
∴综上所述，实数的值为 (14分)
（注：没分类讨论扣4分。）