高二下3月月考数学(理)试卷
第一卷
一 选择题 (每小题4分共40分)
1, 如果复数
的实部和虚部互为相反数，那么实数b的值为
－2i
－
2,
3,下面的四个不等式: ①
②
③
④
, 其中不成立的有
1个
2个
3个
4个
4, 甲、乙、丙三家公司承包6项工程, 甲承包3项,乙承包2项,丙承包1项,不同的承包方案有
( )种
5, 已知随机变量X的分布列如下表（其中a为常数）：
| X | 0 | 1 | 2 | 3 | 4 |
| P | 0.1 | 0.2 | 0.4 | 0.2 | a |
则下列计算结果错误的是
6, 在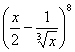
的展开式中,常数项是
7, 有一段演绎推理是这样的：“直线平行于平面,则平行于平面内所有直线；已知直线
∥平面
，直线
平面，则直线∥直线
”的结论显然是错误的，这是因为
推理形式错误 大前提错误 小前提错误 非以上错误
8,
除以8的余数是
7
1
3
2
9, 甲、乙两人练习射击, 命中目标的概率分别为
和
, 甲、乙两人各射击一次,有下列说法:
① 目标恰好被命中一次的概率为
② 目标恰好被命中两次的概率为
③ 目标被命中的概率为
④目标被命中的概率为 
以上说法正确的序号依次是
②③
①②③
②④
①③
10, 平面内有
条直线,其中任何两条不平行,任何三条不共点,则这条直线把平面分割成( )个区域
二, 填空题 (每小题4分共16分)
11, 若复数
同时满足
为虚单位), 则
12, 对于下式,
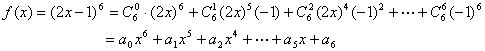
有如下结论:
① 
②
③ 
正确的结论为:
(只填正确选项的序号)
13, 已知某种子的发芽率为, 现随机种下这样的种子3粒,则恰好有2粒发芽的概率为
14,一个类似于杨辉三角的三角形数组（如下图）满足：
（1）第1行只有1个数1；
（2）当n≥2时，第n行首尾两数均为n;
(3)当n>2时，中间各数都等于它肩上两数之和，
则第n行（n≥2）的第2个数是___________
1
2 2
3 4 3
4 7 7 4
…………………………………………………………
高二下3月月考数学(理)试卷
第二卷
二、填空题答案 (每小题4分共16分)
11、 ； 12、 ；
13、 ； 14、 ；
三、解答题（共44分）
15,
(满分8分) 已知抛物线
(1) 若直线
与抛物线相切于点
,试求直线的方程? (4分)
(2)若直线过点
,且与
轴平行,求直线与抛物线所围成的封闭区域的面
积? (4分)
16, (满分9分)
(1) 6个人站成一排, 其中甲、乙、两三必须相邻的排法有多少种? (3分) (作具体数字作答)
(2) 从1、3、5、7中任选两个数, 从0、2、4、6中任选两个数, (3分)
一共可以组成多少个四位数? (用具体数字作答)
(3) 若
,求出
的值 (算出具体数字) (3分)
17, 已知6件产品中, 有2件次品,现从中任取3件,试求 (9分)
(1) 所取出的3件产品中最多有1件次品的概率? (概率用分数表示) (3分)
(2) 取出的3件产品中所含次品数
的分布列? (概率用分数表示) (6分)
18, (满分9分)
某轮船航行过程中每小时的燃料费
与其速度
的立方成正比,已知当速度为10千米/小时,燃料费10元/小时,其他与速度无关的费用每小时160元,设每千米航程成本为
,
(1) 试用速度表示轮船每千米航程成本 (3分)
(2) 轮船的速度为多少时,每千米航程成本最低? (6分)
19, （满分9分）
(1) 已知
的三条边分别为
, 用分析法证明:
(3分)
(不用分析法证明给分)
(2) 已知数列
的通项公式
,记 (6分)
,
①求
并猜出
的表达式. (2分)
②用数学归纳法证明你的猜想. (4分)
 |
参考答案
一, 选择题
1,B 2, A 3,B 4,B 5,D 6,C 7, C 8, C 9,A 10,C
二,填空题
11, 
12,
0.20736 13, 
14, 一
三,解答题
15,(1) 
或
(2) 
且 
(3) 
16,(1) 1631 (2) 156 (3) 115
17,(1)的分布列为
|
| 1 | 2 | 3 | 4 |
|
|
|
|
|
|
(2)
18,(1) 
(2) 
耗油
19,(1) 
,猜想: 
(2) 证明: 略