高二年理科数学下学期期中考试卷 2008、4、17
(考试时间:120分钟 总分:150分)
一、选择题(每小题5分,共60分)
1、设![]() 是可导函数,且
是可导函数,且![]() (▲▲▲)
(▲▲▲)
A.![]() B.
B.
2、一个口袋内装有大小相同的6个白球和2个黑球,从中取3个球,则共有(▲▲▲)种不同的取法.
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
3、设![]() ,则(▲▲▲)
,则(▲▲▲)
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
4、曲线![]() 在
在![]() 处的切线的倾斜角是(▲▲▲)
处的切线的倾斜角是(▲▲▲)
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
5、![]() 则
则![]() 等于(▲▲▲)
等于(▲▲▲)
A、0 B、![]() C、
C、![]() D、
D、![]()
6、函数![]() ,
,![]() 的最大值、最小值分别是(▲▲▲)
的最大值、最小值分别是(▲▲▲)
A、3,-17 B、1,-1 C、1,-17 D、9,-19
7、平面内平行于同一直线的两直线平行,由类比思维,我们可以得到(▲▲▲)
A、空间中平行于同一直线的两直线平行 B、空间中平行于同一平面的两直线平行
C、空间中平行于同一直线的两平面平行 D、空间中平行于同一平面的两平面平行
8、某城市新修建的一条道路上有12盏路灯,为了节省用电而又不能影响正常的照明,可以熄灭其中的3盏灯,但两端的灯不能熄灭,也不能熄灭相邻的两盏灯,则熄灯的方法有(▲▲▲)
A.![]() 种 B.
种 B.![]() 种 C.
种 C.![]() 种 D.
种 D.![]() 种
种
9、![]() 等于(▲▲▲)
等于(▲▲▲)
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
10、如果函数![]() 有单调递减区间,则(▲▲▲)
有单调递减区间,则(▲▲▲)
A.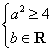 B.
B.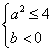 C.
C.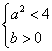 D.
D.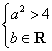
11、已知![]() (a为常数)在[-2,2]上有最大值3,那么在[-2,2]上f(x)的最
(a为常数)在[-2,2]上有最大值3,那么在[-2,2]上f(x)的最
小值是(▲▲▲)
A. -29 B.-
12、一个作直线运动的物体,它的速度![]() (米/秒)与时间t(秒)满足
(米/秒)与时间t(秒)满足![]() ,如果它在a秒内的平均速度与2秒时的瞬时速度相等,则a等于(▲▲▲)
,如果它在a秒内的平均速度与2秒时的瞬时速度相等,则a等于(▲▲▲)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(每小题4分,共16分)
13、已知![]() ,
,![]() ,试通过计算
,试通过计算![]() ,
,![]() ,
,![]() ,
,![]() 的值,推测出
的值,推测出![]() =
.
=
.
14、垂直于直线![]() 且与曲线
且与曲线![]() 相切的直线方程的一般式是
相切的直线方程的一般式是
15、抛物线![]() 与过它的顶点倾斜角为
与过它的顶点倾斜角为![]() 的直线l所围成的图形的面积是 .
的直线l所围成的图形的面积是 .
16、8个身高不相同的人排成前后两排,每排4人,要求后排的人都比他对应的前排的人高,则不同的派法有 种.(用数字作答)
高二年数学期中考试答题卷
| 选择题 | 填空题 | 17 | 18 | 19 | 20 | 21 | 22 | 总分 |
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题:
13、 14、 15、 16、
三、解答题
17、计算求值(本题满分12分,每小题6分)
(1)计算![]() (2)已知复数
(2)已知复数![]() 满足
满足![]() 求
求![]()
18、(本题满分12分) 已知曲线![]()
(1)求曲线在点![]() 处的切线方程 (2)求曲线过点
处的切线方程 (2)求曲线过点![]() 的切线方程
的切线方程
19、(本题满分12分)从8名运动员中选4人参加4×
(1)甲、乙两人必须跑中间两棒; (2)若甲、乙两人只有一人被选且不能跑中间两棒;
(3)若甲、乙两人都被选且必须相邻两棒.
20、(本题满分12分)已知数列![]() 前
前![]() 项和为
项和为![]() 且
且![]() ,
,![]()
(1)试求出![]() ,
,![]() ,
,![]() ,
,![]() ,并猜想
,并猜想![]() 的表达式 (2)证明你的猜想,并求
的表达式 (2)证明你的猜想,并求![]() 的表达式
的表达式
21、(本题满分12分) 已知函数![]() =
=![]() 在x=1处取得极值2.
在x=1处取得极值2.
(1)求函数![]() 的解析式; (2)实数m满足什么条件时,函数
的解析式; (2)实数m满足什么条件时,函数![]() 在区间
在区间![]() 上单调递增?
上单调递增?
22、(本题满分14分)已知函数![]() 在
在![]() 处取得极值
处取得极值
(1)求实数![]() 的值;
的值;
(2)若![]() 时
时![]()
![]() 恒成立,求实数b的取值范围;
恒成立,求实数b的取值范围;
(3)证明对任意的正整数![]() ;不等式
;不等式![]() 都成立
都成立
高二年数学期中考试参考答案
一、选择题(每小题5分,共60分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | D | D | C | A | A | D | A | B | D | B | C |
二、填空题(每小题4分,共16分)
13、![]() 14、
14、![]() 15、
15、![]() 16、2520
16、2520
17、解(1)![]()
![]()
![]()
![]()
![]()
(2)设![]() 则
则![]()
![]()
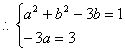
![]() 或
或![]()
![]() 或
或![]()
18、解:(1)![]()
![]()
![]() 所求切线方程为
所求切线方程为![]() 即
即![]()
(2)设切点![]()
则切线方程为![]() 又切线过点
又切线过点![]()
![]()
![]() 或
或![]()
![]() 切线方程为
切线方程为![]() 或
或![]()
19、解:(1)![]()
(2)![]()
(3)![]()
20、解:(1)![]()
![]()
![]()
![]()
猜想![]()
(2)证明①当![]() 时
时 ![]() 成立
成立
②假设![]()
![]() 时,
时,![]() 成立
成立
那么![]() 时
时
![]()
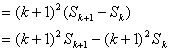
![]()
![]() 时命题成立
时命题成立
由①②可知,对于一切![]()
![]() 均成立
均成立
由![]()
21、解:(1)已知函数![]() =
=![]() ,
,![]() .
……………………2分
.
……………………2分
又函数![]() 在x=1处取得极值2,
在x=1处取得极值2,![]() 即
即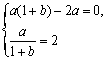
![]()
![]() . …………………5分
. …………………5分
(2)由![]() . …………………7分
. …………………7分
| x |
|
| (-1,1) | 1 |
|
|
| - | 0 | + | 0 | - |
|
| 单调递减 | 极小值-2 | 单调递增 | 极大值2 | 单调递减 |
所以![]() 的单调增区间为
的单调增区间为![]() .
………………………9分
.
………………………9分
若![]() 为函数
为函数![]() 的单调增区间,则有
的单调增区间,则有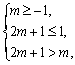 解得
解得![]()
即![]() 时,
时,![]() 为函数
为函数![]() 的单调增区间. ………………………12分
的单调增区间. ………………………12分
22、解:(Ⅰ)![]()
![]() 时,
时,![]() 取得极值,
取得极值,![]() ,
,
故![]() 解得
解得![]() 经检验
经检验![]() 符合题意。
符合题意。
(Ⅱ)由![]() 知
知![]() 由
由![]()
得![]() ,
,
令![]() ,
,
![]() ,
,
当![]() 时,
时,![]() ,于是
,于是![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() ,于是
,于是![]() 在
在![]() 上单调递减。
上单调递减。
![]()
![]()
