高二年级数学上学期期末考试试卷(文科)
命题人 鞍山一中 李燕溪 校对人 李燕溪
一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一个选项是符合题目要求的．
1．椭圆
的离心率是
（ ）
A.
B. 
C.
D.
2．
则
是该数列中的
（ ）
A 第9项 B 第10 项 C 第11项 D 第12项
3．在
中, 
则AC边长为
( )
A.
B. 
C. 
D. 
4. 过抛物线y=x2上的点M（
，
）的切线的倾斜角是
（ ）
A 
B 
C 
D 
5.设
在
上的图象是一条连续不间断的曲线，且在
内可导，
则下列结论中正确的是 （ ）
A. 的极值点一定是最值点 B. 的最值点一定是极值点
C. 在此区间上可能没有极值点 D. 在此区间上可能没有最值点
6.集合
,
,若
则实数P的取值范围是（ ）
A. 
B. 
C. 
D. 
7.已知数列
,如果
(
)是首项为1公比为
的等比数列，那么
等于 （ ）
A. 
B. 
C. 
D. 
8.已知椭圆
和双曲线
有公共的焦点，那么双曲线的渐近线方程为
（ ）
A. 
B. 
C. 
D. 
9.已知函数
的图象如图所示
（
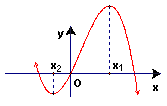为两个极值点），且
则有
（ ）
A. 
B. 
C. 
D. 
10.已知直线y=kx-k及抛物线
，则
（ ）
A.直线与抛物线有且只有一个公共点
B.直线与抛物线有两个公共点
C.直线与抛物线有一个或两个公共点
D.直线与抛物线可能没有公共点
11在椭圆
上有一点P，F1、F2是椭圆的左、右焦点，△F1PF2为直角三角形，则这样的点P有
（ ）
A 4个 B 6个 C 8个 D 2个
12．已知梯形的两底的长度分别为
。将梯形的两腰各分为n等份，连结两腰对应的分点，得到n-1条线段的长度之和为
（ ）
A. 
B. 
C. 
D. 
二、填空题：本大题共4小题，每小题4分，共16分．
13.数列｛｝为等差数列，
14.已知x,y满足条件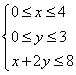
则z=2x+5y的最大值为
15.函数
的最小值是
.
16. 给出下列三个命题
(1)设是定义在R上的可导函数.
是
为极值点的
必要不充分条件
(2)双曲线
的焦距与m有关
（3）命题“中国人不都是北京人”的否定是“中国人都是北京人”。
其中正确命题的序号是 。
三、解答题：本大题共6小题，共74分，解答应写出文字说明、证明过程或演算步骤．
17．（本小题满分12分）已知在△ABC中，角A、B、C所对的边分别为a,b,c, a=7， b=3， c=5，
（1）求△ABC中的最大角；
（2）求角C的正弦值。
18．（本小题满分12分）要建一间地面面积为
19．（本小题满分12分）定义在R上的函数ƒ(
)=
+
+
(,为常数)，在=－1处取得极值，ƒ()的图象在P（1，
ƒ(1)）处的切线平行直线
＝8，
（1）
求函数ƒ()解析式；
（2）
求函数ƒ()极值。
20．（本小题满分12分）数列｛｝的前n项和记为
，1＝1，
（n≥1）.
（1）
求｛｝的通项公式；
（2）
等差数列｛
｝的各项为正数，其前n项和为
，且
＝15，又1+1，
+
，
+
成等比数列，求
21．（本小题满分12分）已知曲线C上任意一点M到点F（0，1）的距离比它到直线
＝
的距离小1.
（1）求曲线C的方程；
（2）若过点P（2，2）的直线m与曲线C交于A，B两点，设
.
（i）当λ＝1时，求直线m的方程；
（ii）当△AOB的面积为时（O为坐标原点），求λ的值.
22．（本小题满分14分）
已知函数
在
是增函数，
在（0，1）为减函数。
（1）求
的表达式；
（2）当b＞
时，若对于任意的x∈（0，1 ]，都有
≥
在
∈（0，1 ]上恒成立，求b的取值范围.
2007—2008学年度上学期期末考试高二年级数学科试卷
文科答案
一、
二 13、21-2n 14、19 15、5 16、（1）（3）
17. 
............6分
............12分
18、解 设地面的长为x，则宽为
，总造价为y，y=
............6分
36500
............10分
当且仅当x=时取等，即长、宽相等都为
............12分
解：
19、（1）由题设知
ƒ()＝3+22+，
............6分
(2)
，
令
，
............8分
当变化时，ƒ()
的变化情况如下表：
|
| （－ | －1 | （－1， |
| （ |
|
| + | 0 | － | 0 | + |
| ƒ( | ↑ | 0 | ↓ |
| ↑ |
，－1）
ƒ()的极大值为ƒ（-1）＝0，极小值为ƒ（
）＝
........12分
20、
（1）
由（n≥1）可得
（n≥2）,两式相减得n+1－n=2
n，
.
又2＝2S1+1=3,
，故｛n｝是首项为1，公比为3的等比数列，
.
............6分
（2）设｛n｝的公差为
，由T3＝15可得1+2+3＝15，可得2＝5，故可设1＝5－，3＝5+.
又1＝1，2＝3，3＝9，由题意可得（5－+1）（5++9）＝（5+3）2，解得1＝2，2＝－10.
等差数列｛n｝的各项为正，＝2，
.
............12分
21、解: （1）解法一
设
当≥-2时；
；
当＜-2时，
两边平方得
，因＜-2，不合题意，舍去.
故点M的轨迹C的方程是：
.
............4分
解法二 ∵点M到点F（0，1）的距离比它到直线＝-2的距离小1.
∴点M在直线
的上方. ∴点M到F（0，1）的距离与它到直线
＝-1的距离相等.
∴点M的轨迹C是以F为焦点
为准线的抛物线，所以曲线C的方程为.
（2）当直线m的斜率不存在时，它与曲线C只有一个交点，不合题意，
当直线m与轴不垂直时，设直线m的方程为
.
代入得，
①
＞0对k∈R恒成立.
∴直线m与曲线C恒有两个不同的交点。
设交点A，B的坐标分别为A（
）B（
），则
. 
.
（i）由，且λ＝1得，P为AB的中点，
∴
.把②代入得，
.∴直线m的方程是
.
............6分
（ii）
＝
.
点O到直线m的距离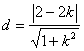
.
=
·
=
∵=
∴
.
（
（无实根）
由
1°当k＝0时，方程①的解为
.
当
＝
；
当
. ...........10分
2°当k＝2时，方程①的解为
，
同理可得，
.
............12分
22、（1）∵
，依题意
＞
∈（1，2]）, ∴＜
，
∴≤2.
............2分
又∵
，依题意
＜0（∈（0，1）），∴＞
，
∴
≥2.
............4分
∴=2，∴
。 ............6分
（2）∵
，
∴当∈（0，1］时为减函数，其最小值为1. ............8分
令
.
∵b＞-1，t∈（0，1］，∴
＞0在（0，1］恒成立.
∴函数
在t∈（0，1］为增函数，其最大值为2b-1，依题意
，解得-1＜b≤1为所求范围.
............14分