高二文科数学第二学期期中考试
2008.04.29
本试卷分选择题和非选择题两部分,共7页。满分为150分,考试时间120分钟。
参考公式: ![]()
第一卷
一、选择题:本大题共10个小题,每小题5分,共50分。每小题给出的四个选项中,有且只有一项是符合题目要求的,请把选出的答案代号填在第二卷的选择题答题表内。
1.抛物线![]() 的准线方程是( ).
的准线方程是( ).
A. ![]() B.
B.
![]() C.
C. ![]() D.
D.
![]()
2. 在复平面内,复数![]() 对应的点位于(
).
对应的点位于(
).
A.第一象限 B.第二象限 C.第三象限 D.第四象限
![]() 为纯虚数的( )
为纯虚数的( )
(A)充分条件 (B)必要条件
(C)充要条件 (D)非充分非必要条件
4.曲线![]() 在点
在点![]() 处的切线方程是( ).
处的切线方程是( ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
5.按照下列三种化合物的结构式及分子式的规律,
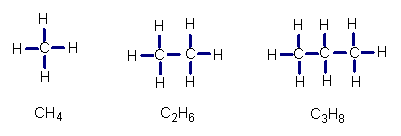
写出后一种化合物的分子式是( ).
A.C4H9 B.C4H
6、用反证法证明命题“如果![]() ”时,假设的内容应是( )
”时,假设的内容应是( )
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
7、凡自然数都是整数,而 4是自然数 所以,4是整数。以上三段论推理( )
(A) 正确 (B) 推理形式不正确
(C)两个“自然数”概念不一致 (D) 两个“整数”概念不一致
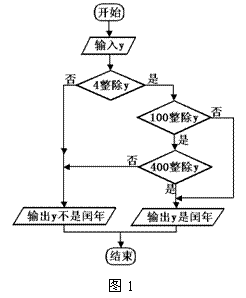 |
8.如图1所示,是关于闰年的流程,则以下年份是
闰年的为 ( )
A.1996年
B.1998年
C.2010年
D.2100年
9.设![]() ,
,![]() ,
,![]() ,……,
,……,![]() (n∈N),则f2008(x) =( ).
(n∈N),则f2008(x) =( ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
10.若![]() 且
且![]() ,则
,则![]() 的最小值是:( )
的最小值是:( )
A 2 B
二, 填空题 (每小题5分共25分,请把答案填在第二卷)
11. 在极坐标系中,点![]() 到直线
到直线![]() 的距离为
.
的距离为
.
12、经过点![]() 且与双曲线
且与双曲线![]() 有共同渐近线的双曲线方程为
有共同渐近线的双曲线方程为
。
13.已知x与y之间的一组数据:
| x | 0 | 1 | 2 | 3 |
| y | 1 | 3 | 5 | 7 |
则y与x的线性回归方程为y=bx+a必过点 .
14.直线![]() 被圆
被圆![]() 所截得的弦长为
.
所截得的弦长为
.
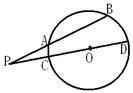 15.如图,已知⊙O的割线PAB交⊙O于A,B两点,割线PCD经过圆心,若
15.如图,已知⊙O的割线PAB交⊙O于A,B两点,割线PCD经过圆心,若![]() ,
,![]() ,
,![]() ,则⊙O的半径为_______________.
,则⊙O的半径为_______________.
三、解答题(共75分)请把答案填在第二卷
16.(1)(6分)我校学生会有如下部门:文娱部、体育部、宣传部、生活部、学习部。
请画出学生会的组织结构图。
(2)(8分)给出如下列联表
|
| 患心脏病 | 患其它病 | 合 计 |
| 高血压 | 20 | 10 | 30 |
| 不高血压 | 30 | 50 | 80 |
| 合 计 | 50 | 60 | 110 |
由以上数据判断高血压与患心脏病之间在多大程度上有关系?
(参考数据:![]() ,
,![]() )
)
17、(本小题满分10分)计算:![]() +
+![]()
18.(本小题满分12分)已知![]() ,并且
,并且![]() ,用分析法证明:
,用分析法证明:![]()
19.已知数列![]() 的通项公式
的通项公式![]() ,记
,记![]() ,试通过计算
,试通过计算![]() 的值,推测出
的值,推测出![]() 的值. (12分)
的值. (12分)
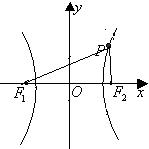 20.设动点
20.设动点![]() 到点
到点![]() 和
和![]() 的距离分别为
的距离分别为![]() 和
和![]() ,
,![]() ,且
,且![]() .
.
(1)求证:![]() ;
;
(2)求动点P的轨迹方程. (13分)
21. (本小题满分14分)已知直线![]() 与椭圆
与椭圆![]() 相交于A、B两点.
相交于A、B两点.
(1)若椭圆的离心率为![]() ,焦距为2,求线段AB的长;
,焦距为2,求线段AB的长;
(2)在(1)的椭圆中,设椭圆的左焦点为F1,求△ABF1的面积。
台山侨中2007-2008学年度第二学期期中考试
高二文科数学 2008.04.29
第二卷
| 题号 | 一 | 二 | 16 | 17 | 18 | 19 | 20 | 21 | 总分 |
| 得分 |
一、选择题:(本大题共10小题,每小题5分,共5 0分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二、填空题:(本大题共5小题,每小题5分,共25分)
11. 12.
13. 14.
15.
三、解答题(本大题共6小题,共75分,解答时应写出文字说明、证明过程或演算步骤。)

 16(1)【解】
16(1)【解】
(2)【解】
17 【解】
18 【解】
19 【解】

20 【解】
21 【解】
台山侨中2007-2008学年度第二学期期中考试
高二文科数学参考答案及评分标准 2008.04.29
一、选择题 每小题5分 BDBDB CACAA
二、填空题 每小题5分
11. ![]() .
12、
.
12、 ![]()
13.(1.5,4) 14.![]() 15.R=2
15.R=2
16(6分)解:学生会的组织结构图如下:
 |
(全部正确6分,否则0分)
(8分)解:由列联表中的数据可得
![]() 4分
4分
又![]() 6分
6分
所以有90%的把握认为高血压与患心脏病有关。 8分
17、(本小题满分10分)计算:![]() +
+![]()
解:原式=![]() ……4分
……4分
=![]() ……6分
……6分
=![]()
![]() ……8分
……8分
= i-i
= 0 ……10分
18已知![]() ,并且
,并且![]() ,用分析法证明:
,用分析法证明:![]()
证明: ∵![]() ,∴
,∴![]()
要证![]()
只需证![]() ……5分
……5分
只需证![]()
只需证![]()
又![]() ∴只需证
∴只需证![]() ……10分
……10分
由题设可知![]() 显然成立,所以
显然成立,所以![]() 得证
……12分
得证
……12分
19已知数列![]() 的通项公式
的通项公式![]() ,记
,记![]() ,试通过计算
,试通过计算![]() 的值,推测出
的值,推测出![]() 的值. (12分)
的值. (12分)
解:![]() , 2分
, 2分
![]() , 4分
, 4分
![]() .8分
.8分
由此猜想,![]() . 12分
. 12分
 20.设动点
20.设动点![]() 到点
到点![]() 和
和![]() 的距离分别为
的距离分别为![]() 和
和![]() ,
,![]() ,且
,且![]() .
.
(1)求证:![]() ;
;
(2)求动点P的轨迹方程. (12分)
解:(1)在![]() 中,
中,![]() ,
,
![]() ,4分
,4分
![]() ,
,
![]() (小于
(小于![]() 的常数) 6分
的常数) 6分
(2)由于![]() ,是小于
,是小于![]() 的常数,
的常数,
故动点![]() 的轨迹
的轨迹![]() 是以
是以![]() ,
,![]() 为焦点,实轴长
为焦点,实轴长![]() 的双曲线.8分
的双曲线.8分
所以,![]() ,
,![]() ,
,![]() , 10 分
, 10 分
所求轨迹方程为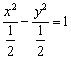 ,即
,即![]() . 12分
. 12分
9. (本小题满分14分)已知直线![]() 与椭圆
与椭圆![]() 相交于A、B两点.
相交于A、B两点.
(1)若椭圆的离心率为![]() ,焦距为2,求线段AB的长;
,焦距为2,求线段AB的长;
(2)在(1)的椭圆中,设椭圆的左焦点为F1,求△ABF1的面积。
19.解:(1)![]()
![]() (3分)
(3分)
∴椭圆的方程为![]() (4分)
(4分)
联立 (5分)
(5分)
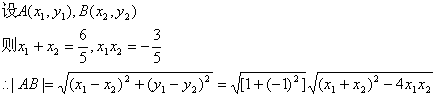 (8分)
(8分)
![]() (10分)
(10分)
(2)由(1)可知椭圆的左焦点坐标为F1(-1,0),直线AB的方程为x+y-1=0,
所以点F1到直线AB的距离d=![]() , (12分)
, (12分)
又AB=![]() , ∴△ABF1的面积S=
, ∴△ABF1的面积S=![]() =
=![]() (14分)
(14分)