安陆一中高二数学同步测试
直线与圆锥曲线(四)
一.选择题
1已知椭圆![]() 的离心率
的离心率![]() ,则实数
,则实数![]() 的值为( )
的值为( )
A,3
B,3或![]() C,
C,![]() D,
D,![]() 或
或![]()
2一动圆与两圆![]() 和
和![]() 都外切,则动圆圆心的轨迹为( )
都外切,则动圆圆心的轨迹为( )
A,圆 B,椭圆 C,双曲线的一支 D,抛物线
3已知双曲线的顶点为![]() 与(2,5),它的一条渐近线与直线
与(2,5),它的一条渐近线与直线![]() 平行,则双曲
平行,则双曲
线的准线方程是( )
A,![]() B,
B,![]() C,
C,![]() D,
D,![]()
4抛物线![]() 上的点P到直线
上的点P到直线![]() 有最短的距离,则P的坐标是( )
有最短的距离,则P的坐标是( )
A,(0,0)
B,![]() C,
C,![]() D,
D,![]()
5已知点F![]() ,直线
,直线![]() :
:![]() ,点B是
,点B是![]() 上的动点.若过B垂直于
上的动点.若过B垂直于![]() 轴的直线与线段
轴的直线与线段
BF的垂直平分线交于点M,则点M的轨迹是( )
A,双曲线 B,椭圆 C,圆 D,抛物线
二.填空题
6椭圆![]()
![]() 上的一点到左焦点的最大距离为8,到右准线的最小距离
上的一点到左焦点的最大距离为8,到右准线的最小距离
为![]() ,则此椭圆的方程为
.
,则此椭圆的方程为
.
7与方程![]() 的图形关于
的图形关于![]() 对称的图形的方程是
.
对称的图形的方程是
.
8设P是抛物线![]() 上的动点,点A的坐标为
上的动点,点A的坐标为![]() ,点M在直线PA上,
,点M在直线PA上,
且分![]() 所成的比为2:1,则点M的轨迹方程是
.
所成的比为2:1,则点M的轨迹方程是
.
9设椭圆与双曲线有共同的焦点![]() ,且椭圆长轴是双曲线实轴的2倍,
,且椭圆长轴是双曲线实轴的2倍,
则椭圆与双曲线的交点轨迹是 .
三.解答题
10已知点H![]() ,点P在
,点P在![]() 轴上,点Q在
轴上,点Q在![]() 轴的正半轴上,点M在直线PQ上,
轴的正半轴上,点M在直线PQ上,
且满足![]() ,
,![]() .
.
(I)当点P在![]() 轴上移动时,求点M的轨迹C;
轴上移动时,求点M的轨迹C;
(II)过点T![]() 作直线
作直线![]() 与轨迹C交于A,B两点,若在
与轨迹C交于A,B两点,若在![]() 轴上存在一点E
轴上存在一点E![]() ,
,
使得![]() 是等边三角形,求
是等边三角形,求![]() 的值.
的值.
11已知双曲线C:![]()
![]() ,点B,F分别是双曲线C的右顶点和右焦点,
,点B,F分别是双曲线C的右顶点和右焦点,
O为坐标原点.点A在![]() 轴正半轴上,且满足
轴正半轴上,且满足![]() 成等比数列,过点F作双曲
成等比数列,过点F作双曲
线C在第一,第三象限的渐近线的垂线![]() ,垂足为P.
,垂足为P.
(I)求证:![]()
![]() ;
(II)设
;
(II)设![]() ,直线
,直线![]() 与双曲线C的左,右两分
与双曲线C的左,右两分
支分别相交于点D,E,求![]() 的值.
的值.
12已知双曲线的两个焦点分别为![]() ,
,![]() ,其中
,其中![]() 又是抛物线
又是抛物线![]() 的焦点,点A
的焦点,点A![]() ,
,
B![]() 在双曲线上.
在双曲线上.
(I)求点![]() 的轨迹方程;
(II)是否存在直线
的轨迹方程;
(II)是否存在直线![]() 与点
与点![]() 的轨迹有且只
的轨迹有且只
有两个公共点?若存在,求实数![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
直线与圆锥曲线(四)参考答案
一.选择题
1 B.
二.填空题
6可得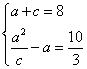 ,消去
,消去![]() ,整理得
,整理得![]() ,有
,有![]() 或
或![]() (舍去),得
(舍去),得![]() ,
,
![]() ,所以所求的椭圆方程为
,所以所求的椭圆方程为![]() .
.
7设点P![]() 是所求曲线上任一点,它关于
是所求曲线上任一点,它关于![]() 对称的点
对称的点![]() 在
在![]() 上,
上,
有![]() ,即
,即![]() .
.
8设点P![]() ,M
,M![]() ,有
,有![]() ,
,![]() ,得
,得![]() ,
,![]()
而![]() ,于是得点M的轨迹方程是
,于是得点M的轨迹方程是![]() .
.
9由条件可得![]() 或
或![]() ,设P
,设P![]() 代入可知交点的轨迹是两个圆.
代入可知交点的轨迹是两个圆.
三.解答题
10解:(I) 设点M![]() ,由
,由![]() ,得P
,得P![]()
由![]() ,得
,得![]() 所以
所以![]() .又点Q在
.又点Q在![]() 轴的正半轴上,得
轴的正半轴上,得![]() .
.
所以,动点M的轨迹C是以(0,0)为顶点,以(1,0)为焦点的抛物线,除去原点.
(II)设直线![]() :
:![]() ,其中
,其中![]() ,代入
,代入![]() ,整理得
,整理得![]() ①
①
设A![]() ,B
,B![]() ,
,![]() ,
,![]()
=![]() ,有AB的中点为
,有AB的中点为![]() ,
,
AB的垂直平分线方程为![]() ,令
,令![]() ,
,![]() ,有E
,有E![]()
由![]() 为正三角形,E到直线AB的距离为
为正三角形,E到直线AB的距离为![]() ,知
,知![]() .
.
由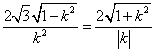 ,解得
,解得![]() ,所以
,所以![]() .
.
11(I)证明:直线![]() 的方程为:
的方程为:![]()
由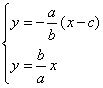 ,得P
,得P![]() ,又
,又![]() 成等差数列,
成等差数列,
得A(![]() ,0),有
,0),有![]() ,
,
于是![]() ,
,![]() ,因此
,因此![]()
![]() .
.
(II)由![]() ,得
,得![]() ,
,![]() :
:![]()
由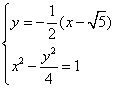 ,消去
,消去![]() ,整理得
,整理得![]() ①
①
设D![]() ,E
,E![]() ,由已知有
,由已知有![]() ,且
,且![]() ,
,![]() 是方程①的两个根.
是方程①的两个根.
![]() ,
,![]() ,
,![]() ,解得
,解得![]() 或
或![]() .
.
又![]() ,得
,得![]() =
=![]() ,因此
,因此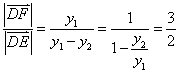 .
.
12解:(I)![]() ,
,![]() ,设
,设![]() 则
则
![]() ,去掉绝对值号有两种情况,分别得
,去掉绝对值号有两种情况,分别得![]() 的轨迹
的轨迹
方程为![]() 和
和![]() (
(![]() )
)
(II)直线![]() :
:![]() ,
,![]() :
:![]() ,D(1,4),椭圆Q:
,D(1,4),椭圆Q:![]()
①若![]() 过点
过点![]() 或D,由
或D,由![]() ,D两点既在直线
,D两点既在直线![]() 上,又在椭圆Q上,但不在
上,又在椭圆Q上,但不在![]() 的轨迹上,
的轨迹上,
知![]() 与
与![]() 的轨迹只有一个公共点,不合题意.
的轨迹只有一个公共点,不合题意.
②若![]() 不过
不过![]() ,D两点(
,D两点(![]() ).则
).则![]() 与
与![]() 必有一个公共点E,且点E不在椭圆Q上,
必有一个公共点E,且点E不在椭圆Q上,
所以要使![]() 与
与![]() 的轨迹有且只有两个公共点,必须使
的轨迹有且只有两个公共点,必须使![]() 与Q有且只有一个公共点,
与Q有且只有一个公共点,
把![]() 代入椭圆的方程并整理得
代入椭圆的方程并整理得![]()
由![]() ,得
,得![]() .
.