安陆一中高二数学同步测试直线与圆锥曲线（七）
一．选择题
1. 直线
到直线
的角是（ ）
A. 
B. 
C. 
D. 
2. 若关于x、y的二次方程
的轨迹存在，则它一定表示（ ）
A. 椭圆与圆 B. 椭圆或双曲线
C. 抛物线 D. 双曲线
3. 椭圆
上有一点P到左准线的距离是2.5，那么P点到右焦点的距离是（ ）
A. 8 B. 
4. 双曲线
的两条准线三等分焦距，则它的离心率是（ ）
A. 
B.
C. 
D. 
5. 抛物线
和圆
上最近两点间的距离是（ ）
A. 
B. 
C. 
D. 
6. 已知双曲线的实轴长为4，AB为左焦点
的弦，
，
为右焦点，则
的周长是（ ）
A. 14 B. 11 C. 5 D.7
7. 已知A、B是抛物线
上两个点，O为坐标原点，若
且抛物线的焦点恰为
的垂心，则直线AB的方程是（ ）
A. 
B.
C. 
D.
二．填空题
8. 椭圆
的焦点为
，点P为其上的动点，当
为钝角时，点P横坐标的取值范围是_________。
9. 中心在原点，一个焦点是
，一条渐近线是直线
的双曲线方程是______
三．解答题
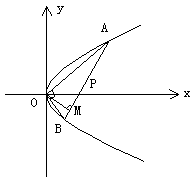
10. 如图，设点A和B为抛物线
上原点以外的两个动点，已知
，
，求点M的轨迹方程，并说明它是什么曲线。
11. （2003年北京春季高考文史类）设A（－c，0），B（c，0）（c>0）为两定点，动点P到A点的距离与B点的距离的比为定值a（a>0），求P点的轨迹。
12. 是否存在同时满足下列条件的双曲线，若存在，求出其方程，若不存在，说明理由。
13. 抛物线y＝x2上不存在关于直线y＝m(x－3)对称的两点，求m的范围。
14. 已知⊙C的圆心在抛物线x2＝2py(p>0)上运动，且⊙C过A（0，p）点，若MN为⊙C在x轴上截得的弦，设AM＝l1，AN＝l2，求式子
15. 已知抛物线y＝(t2＋t＋1)x2－2(a＋t)2x＋t2＋3at＋b，对任意实数t，抛物线总过定点P（1，0），求抛物线与x轴交点的横坐标的取值范围。
16. 如图，直线l1和l2相交于点M，l1⊥l2，点N∈l1，以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等，若ΔAMN为锐角三角形，
AN＝3，且BN＝6，建立适当的坐标系，求曲线段C的方程。
直线与圆锥曲线（七）参考答案
一．选择题
1. C 2. D 3. A 4. D
5. D
提示：圆心（3，0）到抛物线上任一点
的距离：
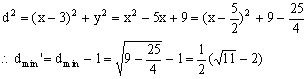
6. A 7. C
二．填空题
8. 
9. 
提示：由题意可设双曲线方程为
即
再由焦点坐标为，解得
三．解答题
10. 解法一：设AB两点为
（
）
由知点O（0，0）在以AB为直径的圆上，
方程：
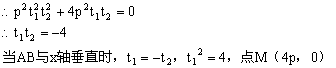
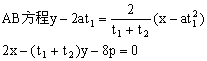
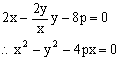
法二：设OA的斜率为k，
设
化简代入即可得方程。
法三：由法二得AB方程，令y＝0，得x＝4p
故AB过定点（4p，0），又
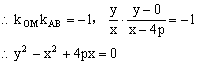
11.解：设动点P的坐标为（x，y）
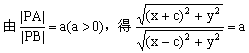
12. 解：假设存在同时满足题中两条件的双曲线。
（1）若双曲线焦点在x轴上
设动点P的坐标为（x，y）
此时存在双曲线方程为
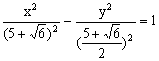
13.解：若m＝0，曲线y＝x2上没有关于直线y＝0对称的两点
若l与抛物线有两交点，则
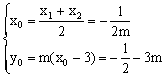
14.解：根据题意，⊙C方程可设为
15.解：∵抛物线过P（1，0）
这个关于t的方程的解集是R
设抛物线与x轴的另一交点为（x，0）
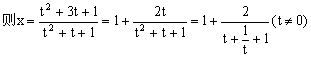
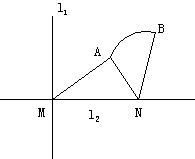
16. 解：如图建立坐标系，以l1为x轴，MN的中垂线为y轴，点O为坐标原点。
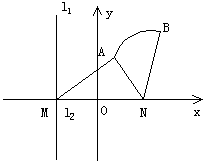
依题意知：曲线段C是以点N为焦点，以l2为准线的抛物线的一部分，其中A、B分别是C的端点。
由点B在曲线段C上
综上得曲线段C的方程为
