高二数学第二学期半期考试题
(时间120分钟 满分150分)
卷I 选择题
一、选择题:(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.点A在直线l上,l在平面![]() 外,用符号表示正确的是 ( )
外,用符号表示正确的是 ( )
A.![]() B.
B. ![]() C.
C.![]() D.
D.![]()
2.以下四个结论:
① 若![]() ,则a, b为异面直线;
,则a, b为异面直线;
② 若![]() ,则a, b为异面直线;
,则a, b为异面直线;
③ 没有公共点的两条直线是平行直线;
④ 两条不平行的直线就一定相交。其中正确答案的个数是( )
A.0个 B.1个 C.2个 D.3个
3.已知P为△ABC所在平面α外一点,PA=PB=PC,则P点在平面![]() 内的射影一定是△ABC的 ( )
内的射影一定是△ABC的 ( )
A、内心 B、外心 C、垂心 D、重心
4.下面叙述正确的是( )
 A.过平面外一点只能作一条直线与这个平面平行;
A.过平面外一点只能作一条直线与这个平面平行;
B.过直线外一点只能作一个平面与这条直线平行;
C.过平面外一点只能作一个平面与这个平面垂直;
D.过直线外一点只能作一个平面与这条直线垂直.
5.(如右图)正方体ABCD-A1B
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
6.一条直线和两异面直线b,c都相交,则它们可以确定( )
A.一个平面 B.两个平面 C.三个平面 D.四个平面
7.(理)三位同学分别从“计算机”及“英语口语”两项活动中选修一项,不同的选法有 种。 ( )
A.
5 B.
(文)直线a与平面![]() 所成的角为30o,直线b在平面
所成的角为30o,直线b在平面![]() 内,若直线a与b所成的角为
内,若直线a与b所成的角为![]() ,则 ( )
,则 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.一个简单多面体的各面都是三角形,且有6个顶点,则此简单多面体的面数是( )
A.
4 B.
9.有共同底边的等边三角形![]() 和
和![]() 所在平面互相垂直,则异面直线
所在平面互相垂直,则异面直线![]() 和
和![]() 所成角的余弦值为 ( )
所成角的余弦值为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.(理) 在北纬45°的纬度圈上有甲、乙两地,两地经度差为90°,则甲、乙两地的球面距离为(设地球半径为R)( )
A. ![]() B.
B. ![]() C.
C.
![]() D.
D.
![]()
(文)已知三个平面![]() 、
、![]() 、
、![]() 相交于点O,且
相交于点O,且![]() ,则交线OA与平面OBC所成的角的余弦值是( )
,则交线OA与平面OBC所成的角的余弦值是( )
A.![]() B.
B.![]() C.
C. ![]() D.
D.![]()
11.一个棱锥被平行于底面的平面所截,若截面面积与底面面积之比为1:2,则此棱锥的高被分成两段之比(自上而下)为( )
A.
1:2 B.
1:![]() +1) D. 1:(
+1) D. 1:(![]() )
)
12.正方体![]() 中截面
中截面![]() 和截面
和截面![]() 所成的二面角的大小为( )
所成的二面角的大小为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
卷II 主观题
二.填空题(本大题4小题,每小题5分,共20分)
13.(理)球的两个平行截面面积分别为5π和8π,且在球心的同侧,这两个截面间的距离等于1,则球的半径为 ;
(文)在长方体ABCD-A1B
14.正四面体V—ABC的棱长为![]() ,E,F,G,H分别是VA,VB,
,E,F,G,H分别是VA,VB,
BC,AC的中点,则四边形EFGH面积是__________ 。
 15.如图,
15.如图,![]() 是边长为
是边长为![]() 的正方形,
的正方形,![]() 和
和![]() 都与平面
都与平面![]() 垂直,且
垂直,且![]() ,设平面
,设平面![]() 与平面
与平面![]() 所成二面角为
所成二面角为![]() ,则
,则![]() ;
;
16.已知m、n是不同的直线,![]() 、
、![]() 是不重合的平面, 给出下列命题:
是不重合的平面, 给出下列命题:
①若![]() ,则
,则![]() ;②若
;②若![]() ,则
,则![]() ;
;
③若![]() ,则
,则![]() ; ④
; ④![]() 、
、![]() 是一对异面直线且
是一对异面直线且![]() , 若
, 若![]() ,则
,则![]() ,其中,真命题的编号是 .
,其中,真命题的编号是 .
 三、解答题:(6个小题,共70分)
三、解答题:(6个小题,共70分)
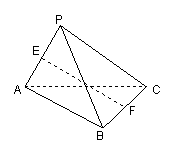
17.(本小题满分10分)已知ABCD是正方形,PA⊥平面ABCD,且PA=AB=2,E、F是侧棱PD、PC的中点。
(1)求证:![]() 平面PAB ;
平面PAB ;
(2)求直线PC与底面ABCD所成角![]() 的正切值。
的正切值。
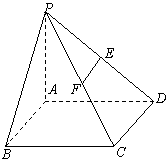
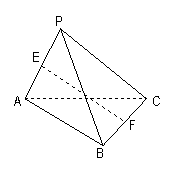
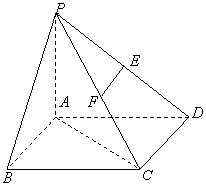
18、(本小题满分12分)已知P为△ABC所在平面外的一点,PC⊥AB,PC=AB=2,E、F分别为PA和BC的中点;
(1)求EF与PC所成的角;
(2)求线段EF的长
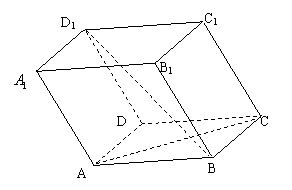
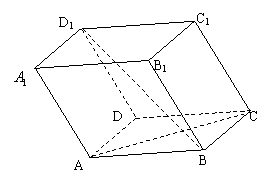 19.(本小题满分12分)已知平行六面体
19.(本小题满分12分)已知平行六面体![]() ,各条棱长均为
,各条棱长均为![]() ,底面是正方形,且
,底面是正方形,且![]() ,设
,设![]() ,
,![]() ,
,![]() ,
,
(1)用![]() 、
、![]() 、
、![]() 表示
表示![]() 及求
及求![]() ;
;
(2)求异面直线![]() 与
与![]() 所成的角
所成的角
的余弦值。
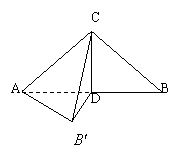
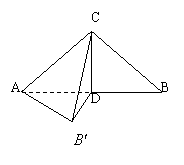 20. (本题满分12分)以等腰直角三角形ABC(
20. (本题满分12分)以等腰直角三角形ABC(![]() )的斜边AB上的高CD为棱折成一个
)的斜边AB上的高CD为棱折成一个![]() 的二面角,使
的二面角,使![]() 到
到![]() 的位置,已知斜边AB=2,求:
的位置,已知斜边AB=2,求:
(1)C到平面![]() 的距离 ;
的距离 ;
(2)A到平面![]() 的距离 ;
的距离 ;
(3)AC与平面![]() 所成的角。
所成的角。
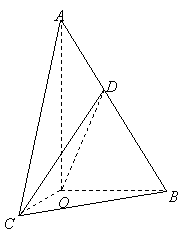
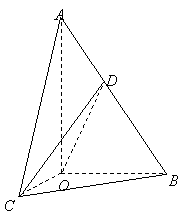 21.(本小题满分12分)如图,在
21.(本小题满分12分)如图,在![]() 中,
中,![]() ,斜边
,斜边![]() .
.![]() 可以通过
可以通过![]() 以直线
以直线![]() 为轴旋转得到,且二面角
为轴旋转得到,且二面角![]() 是直二面角.动点
是直二面角.动点![]() 在斜边
在斜边![]() 上.
上.
(文、理)(1)求证:平面![]() 平面
平面![]() ;
;
(文、理)(2)当![]() 为
为![]() 的中点时,求异面直
的中点时,求异面直
线![]() 与
与![]() 所成角的大小;
所成角的大小;
(理)(3)求![]() 与平面
与平面![]() 所成角的最大值.
所成角的最大值.
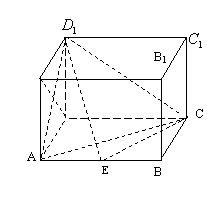
22.(本题满分12分)如图,在长方体ABCD—A1B
(文、理)(1)证明:D1E⊥A1D;
(文、理)(2)当E为AB的中点时,求点E到面ACD1的距离;
(理)(3)当AE等于何值时,二面角D1—EC-D的大小为![]() .
.
![]()
![]()
![]()
 第二卷(答题卡)
第二卷(答题卡)
一、单选题(每小题5分,共60分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题(每小题5分,共20分,请把正确的答案写在相应的横线上。)
13、__________________; 14、___________________;
15、 __________________; 16、 ___________________;
 三、解答题:(共70分,解答应写出文字说明、证明过程或演算步骤)
三、解答题:(共70分,解答应写出文字说明、证明过程或演算步骤)
17.
18.
 19.
19.
 |
20.
![]()

 21.
21.
![]()
![]()
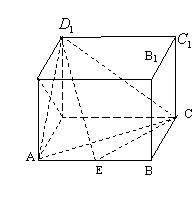 22.
22.
试题参考解答
一、选择题: BABDD BCCBB DD
二、填空题:
13、(理)3;(文)![]() 14.
14. ![]() 15.
15.![]() 16.③④
16.③④
三、解答题:
17、解:证明:(1)
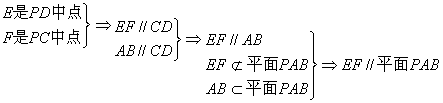 |
证明:(2)连结AC,因为PA![]() 平面ABCD,所以
平面ABCD,所以![]() 就为直线PC与平面ABCD所成的角
就为直线PC与平面ABCD所成的角![]() 。即
。即![]()
又因为正方形ABCD的边长为2,所以AC=![]() ,
,
所以![]()
18、解:设PB的中点为G,连接FG,EG,
则FG∥PC且FG=![]() PC,EG∥AB且EG=
PC,EG∥AB且EG=![]() AB
AB
故∠GFE为EF与PC所成的角,∠EGF为PC与AB所成的角
∵ PC⊥AB
∴ ∠EGF=90° 又EG=GF=1
∴ ∠GFE=45° EF=![]()
19.解:(1)![]()
![]() ……2分
……2分
![]()
![]() ……2分
……2分
![]()
![]() ……2分
……2分
(2)![]()
![]() ……2分
……2分
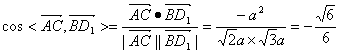 ……1分
……1分
![]() 异面直线
异面直线![]() 与
与![]() 所成的角的余弦值是
所成的角的余弦值是![]() 。 ……1分
。 ……1分
20.(1)![]() ,它们的位置关系在折叠前后不变,
,它们的位置关系在折叠前后不变,![]() 平面
平面![]() ,CD的长就是C到平面
,CD的长就是C到平面![]() 的距离,CD=1;
的距离,CD=1;
(2)过点A作![]() 交
交![]() 于E,
于E,![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴AE的长为点A到平面
,∴AE的长为点A到平面![]() 的距离,
的距离,![]()
(3)连CE,![]() 平面
平面![]() ,CE为AC在平面
,CE为AC在平面![]() 上的射影,
上的射影,![]() 为
为![]() 与平面所成的角,在
与平面所成的角,在![]() 中,易求得
中,易求得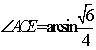
21.(1)略;(2)arctan![]() ;(3)arctan
;(3)arctan![]()
22、解法一(1)∵AE⊥平面AA1DD1,A1D⊥AD1,∴D1E⊥A1D.
(2)设点E到面ACD1的距离为h,在△ACD1中,AC=CD1=![]() ,AD1=
,AD1=![]() ,
,
故![]()
![]()
(3)过D作DH⊥CE于H,连D1H、DE,则D1H⊥CE,∴∠DHD1为二面角D1—EC—D的平面角.设AE=x,则BE=2-x,
![]()
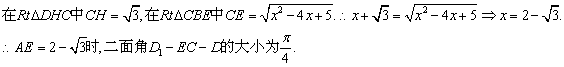 解法二以D为坐标原点,直线DA,DC,DD1分别为x,y,z轴,建立空间直角坐标系,设AE=x,则A1(1,0,1),D1(0,0,1),E(1,x,0),A(1,0,0)C(0,2,0)
解法二以D为坐标原点,直线DA,DC,DD1分别为x,y,z轴,建立空间直角坐标系,设AE=x,则A1(1,0,1),D1(0,0,1),E(1,x,0),A(1,0,0)C(0,2,0)
(1)![]() 即DA1⊥D1E.
即DA1⊥D1E.
(2)因为E为AB的中点,则![]() ,
,![]()
设平面ACD1的法向量为![]() ,则
,则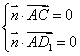 ,即
,即![]() 得
得![]()
从而![]() ,所以点E到平面AD
,所以点E到平面AD![]()
(3)设平面D1EC的法向量![]() ,∴
,∴![]()
由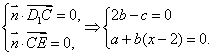 令b=1, ∴c=2,a=2-x,∴
令b=1, ∴c=2,a=2-x,∴![]() 依题意
依题意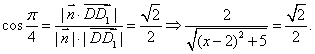 ∴
∴![]() (不合,舍去),
(不合,舍去),
![]() ∴AE=
∴AE=![]() 时,二面角D1—EC—D的大小为
时,二面角D1—EC—D的大小为![]() .
.