高二数学第二学期第三次考试
数 学 试 题
命题人：宋 磊 审核人：周希银
YCY命题 命命提
试卷分第Ⅰ卷（填空题）和第Ⅱ卷（解答题）两部分，满分160分，考试时间120分钟.
第Ⅰ卷 (填空题 共7０分)
一、填空题：（本大题共14小题，每小题5分，共70分，将正确答案写在答案卡上）
1．
=_______________.
2．已知向量
，则
=
3．与向量
平行的单位向量是
4．已知向量
，若
平行，则
=
5．已知向量
是不平行
轴的单位向量，且
，则
6．在三角形
中，若
，则
=
7．化简：
8．使函数
是减函数，
是增函数的角的取值范围是
9．将函数
的图象沿轴向右平移
个单位，再保持图象上纵坐标不变，横坐标变为原来的2倍，得到的曲线与的图象相同，则
10．函数
的单调递减区间是
11．已知函数是R上的奇函数，则函数
的图象经过的定点为
12．函数
对一切实数都满足
，且
有3个实根，则这3个实根之和为
13．集合
，若
，则
14．已知集合
，若
则实数
第Ⅱ卷 (解答题 共90分)
二、解答题（解答给出必要的文字说明和演算步骤）
15.（本小题满分14分）
已知函数
在区间
上有最小值，记作
（1）求的函数表达式； （2）求的最大值。
（答案请写在答题纸上）
16．（本小题满分14分）
已知函数
（1）当
时，函数恒有意义，求实数
的取值范围；
（2）是否存在这样的实数，使得函数在区间
上为减函数，并且最大值为1？如果存在，试求出的值；如果不存在，请说明理由。
（答案请写在答题纸上）
17．（本小题满分15分）
已知向量
，定义
（1）求函数的最小正周期；
（2）若
，当
时，求取值范围。
（答案请写在答题纸上）
18．（本小题满分15分）
在
中，
分别是角A，B，C的对边，且
（1）求角B的大小。
（2）若
，求的面积。
（答案请写在答题纸上）
19．（本小题满分16分）
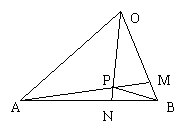在
的边
上分别取点
，使
，
，设线段AM与ON交于点P，记
（1）若
，求
值。
（2）用
表示向量
。
（答案请写在答题纸上）
20．（本小题满分16分）
已知点
，试用向量方法
（1）
求
（2）
求
与
的交点
的坐标。
（答案请写在答题纸上）