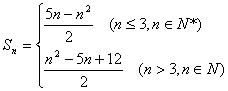高二数学第二学期阶段测试
必修五专题检测
一、填空题
1．在△ABC中，角
均为锐角，且
则△ABC的形状是钝角三角形。
2．在△
中，若
，则
等于
。
3．等差数列
项的和
等于99。
4．在公比为整数的等比数列
中，如果
那么该数列的前
项之和为
。
5．若
，则
等于3 。
6．若
，则函数
的值域是
7．下列不等式（1）
（2）
（3）
（4）
，其中不能恒成立的
是（1）（2）（4）。
8．二次方程
,有一个根比
大,另一个根比
小,则
的取值范围是
9．一个两位数的个位数字比十位数字大
，若这个两位数不大于
，则这个两位数为13或24。
10．函数
的最大值为1。
11．在△ABC中，
，则
的最大值是4 。
12．在
△ABC中，
，则
的最大值是
。
13．两个等差数列
则
=
14．在等比数列中, 若
则
=
三、解答题
15 ．⑴在△ABC中， 
，求
。
⑵在△ABC中，设
求
的值。
解析：（1）
，
而
，所以
（2）∵
∴
，即
，
∴
，而
∴
，
∴
16．已知
、
满足约束条件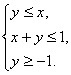
（1）求
的最小值，以及相应的、值；
（2）求
的最大值，以及相应的、值
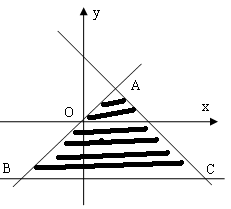
解析：作出区域如右图
（1）直线经过点
时，有最小值3
（2）
，其中点
为三角形ABC内部及其边界上的点，可知当点P与点C重合时，
17．已知数列的前
项和
，
（1）求
的值。 （2）求
的表达式
解析： （1）
=
；
；
∴
（2）为偶数时
；
为奇数时
∴
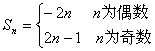
18。某食品厂定期购买面粉，已知该厂每天需要面粉6吨，每吨面粉的价格为1800元，面粉的保管等其它费用为平均每吨每天3元，购面粉每次需支付运费900元．求该厂多少天购买一次面粉，才能使平均每天所支付的总费用最少？
解析：设该厂天购买一次面粉，平均每天所支付的总费用为元．
∴购买面粉的费用为
元，
保管等其它费用为
，
∴
，即当
，即
时，有最小值
，
答：该厂
天购买一次面粉，才能使平均每天所支付的总费用最少．
19．已知二次函数
的图像经过坐标原点，其导函数为
，数列
的前n项和为
，点
均在函数的图像上。
（1）求数列的通项公式；
（2）设
，
是数列
的前n项和，求使得
对所有
都成立的最小正整数m；
解析：（1）设这二次函数f(x)＝ax2+bx (a≠0) ,则 f`(x)=2ax+b,由于f`(x)=6x－2,得
a=3 , b=－2, 所以 f(x)＝3x2－2x.
又因为点均在函数的图像上，所以＝3n2－2n.
当n≥2时，an＝Sn－Sn－1＝（3n2－2n）－
＝6n－5.
当n＝1时，a1＝S1＝3×12－2＝6×1－5，所以，an＝6n－5 （）
（2）由（1）得知
＝
＝
，
故Tn＝
＝
＝（1－
）.
因此，要使（1－）<
（）成立的m,必须且仅须满足≤，即m≥10，所以满足要求的最小正整数m为10.
20。已知数列中，
，
且
（1）求数列的通项公式；
（2）设函数
，数列的前项和为
，求的通项公式；
（3）求数列
的前项和。
解析：（1）∵
∴
∴
， 累乘，得
。
（2）
∴
当
时，
时，
也符合
∴的通项公式是
（3）数列是首项为
，公差
的等差数列
当
，即
时，
；
当
时，
=
综上所述，