高二下期中（理科）数学试题
命题：何胜明
一，选择题（共10小题，每小题5 分，共计50分）
1，设M={菱形}，N={矩形}，则
A, 
， B, {矩形}
， C, {矩形或菱形}， D, {正方形}，
2，不等式
的解集是
A.
B.(－3,
) C.
D．
3，数列3，5，9，17，33，65,………的通项公式
等于
A．
B．
C．
D．
4，过点
且和圆
相切的直线方程是
A.
B.
C.
D.
5，已知
A．0 B．
C．－ D．－
6，
2009 =
A．1 B．－
D．－
7，椭圆
上的点P到它的左准线的距离是10，那么点P 到它的右焦点的距
离是
A
12
D 15
8，甲、乙两人各抛掷一枚各面分别标有1、2、3、4、5、6的正方体骰子，；向上的点数分别为
、
，则点P（，）落在园2+2=16内部的概率为
A, 
; B,
C, 
D, 
9，设函数
，则
的解集是
A．
B． 
C．
D．
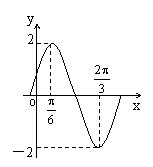10，函数y＝Asin(ωx＋φ) (A＞0，ω＞0，φ＜
）的图象
如图所示，则y的表达式为
A，y＝2sin(
) B，y＝2sin(
)
C，y＝2sin(2x＋
) D，y＝2sin(2x－)
二，填空题（共4 小题，每小题5 分，共计20分）
11，已知
的展开式中
的系数与
的展开式中x3的系数相等，
则
= .
12，圆心在点C（2，
）且半径R=2的圆的极坐标方程为
，
13，一个正方体的所有棱长都是1，八个顶点在同一个球面上，则此球的表面
积为 ．
14，若X～N(2,1), 求P(3＜x＜5) = ,
（参考数据： P(
－
＜X＜+) = 0.6826, P(－2＜X＜+2) =0.9544
P(－3＜X＜+3) = 0.9974 ）
三，解答题（共6大题，共计80分），
15， （12分）在△
中，角
所对的边分别为
，
．
（1）,试判断△的形状；
（2）,若△的周长为16，求面积的最大值．
16，（12分）一个口袋中装有大小相同的2个白球和4个黑球．
（1）,采取放回抽样方式，从中摸出两个球，求两球恰好颜色不同的概率；
（2）,采取不放回抽样方式，从中摸出两个球，求摸得白球的个数x的概率分布列和期望
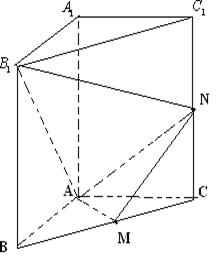
17，（14分）直三棱柱ABC—
中，侧棱CC1 = 2， ∠BAC = 90°，
，M是棱BC的中点，
N是CC1中点，求
（1）,二面角B1—AN—M的余弦函数值；
（2）,C1到平面AMN的距离.
18，（14分）已知双曲线方程为：
，又已知两点P（8，1），Q（2，1）；
（1），过点P作直线交双曲线于A、B两点，且点P恰为线段AB的中点，求直线
AB方程；
（2），是否存在过点Q的直线
交双曲线于C、D两点，且点Q恰为线段CD的中点？
若存在，求方程；若不存在，则说明理由，
19，（14分）已知数列
中，
=2，且
=3
+2，
（1），求数列的通项公式；
（2），若数列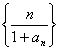
的前n项和为
，求的表达式；
20，（14分）若函数f(x)
=2 ln (x－3) －
,
(1),求函数f(x)的单调递增区间；
(2),若关于x的方程f(x)
+－7x－a =0在区间
[4, 6] 内恰有两个相异实根，
求实数a的取值范围；
华侨城中学2007---2008学年下学期高二期中考试题 （
（理科）答案：
一，1，D, 2，D． 3，B 4，A ； 5，C
6，D 7，C 8， B ； 9， B． 10，C
二， 11，
; 12， 
=4 cos(
－),
13， 3
14， 0.1574,
三，15，解：(1)、
…………4分
所以此三角形为直角三角形. …………6分
(2)．
…………9分
当且仅当
时取等号，
此时面积的最大值为
．
…………12分
16，解：
（Ⅰ）解法一：“有放回摸两次，颜色不同”指“先白再黑”或“先黑再白”，
设事件
： “有放回摸球两次，两球恰好颜色不同”
……………………2分
∵“两球恰好颜色不同”共
种可能，
……………………5分
∴
． ……………………………7分
解法二：“有放回摸取”可看作独立重复实验， ………………………2分
∵每次摸出一球得白球的概率为
．
…………………4分
∴“有放回摸两次，颜色不同”的概率为
……………6分．
（Ⅱ）设摸得白球的个数为x，依题意得：
，
，
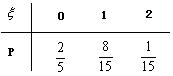…………10分
∴
，
………………12分
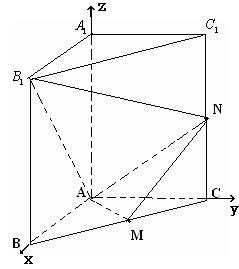17，（1）建立坐标系如图所示，则
设平面AMN的法向量为
，平面AB1N的
法向量为
…………………………2分
由
，
得
，
令
，则
，
于是
…………………………3分
由
，得
，
令
，则
，于是
……………………………5分
…………6分
………………………………………………8分
（2）
，C1 到平面AMN的距离：
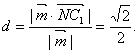………14分
18，（1），解法一：
设直线AB：
（t---参数），
……2分
代入得：
（cos
－4sin）t2 +
(16cos－8sin)t +
56=0, ……4分
由于点P为AB中点，所以t
1+t2=0，得2 cos=
sin，……6分
∴ K=tan=2, ∴直线AB方程为 y－1=2(x-8), 即2x－y－15=0; ……8分
解法二：设点A（x1， y1）、B（x2 ，y2），则有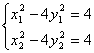
……3分
相减得
，
∴4
=
，
∴
= 
=
= 2，
……6分
∴ AB方程为：y－1= 2(x-8), 即2x－y－15=0; ……8分
（2），若存在过点Q的直线满足条件，
设点C（x3， y3）、D（x4 ，y4），则有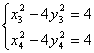
， ……10分
相减得
，
∴
= 
=
=
，
∴ CD方程为：y－1= (x－2), 即x=2y; ……12分
由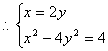
Þ 4y2－4y2=4,
Þ 0=4 ，矛盾，
∴ 不存在过点Q的直线满足条件，
……14分
19，解：（1），由=3+2可得：+1=3（+1）； ……2分
∴有
=3 （常数）， ……4分
∴数列
是等比数列，且首顶为+1=3，公比为
=3，
则 +1=3×
=
，则=－1； ……6分
（2）由
= 
;
∴ = 
------------① ……8分
3 = 1+
+ -------- + 
------------② ……10分
②－①：
2 = 1+
-------+
……12分
= 
－ = 
∴ = 
……14分
20，（1）， x－3＞ 0, 得定义域：(3，+∞)， ……1分
(x)=
－2(x－3), 令(x)=0，得根x=4，x=2（舍）， ……3分
……………………6分
∴f(x)的单调增区间是 (3,4)， ……7分
(2), 2 ln (x－3) －x－9－a=0,
设函数g(x)=
2 ln (x－3) －x－9－a, 
=－1. ……9分
令=0，得x=5,
∴函数g(x)在区间(4,5) ↑,在区间(5,6) ↓， ……10分
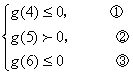
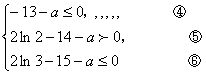……13分
∴ 实数a的取值范围是: 
;
……14分