高二数学(文科)中段考试题
说明:1.试卷满分150分,考试时间120分钟.
2.选择题选项涂在答题卡上，填空题和解答题答案写在试卷纸上。
一、选择题（10×5分＝50分）
1、设
，
，
，
，则
（ *** ）。
A．{1，4} B．{1，6} C．{4，6} D．{1，4，6}
2、为研究变量
和
的线性相关性，甲、乙二人分别作了研究，利用线性回归方法得到回归直线方程
和
，两人计算知
相同，
也相同，下列正确的是(***)
A． 与重合
B. 与一定平行
C. 与相交于点
D. 无法判断和是否相交
3、
是两个非空集合，定义
@
=
，若
，
，则@中元素的个数（ *** ）
A. 3个 B. 4 C. 9 D. 12
4、有一段演绎推理是这样的：“直线
平面
，直线
平面，若直线
∥平面，则直线∥直线
”.该结论显然是错误的，这是因为 （ *** ）
A．大前提错误 B.小前提错误 C.推理形式错误 D.非以上错误
5、分析法证明不等式的推理过程是寻求使不等式成立的（ *** ）
A．必要条件； B．充分条件； C．充要条件； D．必要条件或充分条件
6、已知
且
，则
不能是（***）
A．
B．
C．
D．
7、
则集合
中的元素个数（ *** ）
A. 1个 B. 2个 C. 3个 D. 无穷多个
8、已知
，则在下列区间中，
有实数解的是（ *** ）．
A．（－3，－2） B.（－1，0） C. （2，3） D.（4，5）
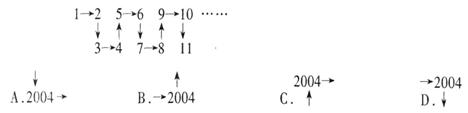
9、把正整数按下图所示的规律排序，则从2003到2005的箭头方向依次为（ B ）
10、我们把1，3，6，10，15，……这些数叫做三角形数，因为这些数目的点子可以排成一个正三角形（如下图）。试求第七个三角形数是（***）
 |
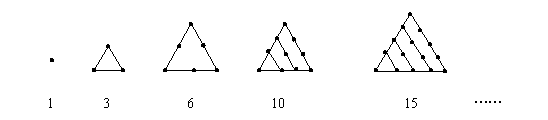A、27 B、28 C、29 D、30
二、填空题（4×5分＝20分）
11、若复数(m2－3m－4)＋(m2－5m－6)
是虚数，则实数m满足 m≠－1且m≠6 .
12、偶函数
在
，
上是增函数，且
，则不等式
的解集是 {xx＜－4，或0＜x＜4} 。
13、观察1=1，1+3=4，1+3+5=9，1+3+5+7=16，……，猜想其一般规律是
1＋3＋5＋7＋…＋（2n—1）＝n2 。
| 规格类型 钢板类型 | A规格 | B规格 |
| 第一种钢板 | 2 | 1 |
| 第二种钢板 | 1 | 3 |
14、将大小不同的两种钢板截成A、B两种规格的成品，每张钢板可同时截得这两种规格的成品的块数如右表所示．现在需要A、B两种规格的成品分别为12块和10块，则至少需要这两种钢板共 7 张．
三、解答题（共6大题，80分）
15、(12分)解不等式
。
解：不等式等价于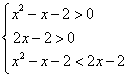
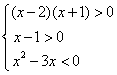
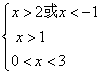
∴不等式的解为
16、(12分)某高校调查询问了56名男女大学生，在课余时间是否参加运动，得到下表所示的数据。从表中数据分析，有多大把握认为大学生的性别与参加运动之间有关系。（8分）
| 参加运动 | 不参加运动 | 合计 | |
| 男大学生 | 20 | 8 | 28 |
| 女大学生 | 12 | 16 | 28 |
| 合计 | 32 | 24 | 56 |
参考数据：
|
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
解：设性别与参加体育运动无关，
∵a＝20，b＝8，c＝12，d＝16，a＋b＝28，a＋c＝32，c＋d＝28，b＋d＝24，n＝56，
∴
的观测值为
∵P(
)＝0.05＝5%,∴有95%把握认为性别与参加运动有关。
17、(14分)若
均为实数，且
。
求证：a，b，c中至少有一个大于0.
解：假设a，b，c都不大于0，则a≤0，b≤0，c≤0。即
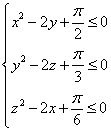
显然错误。
∴“假设a，b，c都不大于0”是错误的，∴a，b，c中至少有一个大于0。
18、(14分)用清水漂洗衣服，若每次能洗去污垢的
，写出存留污垢与漂洗次数的函数关系式，若使存留的污垢不超过原有的1%,则至少要漂洗几次？（
，
）
解：设原来的污垢是a，至少要漂洗x次，
∵每次能洗去污垢的，∴每次漂洗后存留污垢为原来的
，
∴
∴
，
∴至少要漂洗4次, 才能使存留的污垢不超过原有的1%.
19、(14分)已知函数
。（1）求的定义域与值域；
（2）判断的奇偶性并给出证明；（3）判断并证明的单调性。
解：（1）
，
∴的定义域是
∵
，∴的值域是R。
（2）∵的定义域是，
且
∴是奇函数。
（3）是增函数
20、(14分)在各项为正的数列
中，数列的前n项和
满足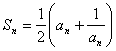
（1） 求
；（2） 由（1）猜想数列的通项公式；（3） 求
答案：（1）
；(2)
；(3)