08年高二数学（理）下学期期中考试试卷
命题人：刘三贵 审题人：熊荣辉
一、选择题（每小题5分，共60分）
1、将4套不同的教学仪器分给3所学校，每校至少一套，不同的分配方案种数为（ ）
A、36 B、
2、若
展开式的二项式系数之和为64，则展开式的常数项为（
）
A、10 B、20 C、30 D、120
3、从1，2，3，……9这九个数中，随机取3个不同的数，则这三个数之和为偶数的概率（ ）
A、
B、
C、
D、
4、设
，如果
，则n和p分别为（ ）
A、18和
B、16和
C、20和
D、15和
5、已知
则
（ ）
A、
B、
(4)－(2)
C、(－4) －(－2) D、(2)－(4)
6、若n为正奇数，则
被9除所得余数是（ ）
A、0 B、3 C、－2 D、8
7、设集合A={1，2，3，4}，m、n∈A，则方程
表示焦点位于x轴上的椭圆有（
）
A、6个 B、8个 C、12个 D、16个
8、如果
的展开式中含有非零常数，则正整数n的最小值为（
）
A、3 B、5 C、6 D、10
9、要从10名女生和5名男生中，选出6名学生组成课外学习小组，如果按性别比例分层随机抽样，试问组成此课外学习小组的概率为（ ）
A、
B、
C、
D、
10、将三种作物种植在如图5块试验田里，每块种植一种作物， 且同一种作物种在相邻的试验田中，不同的种植方法有（ ）
A、24种 B、36种 C、42种 D、48种
11、已知抛物线y=ax2+bx+2(a≠0)的对称轴在y轴的左侧，其中a,b∈{－2,－1,0,1,2}在这些抛物线中，记随机变量
的取值”，则概率
应为（ ）
A、
B、 C、 D、
12、集合A={(x,y)y≥x－1}, B={(x,y)y≤－x+5}，先后掷两颗骰子，设第一颗骰子得点数为a，第二颗骰子得点数为b，则(a,b)∈A∩B的概率为（ ）
A、 B、 C、
D、
二、填空题（每小题4分，共16分）
13、计算
的值
14、随机变量
的分布列如下：
|
| －1 | 0 | 1 |
| p | a | b | c |
其中a、b、c成等差数列，若
，则D=
15、已知(1+x)+(1+x)2+…+(1+x)8=a0+a1x+…+a8x8，则a1+a2+…+a8=
16、在等差数列{an}中，a4=2，a7=－4，现从{an}的前 10项中随机取数，每次取出一个，取后放回，连续抽取3次，假定每次取数互不影响，那么在这些取数中，取出的数恰好为两个正数和一个负数的概率
三、解答题（共74分）
17、（12分）5名男生4名女生排成一排
（1）女生必须站在一起的排法有多少种
（2）男女相间的排法有多少种
（3）甲男生不站排头，乙女生不站排尾的排法有多少种
18、（12分）甲、乙两人独立解某一道数学题，已知甲独立解出的概率为0.6，乙独立解出的概率是0.8
（1）求两人中只有一人解出该题的概率
（2）求两人中至少有一个人解出该题的概率
19、（12分）已知某种从太空飞船中带回的植物种子每粒成功发芽的概率都为，某植物研究所分两个小组分别独立开展该种子的发芽实验，每次实验种一粒种子，假定某次实验种子发芽则称该次实验是成功的，如果种子没有发芽，则称该次实验是失败的。
（1）第一小组做了三次实验，求至少两次实验成功的概率
（2）第二小组进行试验，到成功了4次为止，求在第四次成功之前共有三次失败，且恰有两次连续失败的概率
20、（12分）某项选拔共有三轮考核，每轮设有一问题，能正确回答问题者进入下一轮考核，否则即被淘汰，已知某选手能正确回答第一、二、三轮的问题的概率分别为
，且各轮问题能否正确回答互不影响。
（1）求该选手被淘汰的概率
（2）该选手在选择中回答问题的个数记为ξ，求随机变量ξ的分布列与数学期望
21、（12分）一盒子装有六张卡片，上面分别写着如下六个定义域为R的函数
f1(x)=x,f2(x)=x2,f3(x)=x3,f4(x)=sinx,f5(x)=cosx,f6(x)=x
（1）现从盒子中任取两张卡片，将卡片上的函数相加得一个新函数，求所得函数是奇函数的概率
（2）现从盒子中进行逐一抽取卡片，且每次取出后均不放回，若取到一张记有偶函数卡片则停止抽取，否则继续进行，求抽取次数ξ的分布列和数学期望
22、（14分）如图，四棱锥S—ABCD的所有棱长均为1米，一只小虫从S点出发沿四棱锥爬行，若在每顶点处选择不同的棱都是等可能的，设小虫爬行n米后恰回到S点的概率为Pn.
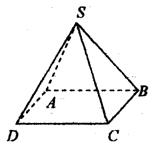（1）求P2，P3的值
（2）求证：3Pn+1+Pn=1(n≥2，n∈N)
（3）求证：P2+P3+…+Pn＞
答 题 卡
一、选择题（每小题5分，共60分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题（每小题4分，共4小题，共16分）
13、 14、 15、 16、
三、解答题（共6小题，其中17~21题每题12分，22题14分，共74分）
17、（12分）
18、（12分）
19、（12分）
20、（12分）
21、（12分）
22、（14分）
宜春中学2007~2008学年度下学期高二年级期中考试数学
参考答案
一、选择题（每小题5分，共60分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | A | B | C | A | B | D | A | B | A | B | D | B |
二、填空题（每小题4分，共4小题，共16分）
13、31 14、
15、502 16、
三、解答题（共6小题，其中17~21题每题12分，22题14分，共74分）
17、（1）女生排在一起的排法，
种………………4分
（2）男女相间的排法，
种…………………………8分
（3）甲不站头，乙不站尾的排法：
种…………12分
18、设甲、乙分别解出此题的事件中为A、B
（1）则只有一人解出的概率P1=
…………6分
（2）至少有一人解出的概率P2=1－P（
）=1－0.4×0.2=0.92…………12分
19、（1）第一小组做了三次实验，至少两次实验成功的概率是
…………6分
（2）第二小组在第4次成功前，共进行了6次试验，其中三次成功三次失败，且恰有两次连续失败，其各种可能的情况种数为12，因此所求的概率为
……………………12分
20、（1）记“该选手能正确回答第i轮的问题”的事件为A1（i=1,2,3），
则P（A1）=
∴该选手被淘汰的概率：
…………6分
（2）ξ的可能值为1，2，3，P(ξ=1)=P
=，
P(ξ=2)=P
P(ξ=3)=P
………………9分
∴ξ的分布列为
|
| 1 | 2 | 3 |
| p |
|
|
|
∴Eξ=1×
……………………12分
21、（1）计事件A为“任取两张卡片，将卡片上的函数相加得到的函数是奇函数”，
所以
……………………4分
（2）ξ可取1，2，3，4
，
……………8分
故ξ的分布列为
|
| 1 | 2 | 3 | 4 |
| p |
|
|
|
|
答：ξ的数学期望为
………………12分
22、（1）P2表示从S点到A（或B、C、D），然后再回到S点的概率
所以
因为从S点沿一棱，不妨设为SA棱再经过B或D，然后再回到S点的概率为
，所以
……………………4分
（2）设小虫爬行n米后恰回到S点的概率为Pn，那么1－Pn表示爬行n米后恰好没回到S点的概率
则此时小虫必在A（或B、C、D）点，所以
，
即
……………………8分
（3）由3Pn+1+Pn=1得
，从而
………10分
所以
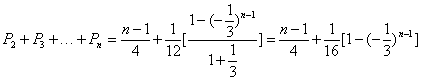
………………14分