08年高二数学五月段考题
姓名__________ 学号_________ 分数___________
一．选择题 （每小题５分，共50分）
1. 若直线a⊥b，且a∥平面α，则直线b与平面α的位置关系是
A.b
α
B.b∥α
C.bα或b∥α D.b与α相交或b∥α或bα都有可能
2. 空间四边形ABCD中，若AB=AD，CB=CD，则AC与BD所成的角为
A.60° B.30° C.45° D.90°
3. 已知P为平面a外一点，直线l
a,点Q∈l,记点P到平面a的距离为a,点P到直线l的距离为b，点P、Q之间的距离为c，则
A.
B.c
C.
D.
4. 已知直线a和平面
、
，∩=l，a
，a，a在、内的射影分别为直线b和c，则b、c的位置关系是
A.相交或平行 B.相交或异面 C.平行或异面 D.相交，平行或异面
5. 已知直线m.n与平面α.β，给出下列三个命题：
①若
②若
③若
其中真命题的个数是
A.0
B
6. 
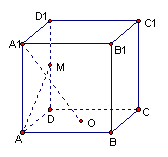如图，正方体AC1中，M是棱D1D的中点，O是正方形ABCD的中心，则异面直线OA1与AM所成的角是
A.
B.
C.
D.
7. 在平面直角坐标系中，O为坐标原点，已知两点A(3,1)、B(-1,3），若点C满足
，则点C的轨迹方程为
A.3x+2y-11=0 B.2(x -1)+2(y -2)=5
C.2 x - y =0 D.x +2 y -5=0
8.
若α是直线的倾斜角，则sin(
-α)的取值范围是
A.［-1，
］ B.(-1，) C.(-
, ) D.［-,)
9. 正方体ABCD—A1B
则动点P的轨迹是
A.线段 B.抛物线的一部分 C.双曲线的一部分 D.椭圆的一部分
10. 若一个圆的圆心在抛物线y2=4x的焦点处，且此圆与直线x+y+1=0相切，则这个圆的方程是
A.x2+y2－2x－1=0 B.x2+y2+2x+1=
第Ⅱ卷（非选择题 共5道填空题6道解答题）
请将你认为正确的答案代号填在下表中
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
二.简答题 （每小题5分，共25分）
11. 以点(1，2)为圆心，与直线4x+3y-35=0相切的圆的方程是________________.
12. 直线x+2y=0被曲线x2+y2－6x－2y－15=0所截得的弦长等于_________.
13. 设
是曲线
上的一个动点，则点到点
的距离与点到
轴的距离之和的最小值为
.
14. 直线y=k(x-2)+1
15. 设中心在原点的椭圆与双曲线
=1有公共的焦点，且它们的离心率互为倒数则该椭圆的方程是________.
三.解答题 （共75分）
16. 抛物线y＝x2上不存在关于直线y＝m(x－3)对称的两点，求m的范围。
17. 某人射击一次命中目标的概率为
。
(1)求此人射击6次恰好3次命中目标的概率。
(2)求此人射击6次至少命中2次目标的概率。
(3)(此题理科生做）求此人射击6次3次命中且恰有2次连续命中的概率。
18. 我校承办省第19届青少年科技创新大赛.布置参赛作品展时，甲展厅内有2个科技小制作系列和2个科技小论文系列，乙展厅内有2个科技小制作系列和3个科技小论文系列.现甲乙两展厅须互换一个系列.
⑴求甲展厅内恰有2个小制作系列的概率；
⑵求甲展厅内小制作系列数的期望.
19. 已知A（－2，0），B（2，0），动点P与A、B两点连线的斜率分别为
和
，且满足·=t (t≠0且t≠－1).
（１）求动点P的轨迹C的方程；
（２）当t＜0时，曲线C的两焦点为F1，F2，若曲线C上存在点Q使得∠F1QF2=120O，
求t的取值范围.
20. 皮划艇运动员甲、乙二人在相同的条件下进行了6次测试，测得他们最大速度(m／s)的数据如下：甲：27，38，30，37，35，31. 乙：33，29，38，34，28，36.根据以上数据，试判断他们谁更优秀
21. 直三棱柱ABC-A1B
BAC=900，AB=AC=2，AA
=2
，E, F分别是BC、AA1的中点。求
（1）异面直线EF和A1B所成的角。
（2）直三棱柱ABC-A1B
2008年武昌区高二数学五月段考题参考答案（仅供参考）
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| D | D | A | D | C | A | D | A | B | A |
二.简答题答案:
11. 
进制 12. 4
13. 14. 2 15. 
三.解答题答案:
16. 若m＝0，曲线y＝x2上没有关于直线y＝0对称的两点
若l与抛物线有两交点，则
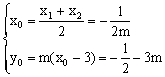
17. (1)P6（3）=
·
(2)至少命中2次的对立事件是命中1次和0次，∴P=1-P6（1）-P6（0）=1-
·
·
(3)（理）两次连续命中与另一次命中是间隔排列问题。∴
·
18. ⑴甲乙两个展厅各有一个系列交换后，甲展厅恰有2个小制作系列有下面几种情况：①两展厅交换的都是小制作系列，则此时甲展厅恰有2个小制作系列为事件A1，其概率P（A1）=
…………2分
②两展厅交换的是小论文系列，则此时甲展厅恰有2个小制系列为事件A2，其概率
P（A2）=
…………4分
故甲展厅内恰有2个小制作系列的概率为：P（A1）+ P（A2）=
………6分
⑵设甲展厅内小制作系列数为
，则的所有可能取值分别为1、2、3，
其中P（=1）=
P（=2）=
P（=3）=
∴的分布列为：
|
| 1 | 2 | 3 |
| P |
|
|
|
甲展厅内个科技小制作系列数的期望为
E=
…………12分
19. (１) 设点P坐标为(x,y),依题意得
=t
y2=t(x2－4)
+
=1
轨迹C的方程为+=1（x≠
2）.
(２) 当－1＜t＜0时，曲线C为焦点在x轴上的椭圆，
设
=r1，
= r2, 则r1+
r2=
在△F1PF2中，
=
,
∵∠F1PF2=120O，由余弦定理，
得
+r
－2r1r2
= r+r+ r1r2
= (r1+r2)2－r1r2≥(r1+r2)2－(
)2=
.
所以当－≤t＜0时，曲线上存在点Q使∠F1QF2=120O
当t＜－1时，曲线C为焦点在y轴上的椭圆，
设=r1，= r2，则r1+r2=
在△F1PF2中， =
.
∵∠F1PF2=120O，由余弦定理，得
+r－2r1r2= r+r+ r1r2= (r1+r2)2－r1r2≥(r1+r2)2－()2=
∴16（－1－t）≥－12tt≤－4.
所以当t≤－4时，曲线上存在点Q使∠F1QF2=120O
综上知当t＜0时，曲线上存在点Q使∠AQB=120O的t的取值范围是
20. 
甲＝ 
(27＋38＋30＋37＋35＋31)＝33.
乙＝(33＋29＋38＋34＋28＋36)＝33.
S*2甲＝
［(27－33)2＋(38－33)2＋(30－33)2＋(37－33)2＋(35－33)2＋(31－33)2］＝18，
S*2乙＝［(33－33)2＋(29－33)2＋(38－33)2＋(34－33)2＋(28－33)2＋(36－33)2］＝15.2.
S*2甲> S*2乙 说明二人的最大速度的平均值相同，但乙比甲更稳定，故乙比甲更优秀.
21. 
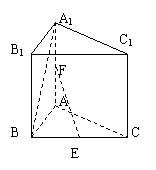（1）方法一：（略解）取AB的中点D，连DE、DF，
则
∥
，
∴∠DFE即为所求。——2分
由题意易知，
，
，
由DE⊥AB、DE⊥A A1得DE⊥平面ABB
∴△DEF为直角三角形，∠EDA=900
∴tan∠DFE=
——9分
∴
,即异面直线EF和A1B所成的角为
。——10分
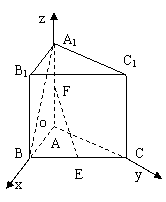方法二：
以A为坐标原点以AB、AC、
AA1所在直线分别x轴、y轴、
Z轴建立如图所示的直角坐标系，
则A (o,o,2) B (2,0,0)
E、F分别是BC、AA1中点
∴E(1,1,0) F(0,0,) ——5分
∴
设
的夹角为
∴cos=
∴ 
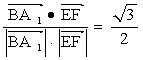
——9分
∴异面直线EF和AB所成的角为
——10分
（2）直三棱柱ABC-A1B
——13分