08年高二理科数学期中考试试卷（理科用题）
试卷满分：150分 考试时间：120分钟
命题制卷：陈建云
第Ⅰ卷
一、选择题（每小题5分，共60分。选择题答案必须做到答题卷上才有效，否则不计分）
1．条件甲：直线a、b是异面直线；条件乙：两条直线a 、b 无公共点，则甲是乙的（ ）
A．充分非必要条件 B．必要非充分条件
C．充要条件 D．既非充分又非必要条件
2．已知集合
，
，则集合A到集合B的映射个数为 （ ）
A 64 B
3．由
展开所得多项式中，系数为有理数的项共有 （ ）
A 50 B
4．A、B、C、D、E五种不同的商品要在货架上排成一排，其中A、B两种商品必须排在一起，而C、D两种商品不能排在一起，则不同的排法共有 （ ）
A．12种子 B．20种 C．24种 D．48种
5．已知棱长都相等的正三棱锥内接于一个球，某人画出四个过球心的平面截球与正三棱锥所得的图形如下，则 （ ）
A.以下四个图形都是正确的 B.只有（2）（4）是正确的
C.只有（4）是正确的 D.只有（1）（2）是正确的
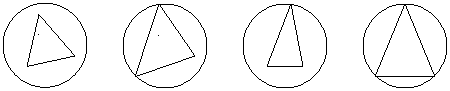
① ② ③ ④
6．四面体的顶点和各棱的中点共有10个点，在其中任取4个不共面的点，则不同的取法种数有（ ）
A
144 B
7．已知
，若
，则实数
的值为（ ）
A、1
B、－
D、
8．在下列的四个命题中：
①
是异面直线，则过分别存在平面
，使
；
②是异面直线，则过分别存在平面，使
；
③是异面直线，若直线
与都相交，则也是异面直线；
④是异面直线，则存在平面
过
且与
垂直．真命题的个数为 （ ）
A．1个 B．2个 C．3个 D．4个
9．某人制定了一项旅游计划，从7个旅游城市中选择5个进行游览.如果A、B为必选城市，并且在游览过程中必须按先A后B的次序经过A、B两城市(A、B两城市可以不相邻)，则不同的旅览线路有（ ）
A.120种 B.240种 C.480种 D.600种
10．一平面截一球得到直径是
A．
B．
C．
D．
11．在由数字1,2,3,4,5组成的所有没有重复数字的5位数中，大于23145且小于43521的数共有（ ）
A.56个 B.57个 C.58个 D.60个
12．在一个锥体中，作平行于底面的截面，若这个截面面积与底面面积之比为1∶3，则锥体被截面所分成的两部分的体积之比为 （ ）
A．1∶
B．1∶9 C．1∶
D．1∶
二、填空题（每小题4分，共16分）
13．二项式()15展开式中的常数项是第___________项.
14．在50件产品中有4件是次品，从中任抽取5件，至少有3件次品的抽法共有 __ _种（用数字作答）
15．今天是星期四,再过
天以后的第一天是星期 。（用阿拉伯数字作答）
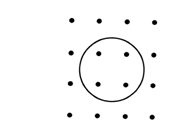
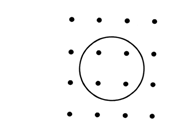
16．如图1所示，在排成4×4方阵的16个点中，中心4个点在某一圆内，其余12个点在圆外，在16个点中任选3个点构成三角形，其中至少有一个顶点在圆内的三角形共有 个.（用数字作答）
长沙外国语学校高二期中考试试卷（4-6用题）
试卷满分：150分 考试时间：120分钟
第Ⅱ卷（只交此卷）
一、选择题（每小题5分，共60分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题（每小题4分，共16分）
13、 14、 15、 16、
三、解答题(共74分,要求写出主要的证明、解答过程)
17．（10分）在北纬
圈上有甲乙两地，它们在纬度圈上的弧长为
（
为地球的半径），求：甲乙两地的球面距离为。
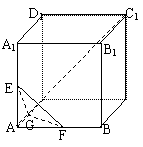18．（10分）如图，正方形ABCD-A1B
（1）求证AC1⊥平面EFG，
（2）求异面直线EF与CC1所成的角。
19．（本小题10分）求
1＋x
21－x5的展开式中x3的系数 ．
20．（14分） 4个男生,3个女生站成一排.（必须写出解析式再算出结果才能给分）
⑴ 3个女生必须排在一起,有多少种不同的排法?
⑵ 任何两女生彼此不相邻, 有多少种不同的排法?
⑶ 甲,乙二人之间恰好有三个人，有多少种不同的排法?
⑷ 甲，乙两生相邻，但都不与丙相邻，有多少种不同的排法?
21．（14分）用0 1 2 3 4 5 ，这六个数字。①可组成多少个无重复数字的五位自然数？②可组成多少个无重复数字的五位奇数？③可组成多少个无重复数字的能被5整除的五位数？④可组成多少个无重复数字的大于31250的五位数？⑤可组成多少五位偶数？ ⑥将组成的无重复数字的五位数按由小道大的顺序排列，则31250时此数列中的第几项？
22．（本小题满分12分）如图，四棱锥P—ABCD中，PB⊥底面ABCD，CD⊥PD．底面ABCD为直角梯形，AD∥BC，AB⊥BC，AB=AD=PB=3．点E在棱PA上，且PE=2EA．
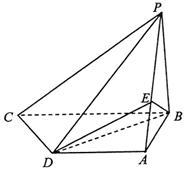（Ⅰ）求异面直线PA与CD所成的角； （Ⅱ）求证：PC∥平面EBD；
（Ⅲ）求二面角A—BE—D的大小．
长沙外国语学校高二期中考试试卷（4-6用题）答案
试卷满分：150分 考试时间：120分钟
第Ⅰ卷
一、选择题（每小题5分，共60分）
1．条件甲：直线a、b是异面直线；条件乙：两条直线a 、b 无公共点，则甲是乙的（ A ）
A．充分非必要条件 B．必要非充分条件
C．充要条件 D．既非充分又非必要条件
解：A
2．已知集合，，则集合A到集合B的映射个数为 （ A ）
A 64 B
解：注意映射的概念，分步完成
；
3．由展开所得多项式中，系数为有理数的项共有（ B
）
A
50 B
解：系数为
，为使系数为有理数，r必需为6的倍数，注意含0，故共有17项.
4．A、B、C、D、E五种不同的商品要在货架上排成一排，其中A、B两种商品必须排在一起，而C、D两种商品不能排在一起，则不同的排法共有（ ）
A．12种子 B．20种 C．24种 D．48种
解：C 将A、B捆绑在一起，再使用插入法
，
5．已知棱长都相等的正三棱锥内接于一个球，某人画出四个过球心的平面截球与正三棱锥所得的图形如下，则 （ ）
A.以下四个图形都是正确的 B.只有（2）（4）是正确的
C.只有（4）是正确的 D.只有（1）（2）是正确的
① ② ③ ④
解：D
6．四面体的顶点和各棱的中点共有10个点，在其中任取4个不共面的点，则不同的取法种数有（ D ）
A
144 B
解：间接法求解.
总情形
=210,其中四点共面的有三类:四面体的四个面的6点中任取4点有
;6个点中,4点共面的有3种取法;6个点与对棱上的3点共面,有6种取法.所以,共有不同的取法210-60—3-6=141种.
7．已知，若，则实数的值为（ C ）
A、1
B、－
D、
解：令
，得
；再令
，得
将和代入，得
所以
8．在下列的四个命题中：
①是异面直线，则过分别存在平面，使；
②是异面直线，则过分别存在平面，使；
③是异面直线，若直线与都相交，则也是异面直线；
④是异面直线，则存在平面过且与垂直．真命题的个数为 （ B
）
A．1个 B．2个 C．3个 D．4个
解：A
9．某人制定了一项旅游计划，从7个旅游城市中选择5个进行游览.如果A、B为必选城市，并且在游览过程中必须按先A后B的次序经过A、B两城市(A、B两城市可以不相邻)，则不同的旅览线路有（ D ）
A.120种 B.240种 C.480种 D.600种
解：D 析：
.
10．一平面截一球得到直径是
A． B． C． D．
解：C
11．在由数字1,2,3,4,5组成的所有没有重复数字的5位数中，大于23145且小于43521的数共有（ C ）
A.56个 B.57个 C.58个 D.60个
解：C解析：大于23145且小于43521的数有如下五种情形：
（1）万位数字为2，千位数字为4或5的数有：
个；
（2）万位数字为2，千位数字为3，且大于23145的数有：
个；
（3）万位数字为3的数有：
个；
（4）万位数字为4，千位数字为1或2的数有：个；
（5）万位数字为4，千位数字为3，且小于43521的数有：个
∴大于23145且小于43521的数有： 12+5+24+12+5=58（个）
12．在一个锥体中，作平行于底面的截面，若这个截面面积与底面面积之比为1∶3，则锥体被截面所分成的两部分的体积之比为（ D ）
A．1∶ B．1∶9 C．1∶ D．1∶
解：D
二、填空题（每小题4分，共16分）
13．二项式()15展开式中的常数项是第_____7______项.
解： Tr＋1＝C(－2x
)15－r＝C(－2)rx
，由5－＝0，得r＝6
故展开式中的常数项是第7项.
14．在50件产品中有4件是次品，从中任抽取5件，至少有3件次品的抽法共有__4186_种（用数字作答）
解：4186种 解析：对抽取5件产品中的次品分类讨论：（1）抽取的5件产品中恰好有3件次品；（2）抽取的5件产品中恰好有4件次品，于是列式如下：
=4140+46=4186
15．今天是星期四,再过天以后的第一天是星期 5
。（用阿拉伯数字作答）
解：用二项式定理，
则星期五;
16．如图1所示，在排成4×4方阵的16个点中，中心4个点在某一圆内，其余12个点在圆外，在16个点中任选3个点构成三角形，其中至少有一个顶点在圆内的三角形共有 312 个.（用数字作答）
解： 
第Ⅱ卷
一、选择题（每小题5分，共60分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题（每小题4分，共16分）
13、 14、 15、 16、
三、解答题(共74分,要求写出主要的证明、解答过程)
17．（10分）在北纬圈上有甲乙两地，它们在纬度圈上的弧长为（为地球的半径），求：甲乙两地的球面距离为。
答：
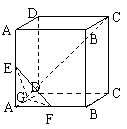
18．（10分）如图，正方形ABCD-A1B
分别是AB，AD，AA1的中点,
（1）求证AC1⊥平面EFG，
（2）求异面直线EF与CC1所成的角。
（1）解：∵E，F分别是AA1，AB的中点，∴EF//A1B
∵B1B//C
在RT⊿A1BB1中,∠ABB=45º
∴EF与CC所成的角为45º
（2）证明：
∵C1B1⊥面A1ABB1, A1B⊥AB1 由三垂线定理得AC1⊥A1B
∵EF//AB， AC1⊥EF 同理可证AC1⊥GF
∵GF与EF是平面EFG内的两条相交直线
∴AC1⊥面EFG
19．（本小题10分）求1＋x21－x5的展开式中x3的系数 ．
解法一：先变形，再部分展开，确定系数
所以x3的系数是第一个括号内的1与第二个括号内的－x3的系数－1相乘和第一个括号内的－2 x2的系数－2与第二个括号内的－3 x的系数－3相乘后再相加而得到，即1×－1+－2×－3=5
解法二：利用通项公式因
的通项公式为
的通项公式为
其中
令
则
或
或
故x3的系数为
20．（14分） 4个男生,3个女生站成一排.（必须写出解析式再算出结果才能给分）
⑴ 3个女生必须排在一起,有多少种不同的排法?
⑵ 任何两女生彼此不相邻, 有多少种不同的排法?
⑶ 甲,乙二人之间恰好有三个人，有多少种不同的排法?
⑷ 甲，乙两生相邻，但都不与丙相邻，有多少种不同的排法?
解：⑴ 先排3个女生作为一个元素与其余的4个元素做全排列有，
(种)；
⑵ 男生排好后，5个空再插女生有，
(种)；
⑶ 甲、乙先排好后，再从其余的5人中选出3人排在甲、乙之间，把排好的5个元素与最好的2个元素全排列，分步有，
(种)；
⑷ 先甲、乙相邻，再把甲乙这个整体与丙分别插入其余4个元素全排列构成的5个空位中，分步有，
(种).
21．（14分）用0 1 2 3 4 5 ，这六个数字。①可组成多少个无重复数字的五位自然数？②可组成多少个无重复数字的五位奇数？③可组成多少个无重复数字的能被5整除的五位数？④可组成多少个无重复数字的大于31250的五位数？⑤可组成多少五位偶数？ ⑥将组成的无重复数字的五位数按由小道大的顺序排列，则31250时此数列中的第几项？
解析：①解法一：直接法：C
*A
=600个，解法二：间接法： A
-A=600个。
②一个数是否为奇数取决于个位数字，所以个位为特殊位置，又0不能排在首位，所以0为特殊数字，应优先考虑，有C
* C
* A
=288个。
③可分两类：末位是0时有A个，末位是5时，首位又不能是0，有(A-A) 个，共有A+(A -A ) =216个。
④用分类法解： C
* A +C *A +C *A
+1 =325个
⑤ A +C *A * A =120+193 =312个
⑥既要找出比31250小的五位数，有C*A+A +A +A*A=240+24+6+4=274（个）。即31250是此数列中的第275项。
22．（本小题满分12分）如图，四棱锥P—ABCD中，PB⊥底面ABCD，CD⊥PD．底面ABCD为直角梯形，AD∥BC，AB⊥BC，AB=AD=PB=3．点E在棱PA上，且PE=2EA．
（Ⅰ）求异面直线PA与CD所成的角； （Ⅱ）求证：PC∥平面EBD；
（Ⅲ）求二面角A—BE—D的大小．
解：（Ⅰ）建立如图所示的直角坐标系B—xyz.
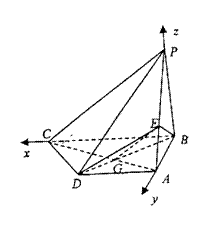
（Ⅱ）连结AC交BD于G，连结EG，
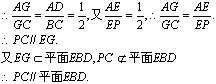
（Ⅲ）设平面BED的法向量为
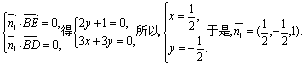
又因为平面ABE的法向量
