高二数学（文科）上册期末考试题

高二数学（文科）上册期末考试题

　　　　

一.选择题:(每小题5分,共50分)

1．已知△ABC中，a＝4，b＝4，∠A＝30°，则∠B等于(  D　)

　A．30°　 　　　　　　　　　B．30°或150°  

　C．60°　　 　　　　 　　　D．60°或120°

2．在△ABC中，AB＝5，BC＝7，AC＝8，则的值为(　D  )

　A．79　　　B．69　　　　 C．5　　 　　　 D．-5

3．在△ABC中，“A>30⁰”是“sinA>”的…………………（ B　 ）

A．充分不必要条件　　　　　　B．必要不充分条件　

 C．充要条件 　　　　　　　　 D．既不充分又不必要条件

4．若点A的坐标为（3，2），为抛物线的焦点，点是抛物线上的一动点，则 取得最小值时点的坐标是　　　　　　　　  （ C　 ）

A．（0，0） 　　　　　　　　　　　　　　　　　B．（1，1）　　　　　　　　　　　

C．（2，2） 　　　　　　　　　　　　　　　D．

5．一个命题与他们的逆命题、否命题、逆否命题这4个命题中（ C ）

A.　　  真命题与假命题的个数相同　

B.　　  真命题的个数一定是奇数

C.　真命题的个数一定是偶数　　

D.真命题的个数一定是可能是奇数，也可能是偶数

6．到两定点、的距离之差的绝对值等于6的点的轨迹　　（  D　）

A．椭圆　　　　　　　　B．线段　　　　　　　 C．双曲线　　　　 D．两条射线

7.等差数列中，，那么（　B　）

A. 　　　 B. 　　　 C. 　　　　D.  

8.若椭圆的短轴为，它的一个焦点为，则满足为等边三角形的椭圆的离心率是（ D ）

 A. 　　　　 B. 　　　　 C. 　　　　D. 　　

9．等比数列中，（　　 C　　）

A．2　　　 　　　　　　　　　　B．　　　　

  C．2或　　　　　　　　　　 D．－2或

10．已知平面内有一固定线段AB,其长度为4，动点P满足PA-PB=3,则PA的最小值为 (　D　)　　　　　　　　　　　　　　　　　　　　　　　　　　　

(A)1.5　　　　　  (B)3　　　　　  (C)0.5　　　　　　 (D)3.5

二.填空题：(每小题5分,共20分)

11．如果椭圆4x²＋y²＝k上两点间的最大距离是8，那么k等于_______________. 16

12．动点 到点 的距离比到直线 的距离小2，则动点 的轨迹方程为________________________．

13．与椭圆有相同的焦点，且两准线间的距离为的双曲线方程为______________________

14．若，则的最小值是___________. 1　　　　

高二数学（文科）上册期末考试题

　　　　 　 

一、选择题（每小题5分，共50分）

题号	1	2	3	4	5	6	7	8	9	10
答案	D	D	B	C	C	D	B	D	C	D

二、填空题（每小题5分，共20分）

11、　　　16　　　　　 12、

　

13、　 　　　 14、　　1　　　

三.解答题: （共80分）

15.（14分）已知等比数列的前n项和记为  a₃=3 , a₁₀=384.

求该数列的公比q和通项a_n

  解:　由a₁₀₌ a₃q⁷　得q⁷=128, ∴q=2 ………………………7分

又a₃=3得a₁q²=3 ∴ a₁=　　………………………10分∴ a_n=×2^n-1=3·2^n-3…………………………………14分

16．(14分)抛物线的焦点F在x轴的正半轴上，A(m，-3)在抛物线上，且AF=5,求抛物线的标准方程．

　解：设抛物线的方程为y＝2px(p>0) , …………………………2分

∵A点在抛物线上，∴（-3）² =2pm ∴m=①, ………………4分又AF=②,　　　　  …………………………9分

把①代入②可得: ………………12分∴p=1或p=9　　………………13分

∴所求的抛物线方程为………………………14分

17. (14分)如图在⊿MNG中，己知NO=GO=2，当动点M满足条件sinG-sinN=sinM时，求动点M的轨迹方程．y

　　　　　　　　　　　　　　　　 　　　　　　　　M

　　　　　　　 　　　　　　　　　　　　　　　　　　　 

　　　　　　　　　 　　　　　　　　　　　　　　　 x　　　　　　　　 

　　　　　　  　　　　　　　　　　　　 N　　O　　　G　

 解：∵sinG-sinN=sinM，

∴由正弦定理，得｜MN-MG=×4．…………………………5分

∴由双曲线的定义知,点M的轨迹是以N、G为焦点的双曲线的右支(除去与x轴的交点)．　　 …………………………10分

∴2c=4,2a=2，即c=2,a=1.

∴b²=c²-a²=3．　　　　　　  …………………………12分

∴动点M的轨迹方程为：x²-=1(x>0,且y≠0)………………14分

18.（13分）记函数f(x)=的定义域为A,　g(x)=lg[(x－a－1)(2a－x)]　(a<1) 的定义域为B.

(Ⅰ) 求A；

(Ⅱ) 若BA, 求实数a的取值范围.

解：(Ⅰ) 的定义域满足不等式2－≥0, …………………2分

得≥0, 　　x <－1或x ≥1　　　　　  …………………………6分

即A=(－∞,－1)∪[1,+ ∞)　 …………………………7分

(Ⅱ) 条件BA表明,集合B是集合A成立的充分条件,首先要求出集合B.

由(x－a－1)(2a－x)>0,　　　　　　 …………………………9分

得(x－a－1)(x－2a)<0.

∵a<1,　 ∴a+1>2a,

∴B=(2a,a+1).　　　　　　　　　 …………………………11分

∵BA, ∴2a≥1或a+1≤－1,

 即a≥或a≤－2, 而a<1,

∴≤a<1或a≤－2, 　　　　　…………………………12分

故当BA时, 实数a的取值范围是.

…………………………13分

19.（13分）已知数列满足

　　　 （I）证明：数列是等比数列；

　　　 （II）求数列的通项公式；

（I）证明：

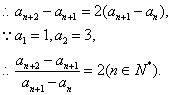
………………………7分

是以为首项，2为公比的等比数列。

……………………8分

（II）解：由（I）得……………………10分　　

　　　

　　　 　　　　　　

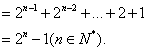
……………………………………13分

20．（12分）已知抛物线y²=4ax(0＜a＜1)的焦点为F，以A(a+4,0)为圆心，｜AF｜为半径在x轴上方作半圆交抛物线于不同的两点M和N，设P为线段MN的中点．　　　　　　　　　　　　　　　　 

（1）求｜MF｜+｜NF｜的值；

（2）是否存在这样的a值，使｜MF｜、｜PF｜、｜NF｜成等差数列?如存在，求出a的值，若不存在，说明理由.

解：（1）F（a,0）,设，由｛

，　　…………………………3分

，

　　　　　　　　　　　　　　　…………………………6分

（2）假设存在a值，使的成等差数列，

即　 ①，

　　　　　　　　　　　　　  ………………………8分

∵P是圆A上两点M、N 所在弦的中点，∴，　 …………………………10分

由①得：

，

这是不可能的．　　　　　　　 …………………………11分

∴假设不成立．即不存在a值，使的成等差数列．

　　　　　　　　　　　　　　 …………………………12分