高二理科数学第一学期期末考试

高二理科数学第一学期期末考试

高二（理科）数学试题

本试卷共150分，120分钟完成，答案写在答题卷上。

第Ⅰ卷

一、　　　　　 选择题 (本大题共8小题，每小题5分，共40分)

1、设集合，则等于（　　　）　

A.{1，2}　　　　　 B. {3，4}　　　　  C.{1}　　　　　  D. {-2，-1，0，1，2}

2、一粒骰子，抛掷一次，奇数向上的概率是（　　　）

A. 　　　　　　 B.　　　　　　  C.　　　　　  D.

3、要完成下列两项调查：①从某社区125户高收入家庭、280户中等收入家庭、95户低收入家庭中选出100户调查社会购买力的某项指标；②某中学的15名艺术特长生中选出3人调查学习负担情况。宜采用的抽样方法依次为（　　　）　　　　　　　　　　　　　　　　　　　　　　　

　　 A．①用随机抽样法，②用系统抽样法　　　　　B．①用分层抽样法，②用随机抽样法

C．①用系统抽样法，②用分层抽样法　　　D．①②都用分层抽样法

4、若椭圆上一点P到焦点F₁的距离等于6，则点P到另一个焦点F₂的距离是（　　）

A．4　　　　　  B．194　　　　　　 C．94　　　　　　　  D．14　

5、下列函数既是奇函数，又在区间上单调递减的是（　　　）

A.　 B.　 C.　D.

6、在下列关于直线、与平面、的命题中,真命题是（　　　）

　A.若且,则　　B.若且,则.

C.若且,则　　 D. 若且,则.

7、已知三角形的内角分别是A、B、C，若命题命题，则P是Q的（　　  ）

　　　　　　　　 A．充分而不必要条件　　　　　　　B．必要而不充分条件

C．充要条件　　 　　　　　　　　　  D．既不充分也不必要条件

8、.如图，第n个图形是由正n+2边形“扩展”而来，(n=1、2、3、…)则在第n个图形中

共有（　　　）个顶点.

 

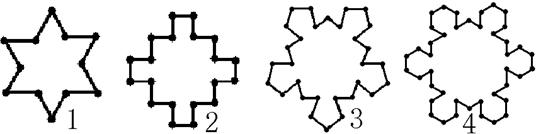
A．(n+1)(n+2)　　　　B. (n+2)(n+3)　　　　 C. 　　　 D. n

第Ⅱ卷

二、填空题（本大题共6小题每小题5分，共30分；把答案填在答题卷中相应的横线上）

9、某班5次数学测验中，甲、乙两同学的成绩如下：

甲：90　 92　 88　 92　 88　　 乙：94　 86　 88　 90　 92

则甲、乙两人成绩相比较，得出结论是　　　　　　  稳定．

10、在等差数列{a_n}中，前15项的和S₁₅＝90，则a₈＝　 　　　　　 。

11、在条件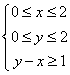下， 则的最大值是　　　　　　  。

12、某种汽车购买时费用为14．4万元，每年应交付保险费、养路费及汽油费共0.9万元，汽车的维修费为：第一年0.2万元，第二年0.4万元，第三年0.6万元，……，依等差数列逐年递增．则这种汽车使用　　　　　　  年报废最合算（即该车使用多少年平均费用最少）？

13、如果上述程序运行的结果为S=132，那么

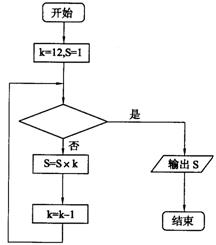
判断框中应填入　　　　　　  。

14、下列两道题任选一道题做：(若两题都做，按（甲）题答案给分)

（甲）直角三角形ABC中(C为直角),

CDAB,DEAC,DFBC,

则=　　　　　　  。

（乙）点P(x,y)为椭圆上的动点,

则2x+y的最大值为　　　　　　  。

三、解答题：（本大题共6小题，共80分.解答应写出文字说明，证明过程或演算步骤.）

15、（本小题满分12分）

已知f (x)＝·－1，其中向量＝（sin2x，cosx），＝（1，2cosx）（x∈R）

　⑴求f (x)的单调递增区间；

⑵在△ABC中，角A、B、C的对边分别为a、b、c，f (A)＝2，a＝，b＝3，求边长c的值。

16、（本小题满分14分）

数列{a_n}是公比为q的等比数列，a₁＝1，a_n+2＝ （n∈N^*）

⑴求{ a_n }的通项公式；

⑵令b_n＝n a_n，求{b_n }的前n项和S_n。

17、（本小题满分14分）

如图,在三棱锥S-ABC中，平面SAC⊥平面ABC，且△SAC是正三角形, △ABC是等腰直角三角形，其中AC=CB=2a，O是AC的中点.

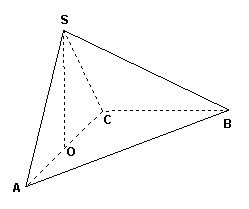(1) 求证:SO⊥AB;

(2) 求二面角B-SA-C的大小的正切值.

　　　　　　　 

18、（本小题满分14分）

某工厂可以用两种不同原料生产同一种产品，若采用甲原料，每吨成本1000元，运费500元，可得产品90千克；若采用乙种原料，每吨成本1500元，运费400元，可得产品100千克。现在预算每日总成本不得超过6000元，运费不得超过2000元，问此工厂每日最多可生产多少千克产品？

19、（本小题满分14分）

如图，点A、B分别是椭圆的长轴的左、右端点，F为椭圆的右焦点，直线PF的方程为且PA⊥PF。

⑴求直线PA的方程；

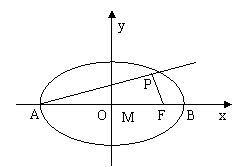⑵设M是椭圆长轴AB上的一点，M到直线AP的距离等于│MB│，求椭圆上的点到点M的距离d的最小值。

20. (本题满分12分)

已知，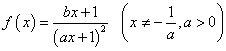

⑴求函数的表达式；

⑵定义数列，求数列的通项；

⑶求证：对任意的有.