（4）不等式
一、选择题（本大题共10小题，每小题5分，共50分）
1．已知c<d, a> b >0, 下列不等式中必成立的一个是 （ ）
A．a +c> b +d B．a -c> b -d C．a d< b c D． 
2．设a、b∈R，且a b<0，则 （ ）
A． a +b> a -b B． a +b< a -b C． a -b< a -b D． a -b< a +b
3．已知命题p:“x> a”，q:“x≥a”，则p是q的 （ ）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．非充分非必要条件
4．不等式 x -4≤3 的整数解的个数是 （ ）
A．7 B．
5．设集合p={ x -2< x <3}，Q={ x x +1>2，x∈R}，则集合P∪Q= （ ）
A．{ x -2< x <1} B．{ x 1< x <3}
C．{ x -3< x <3 D．{ x x <-3 或x >-2}
6．若log
A．4 B．
D．9
7．不等式
的解集是 （ ）
A．(-3, -2)∪(0, +∞) B．(-∞, -3)∪(-2, 0)
C．(-3, 0) D．(-∞, -3)∪(0, +∞)
8．若a < b <0，则下列结论中正确的是 （ ）
- 不等式
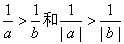均不成立 - 不等式
均不成立 - 不等式
均不成立 - 不等式
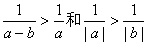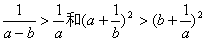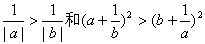均不成立
9．关于x的不等式a x 2+b x
+2>0的解集是
，则a +b= （ ）
A．10 B．
10．已知集合A={ x x -1≤a, a >0}, B={ x x -3>4}，且A∩B=φ，则a的取值范围是
（ ）
A．(0, 2] B．(-∞, 2] C．(7, +∞) D．(- ∞, -1)
二、填空题（本大题共4小题，每小题6分，共24分）
11．已知sin2α+sin2β+sin2r=1(α、β、r均为锐角)，则cosαcosβcosr的最大值等于 ．
12．若扇形的面积为S，则半径是 时扇形的周长最小．
13．不等式
的解集是
.
14．某工厂建造一间地面面积为
三、解答题（本大题共6题，共76分）
15．已知0 < x
< 1, 0 < a < 1，试比较
的大小．（12分）
16．解不等式
．（12分）
17．锐角三角形△ABC中，已知边a =1，b=2，求边c的取值范围．（12分）
18．求证：
（12分）
19．已知
当a¹b时 求证：
．（14分）
20．从社会效益和经济效益出发，某地投入资金进行生态环境建设，并以此发展旅游产业，根据规划，本年度投入800万元，以后每年投入比上年减少
．本年度当地旅游业收入估计为400万元，由于该项建设对旅游业的促进作用，预计今后的旅游业收入每年会比上年增加
（Ⅰ）设n年内（本年度为第一年）总投入为a n万元，旅游业总收入为b n万元．写出a n，b n的表达式；
（Ⅱ）至少经过几年旅游业的总收入才能超过总投入？ （14分）
参考答案
一．选择题（本大题共10小题，每小题5分，共50分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | B | A | A | D | B | A | B | D | A |
二．填空题（本大题共4小题，每小题6分，共24分）
11．
12．
13．
14．34600
三、解答题（本大题共6题，共76分）
15．（12分）
[解法一]：
∵0 < 1 - x2 < 1, 
∴
∴
[解法二]：
∵0 < 1 - x2 < 1, 1
+ x > 1, ∴
∴
∴
[解法三]：∵0 < x < 1, ∴0 < 1 - x < 1, 1 < 1 + x < 2,
∴
∴左 - 右 = 
∵0 < 1 - x2 < 1, 且0 < a < 1 ∴
∴
16．（12分）
[解析]：原不等式可化为：
即：
解之得：
或
∴x>2或
∴不等式的解集为{xx>2或}
17．（12分）
[解析]：因为△ABC是锐角三角形，且a=1，b=2，c>0， 所以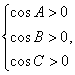
即，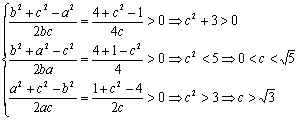
因此，所求c的取值范围是（
）
18．（12分）
[证法一]： 当
时，不等式显然成立，
当
时，由
所以，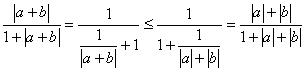
[证法二]：要证明原不等式成立，则只需证明：
a+b(1+a)(1+b)≤a(1+a+b)(1+b)+b(1+a+b)(1+a),
展开，合并同类项，得：a+b≤a+2ab+a2b+ab2+b,
∵a+b≤a+b, ∴a+b≤a+2ab+a2b+ab2+b成立，
故原不等式成立．
19．（14分）
[证法一]：
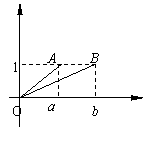[证法二]：（构造法）
如图：
由三角形两边之差小于第三边得：
20．（14分）
[解析]：（Ⅰ）第1年投入为800万元，第2年投入为800×（1-
）万元，．．．．．．，第n年投入为800×
万元．
所以，n年内的总投入为
第1年旅游业收入为400万元，第2年旅游业收入为400×
万元．．．．．．．，第n年旅游业收入为400×
万元．
所以，n年内的旅游业总收入为
（Ⅱ）设至少经过n年旅游业的总收入才能超过总投入，由此
即
-
>0
化简得
+
-7>0
设
，得5 x 2-7 x +2>0，解之得
（不合题意，舍去）
即 
由此得 
答：至少经过5年旅游业的总收入才能超过总投入．